山东省济南市莱芜区2023-2024学年八年级上学期期中考试数学试题（五四学制）

试卷更新日期：2023-12-28 类型：期中考试

进入出卷网下载

一、选择题（本大题共10个小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的.）

1. 下列从左到右的运算是因式分解的是（）

A、 ${(a b)}^{2} - 1 = (a b + 1) (a b - 1)$ B、 $(a - b) (a + b) = a^{2} - b^{2}$ C、 $a^{2} + b^{2} = {(a - b)}^{2} + 2 a b$ D、 $2 a^{2} - 2 a + 1 = 2 a (a - 1) + 1$

查看试题解析
2. 下列各式是最简分式的是（）

A、 $\frac{4}{2 x}$ B、 $\frac{x + y}{x^{2} - y^{2}}$ C、 $\frac{2 x}{x + 2}$ D、 $\frac{x^{2}}{x y}$

查看试题解析
3. 将分式 $\frac{x y^{2}}{x + y}$ 中的 $x$ ， $y$ 的值同时扩大为原来的3倍，则分式的值（）

A、扩大6倍 B、扩大3倍 C、不变 D、扩大9倍

查看试题解析
4. 某同学对数据27，38，38，49，5■，53进行统计分析，发现其中一个两位数的个位数字被墨水涂污看不到了，则计算结果与被涂污数字无关的是（）

A、平均数 B、中位数 C、方差 D、众数

查看试题解析
5. 若 $4 x^{2} + (k + 1) x + 9$ 能用完全平方公式因式分解，则 $k$ 的值为（）

A、 $\pm 6$ B、 $\pm 12$ C、 $- 13$ 或11 D、13或 $- 11$

查看试题解析
6. 关于 $x$ 的方程 $\frac{x + 1}{x - 1} = \frac{m}{1 - x} - 1$ 有增根，则 $m$ 的值是（）

A、2 B、0或2 C、 $- 2$ D、 $\pm 2$

查看试题解析
7. 甲、乙两班举行电脑汉字输入速度比赛，参赛学生每分钟输入汉字的个数经统计后的结果如表：
班级
参加人数
中位数
方差
平均数
甲
55
148
192
135
乙
55
151
110
135
某同学根据表中数据分析得出下列结论：
①甲、乙两班学生成绩的平均水平相同；
②乙班优秀的人数多于甲班优秀的人数；（每分钟输入汉字≥150个为优秀）；
③甲班成绩的波动情况比乙班成绩的波动小.
上述结论中正确的是（）

A、（1）（2）（3） B、（1）（2） C、（1）（3） D、（2）（3）

查看试题解析
8. 下列各式的分解因式：
① $64 m^{2} - 9 n^{2} = (8 m + 3 n) (8 m - 3 n)$ ；② $- 9 a^{2} - b^{2} = - (3 a + b) (3 a - b)$ ；
③ $x^{2} - 10 = (x - 5) (x + 2)$ ；④ $- 4 x^{2} - 4 x + 1 = - {(2 x - 1)}^{2}$ .
其中正确的个数有（）

A、1 B、2 C、3 D、0

查看试题解析
9. 一组数据 $a$ 、 $b$ 、 $c$ 、 $d$ 、 $e$ 、 $f$ 、 $g$ 的平均数是 $m$ ，方差是 $n$ ，则另一组数据 $3 a - 2$ 、 $3 b - 2$ 、 $3 c - 2$ 、 $3 d - 2$ 、 $3 e - 2$ 、 $3 f - 2$ 、 $3 g - 2$ 的平均数和方差分别是（）

A、3， $3 n - 2$ B、 $3 m - 2$ ， $n$ C、 $m - 2$ ， $3 n$ D、 $3 m - 2$ ， $9 n$

查看试题解析
10. 当 $x$ 分别取 $- 2024 ， - 2023 ， - 2022 ， - 2021 ， \dots ， - 3 ， - 2 ， - 1，1 ， \frac{1}{2} ， \frac{1}{3} ， \dots ， \frac{1}{2021} ， \frac{1}{2022} ， \frac{1}{2023} ， \frac{1}{2024}$ 时，分别计算分式 $\frac{x^{2} - 1}{x^{2} + 1}$ 的值，再将所得结果相加，其和等于（）

A、 $- 1$ B、0 C、1 D、2023

查看试题解析

二、填空题（本大题共6个小题，每小题4分，共24分.请直接填写答案.）

11. 分解因式： $m^{3} - 3 m^{2} =$ .

查看试题解析
12. 数据2， $x$ ， 4，2，8，5的平均数为6，这组数据的极差为.

查看试题解析
13. 关于 $x$ 的方程 $\frac{m}{x - 1} + \frac{3}{1 - x} = 2$ 的解为非负数，则 $m$ 的取值范围为.

查看试题解析
14. 甲、乙两个同学因式分解 $x^{2} + a x + b$ 时，甲看错了 $b$ ，分解结果为 $(x + 4) (x - 8)$ ，乙看错了 $a$ ，分解结果为 $(x - 2) (x + 6)$ .则 $a =$ ， $b =$ .

查看试题解析
15. 对于任意两个非零实数 $a$ 、 $b$ ，定义新运算“*”如下： $a * b = \frac{1}{b} - \frac{1}{a}$ ，例如： $3 * 4 = \frac{1}{4} - \frac{1}{3} = - \frac{1}{12}$ .若 $x * y = 2$ ，则 $\frac{2023 (x - y)}{x y =}$ .

查看试题解析
16. 取5张看上去无差别的卡片，分别在正面写上数字： $- 1$ ， 1， $- 2$ ， 2， $- 3$ ， 3，现把它们洗匀正面朝下，随机摆放在桌面上.从中任意抽出1张，记卡片上的数字为 $m$ ，则数字 $m$ 使分式方程 $\frac{x - m}{x - 2} + \frac{1}{x} = 1$ 无解的概率为.

查看试题解析

三、解答题（本大题共10小题，共86分，解答应写出文字说明，证明过程或演算步骤.）

17. 因式分解：

(1)、 $a^{2} (a - b) + b^{2} (a - b)$

(2)、 ${(m^{2} + 1)}^{2} - 4 m^{2}$

查看试题解析
18. 解分式方程：

(1)、 $\frac{3}{x + 1} = \frac{1}{x - 1}$

(2)、 $\frac{x}{x - 2} - 1 = \frac{2}{(x - 1) (x - 2)}$

查看试题解析
19. 某校八年级学生在一次射击训练中，随机抽取10名学生的成绩如下表，请回答问题：
环数
6
7
8
9
人数
1
5
3
$m$

(1)、填空：10名学生的射击成绩的众数是，中位数是， $m =$ ；

(2)、求这10名学生的平均成绩；

查看试题解析
20. 先化简，后求值： $(\frac{1}{x - 1} - 1) \div \frac{x^{2} - 4 x + 4}{x - 1}$ ，然后在0，1，2三个数中选一个适合的数，代入求值.

查看试题解析
21. 已知： $A = x^{2} - 1$ ， $B = x^{2} y^{3} - x y^{3}$ ， $C = (x + 1) (x - 3) + 4$ ，问多项式 $A$ 、 $B$ 、 $C$ 是否有公因式？若有，求出其公因式；若没有，请说明理由.

查看试题解析
22. 某政府计划对全县中小学多媒体教室进行安装改造，现安排两个安装公司共同完成.已知甲公司安装工效是乙公司安装工效的1.5倍，乙公司安装96间教室比甲公司安装同样数量的教室多用8天.

(1)、求甲、乙两个公司每天各安装多少间教室？

(2)、已知甲公司安装费每天1400元，乙公司安装费每天800元，现需安装教室100间，若想尽快完成安装工作且安装总费用不超过22600元，则最多安排甲公司工作多少天？

查看试题解析
23. 若干块正方形和长方形卡片如图1所示，其中甲型、乙型卡片分别是边长为 $a$ ， $b$ （ $a > b$ ）的正方形，丙型卡片是长为 $a$ 、宽为 $b$ 的长方形，选取2块甲型卡片，2块乙型卡片，5块丙型卡片，拼成如图2所示的大长方形卡片.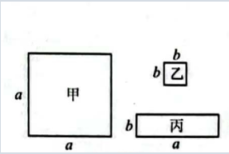

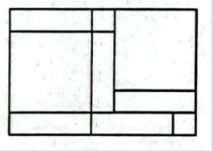
图1 图2

(1)、观察图2，写出一个多项式的因式分解为：；

(2)、若图2中甲型、乙型卡片的面积和为80，大长方形卡片的周长为48，求大长方形卡片的面积.

查看试题解析
24. 为提高学生学习数学的兴趣，培养学生的数学运算能力，某学校初一级部举行了一次“数学运算能力大比拼”活动，随机抽取两个班（不妨记做甲班、乙班），对某次数学成绩进行了统计.已知抽取的两个班的人数相同，把所得数据绘制成如下统计图表.根据图表提供的信息，回答下列问题：
组别
分数
人数
$A$
$x < 30$
2
$B$
$30 \leq x < 60$
4
$C$
$60 \leq x < 90$
$m$
$D$
$90 \leq x < 120$
38
$E$
$120 \leq x \leq 150$
27
甲乙两班数学成绩统计表

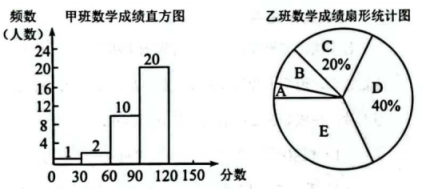(1)、样本中，乙班学生人数是人：扇形统计图中， $E$ 组对应的圆心角度数是；

(2)、 $m =$ ，请补全频数分布直方图；

(3)、样本中，甲班数学成绩的众数在组，中位数在组；

(4)、本次数学考试成绩得分在90分（含90）以上为合格，已知初一级部共有540名学生，请估计初一级部本次数学考试成绩合格人数约有多少人？

查看试题解析
25. 阅读材料：利用公式法，可以将一些形如 $a x^{2} + b x + c (a \neq 0)$ 的多项式变形为 $a {(x + m)}^{2} + n$ 的形式，我们把这样的变形方法叫做多项式 $a x^{2} + b x + c (a \neq 0)$ 的配方法，运用多项式的配方法及平方差公式能对一些多项式进行因式分解.
例如：
$x^{2} + 4 x - 5 = x^{2} + 4 x + {(\frac{4}{2})}^{2} - {(\frac{4}{2})}^{2} - 5 = {(x + \frac{4}{2})}^{2} - 4 - 5 = (x + 2)^{2} - 9$
$= (x + 2 + 3) (x + 2 - 3) = (x + 5) (x - 1)$ .
根据以上材料，解答下列问题.

(1)、分解因式： $x^{2} - 2 x - 3$ ；

(2)、求多项式 $x^{2} + 6 x - 10$ 的最小值；

(3)、已知 $a$ ， $b$ ， $c$ 是 $△ A B C$ 的三边长，且满足 $a^{2} + b^{2} + c^{2} + 70 = 6 a + 12 b + 10 c$ ，求 $△ A B C$ 的周长.

查看试题解析
26. 中秋节是我国的传统节日，人们素有吃月饼的习俗.某超市节前打算购进甲、乙两种畅销口味的月饼，已知甲种月饼每箱的进价比乙种月饼每箱的进价多16元，用4200元购进甲种月饼和用2800元购进乙种月饼的数量相同.

(1)、甲种月饼每箱的进价和乙种月饼每箱的进价各是多少元？

(2)、商店计划用不超过7680元的资金购进甲、乙两种月饼共200箱，其中甲种月饼的数量不低于乙种月饼数量的 $\frac{3}{5}$ ，该商店有几种进货方案？（不用写出具体方案）

(3)、若商店将甲种月饼每箱售价定为78元，乙种月饼每箱售价定为48元，在（2）的条件下，商品全部售出，哪种进货方案获利最大？最大利润为多少元？

查看试题解析

班级	参加人数	中位数	方差	平均数
甲	55	148	192	135
乙	55	151	110	135

组别	分数	人数
$A$	$x < 30$	2
$B$	$30 \leq x < 60$	4
$C$	$60 \leq x < 90$	$m$
$D$	$90 \leq x < 120$	38
$E$	$120 \leq x \leq 150$	27