广东省佛山市顺德区2023-2024学年高三上学期12月月考数学试题
试卷更新日期:2023-12-28 类型:月考试卷
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 设集合 , ,则 ( )A、 B、 C、 D、2. 人们对数学研究的发展一直推动着数域的扩展,从正数到负数、从整数到分数、从有理数到实数等等.16世纪意大利数学家卡尔丹和邦贝利在解方程时,首先引进了 , 17世纪法因数学家笛卡尔把i称为“虚数”,用表示复数,并在直角坐标系上建立了“复平面”.若复数z满足方程 , 则( )A、 B、 C、 D、3. 我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先成果,哥德巴赫猜想如下:每个大于2的偶数都可以表示为两个素数(一个整数除了1和它本身没有其他约数的数称为素数)的和,如 , 在不超过25的素数中,随机选取2个不同的数,则这2个数恰好含有这组数的中位数的概率是( )A、 B、 C、 D、4. 设平面向量 , , 且 , 则=( )A、1 B、14 C、 D、5. 是两个平面,m,n是两条直线,则下列四个选项错误的是( )A、如果 ,那么 . B、如果 , 那么 . C、如果 , 那么 . D、如果 , 那么 与 所成的角和 与 所成的角相等.6. 设 , , 且 , 则( )A、 B、 C、 D、7. 已知双曲线C:的焦点到渐近线的距离为 , 直线l与C相交于A、B两点,若线段的中点为 , 则直线l的斜率为( )A、 B、1 C、 D、28. 设 , , , 则( )A、 B、 C、 D、
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
-
9. 设为两个互斥的事件,且 , 则( )A、 B、 C、 D、10. 已知函数 , 则下列说法正确的是( )A、为函数图象的一条对称轴. B、函数在上单调递减. C、将的图象向右平移个单位,得到函数的图象,若在上的最小值为 , 则m的最大值为 . D、在上有2个零点,则实数a的取值范围是 .11. 如图,在棱长为的正方体中,点在线段(不包含端点)上,则下列结论正确的有( )个
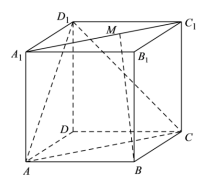 A、点在平面的射影为的中心; B、直线平面; C、异面直线与所成角不可能为; D、三棱锥的外接球表面积的取值范围为 .12. 已知定义在上的函数可导,且不恒为为奇函数,为偶函数,则( )A、的周期为4 B、的图象关于直线对称 C、 D、
A、点在平面的射影为的中心; B、直线平面; C、异面直线与所成角不可能为; D、三棱锥的外接球表面积的取值范围为 .12. 已知定义在上的函数可导,且不恒为为奇函数,为偶函数,则( )A、的周期为4 B、的图象关于直线对称 C、 D、三、填空题:本题共4小题,每小题5分,共20分.
-
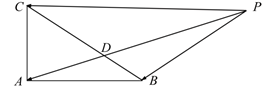
13. 的展开式中,常数项是.14. “中国剩余定理”又称“孙子定理”,可见于中国南北朝时期的数学著作《孙子算经》卷下第十六题的“物不知数”问题,原文如下:今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二.问物几何?现有一个相关的问题:将1到2 023这2 023个自然数中被3除余2且被5除余4的数按照从小到大的顺序排成一列,构成一个数列,则该数列的项数为 .15. 已知椭圆的左焦点为F,过原点O的直线l交椭圆C于点A,B,且 , 若 , 则椭圆C的离心率是 .16. 在△ABC中, D在边BC上,延长AD到P,使得AP=9,若 (m为常数),则CD的长度是 .
四、解答题:本题共6小题,共70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.
-
17. 记的内角A,B,C的对边分期为a,b,c,已知点D在边AC上,且 , .(1)、证明:是等腰三角形;(2)、若 , 求18. 已知数列 , 满足 , , .(1)、证明: 是等比数列;(2)、求数列 的前 项和 .19. 如图,已知四棱台的上、下底面分别是边长为2和4的正方形, , 且底面 , 点分别在棱、上·
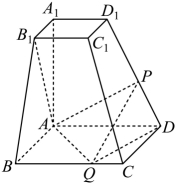 (1)、若P是的中点,证明:;(2)、若平面 , 且平面PQD与平面AQD的夹角的余弦值为 , 求四面体的体积.20. 设有甲、乙、丙三个不透明的箱子,每个箱中装有除颜色外都相同的5个球,其中甲箱有3个蓝球和2个黑球,乙箱有4个红球和1个白球,丙箱有2个红球和3个白球.摸球规则如下:先从甲箱中一次摸出2个球,若从甲箱中摸出的2个球颜色相同,则从乙箱中摸出1个球放入丙箱,再从丙箱中一次摸出2个球;若从甲箱中摸出的2个球颜色不同,则从丙箱中摸出1个球放入乙箱,再从乙箱中一次摸出2个球.(1)、若最后摸出的2个球颜色不同,求这2个球是从丙箱中摸出的概率;(2)、若摸出每个红球记2分,每个白球记1分,用随机变量表示最后摸出的2个球的分数之和,求的分布列及数学期望.
(1)、若P是的中点,证明:;(2)、若平面 , 且平面PQD与平面AQD的夹角的余弦值为 , 求四面体的体积.20. 设有甲、乙、丙三个不透明的箱子,每个箱中装有除颜色外都相同的5个球,其中甲箱有3个蓝球和2个黑球,乙箱有4个红球和1个白球,丙箱有2个红球和3个白球.摸球规则如下:先从甲箱中一次摸出2个球,若从甲箱中摸出的2个球颜色相同,则从乙箱中摸出1个球放入丙箱,再从丙箱中一次摸出2个球;若从甲箱中摸出的2个球颜色不同,则从丙箱中摸出1个球放入乙箱,再从乙箱中一次摸出2个球.(1)、若最后摸出的2个球颜色不同,求这2个球是从丙箱中摸出的概率;(2)、若摸出每个红球记2分,每个白球记1分,用随机变量表示最后摸出的2个球的分数之和,求的分布列及数学期望.