广东省深圳市教育集团2023-2024学年高一上学期第二阶段考试数学试题
试卷更新日期:2023-12-28 类型:期中考试
一、单项选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1. 已知全集 , 集合 , , 则( )A、 B、 C、 D、2. 设 , 不等式的一个充分不必要条件是( )A、 B、 C、 D、3. 若幂函数的图象不经过原点,则b的值为( )A、 B、 C、 D、4. 二次函数在上的最大值为( )A、-1 B、0 C、3 D、45. 函数的大致图象是( )A、
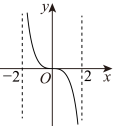 B、
B、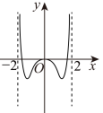 C、
C、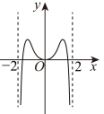 D、
D、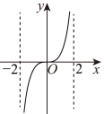 6. 若正数满足 , 则的最小值为( )A、 B、 C、12 D、167. 若实数 , 函数在R上是单调递增函数,则的取值范围为( )A、 B、 C、 D、8. 已知函数 , 若对 , , 使得 , 则的取值范围是( )A、 B、 C、 D、
6. 若正数满足 , 则的最小值为( )A、 B、 C、12 D、167. 若实数 , 函数在R上是单调递增函数,则的取值范围为( )A、 B、 C、 D、8. 已知函数 , 若对 , , 使得 , 则的取值范围是( )A、 B、 C、 D、二、多项选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,有选错的得0分,部分选对的得2分。
-
9. 下列各组函数中,表示同一函数的是( )A、 , B、 , C、 , D、 ,10. 已知函数是定义在上的偶函数,且对任意的 , 总有 , 则下列结论正确的是( )A、 B、 C、 D、11. 已知正实数满足 , 则下列结论中正确的是( )A、若 , , 则 B、若 , , 则 C、若 , , 则 D、若 , , 则12. 已知函数 , , 函数在区间上的最大值为9,最小值为1.函数与函数图象在上有两个不同的交点,则实数的可能取值为( )A、0 B、 C、 D、1
三、填空题:本题共4小题,每小题5分,共20分。
-
13. 已知函数 , 若函数的定义域为 , 则实数的取值范围是.14. 已知 , 若 , 则的值为.15. 已知 , , 且 , 则的最小值为 .16. 设函数的定义域为 , 且对任意实数恒有:
①;②;③当时,.
若在上恰有三个零点,则的取值范围为 .
四、解答题: 本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
-
17.(1)、化简求值:(2)、已知 , 且 , 求的值.18. 已知为定义在R上的偶函数,当时,.
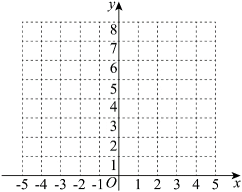 (1)、用分段函数表示时的解析式,作出在定义域内的图象,并指出的值域;(2)、讨论直线与图象的交点个数(不需证明).19. 设命题 , 不等式恒成立;
(1)、用分段函数表示时的解析式,作出在定义域内的图象,并指出的值域;(2)、讨论直线与图象的交点个数(不需证明).19. 设命题 , 不等式恒成立;命题 , 使成立.
(1)、若p为真命题,求实数m的取值范围;
(2)、若命题p、q至多有一个是真命题,求实数m的取值范围.20. 在国家大力发展新能源汽车产业政策影响下,我国新能源汽车的产销量高速增长.某地区2019年底新能源汽车保有量为1500辆,2020年底新能源汽车保有量为2250辆,2021年底新能源汽车保有量为3375辆.
(1)、根据以上数据,试从和两种函数模型中选择一个最恰当的模型来刻画新能源汽车保有量的增长趋势并说明理由,设从2019年底起经过x年后新能源汽车保有量为y辆,求出新能源汽车保有量y关于x的函数关系式;
(2)、2019年底该地区传统能源汽车保有量为50000辆,且传统能源汽车保有量每年下降2%,若每年新能源汽车保有量按(1)中求得的函数模型增长,试估计到哪一年底新能源汽车保有量将超过传统能源汽车保有量.(参考数据:)