黑龙江省牡丹江市名校2023-2024学年高三上学期第三次月考数学试卷

试卷更新日期：2023-12-27 类型：月考试卷

进入出卷网下载

一、单项选择题（共8小题，每小题5分，每题只有一个正确选项，共40分）

1. 已知集合 $M = \{y |- 1 < y < 3 \}$ ， $N = \{x |x (2 x - 9) < 0 \}$ ，则 $M \cup N =$ （）

A、 $(0 ， 3)$ B、 $(0 ， \frac{9}{2})$ C、 $(- 1 ， \frac{9}{2})$ D、 $\emptyset$

查看试题解析
2. 若 $z （ 1 + i ） = i$ （其中 $i$ 为虚数单位），则 $| z |$ 等于（）

A、1 B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{1}{2}$

查看试题解析
3. 在 $△ A B C$ 中， $\vec{B D} = \frac{3}{4} \vec{B C}$ ，点 $P$ 在线段 $A D$ 上（ $P$ 不与 $A ， D$ 点重合）， $\vec{B P} = m \vec{B A} + \frac{1}{2} \vec{B C}$ ，则实数 $m =$ （）

A、 $- \frac{2}{3}$ B、 $- \frac{1}{6}$ C、 $\frac{1}{3}$ D、 $\frac{5}{6}$

查看试题解析
4. 已知 $S_{n}$ 是各项均为正数的等比数列 $\{a_{n}\}$ 的前 $n$ 项和， $a_{7} =64$ ， $a_{1} a_{5} + a_{3} =20$ ，则 $S_{5} =$ （）

A、31 B、63 C、16 D、127

查看试题解析
5. 生物入侵是指生物由原生存地侵入到另一个新的环境，从而对入侵地的生态系统造成危害的现象.若某入侵物种的个体平均繁殖数量为Q，一年四季均可繁殖，繁殖间隔T为相邻两代间繁殖所需的平均时间.在物种入侵初期，可用对数模型 $K (n) = λ l n n$ （ $λ$ 为常数）来描述该物种累计繁殖数量 $n$ 与入侵时间K（单位：天）之间的对应关系，且 $Q = \frac{T}{λ} + 1$ ，在物种入侵初期，基于现有数据得出 $Q = 6$ ， $T = 50$ .据此估计该物种累计繁殖数量比初始累计繁殖数量增加11倍所需要的时间为（ $l n 2 \approx 0.69$ ， $l n 3 \approx 1.10$ ）（）

A、22.0天 B、13.8天 C、24.8天 D、17.9天

查看试题解析
6. 在边长为 $2$ 的菱形 $A B C D$ 中， $∠ B A D = 60^{\circ} ， E$ 为 $C D$ 的中点，则 $\overset{⃑}{A E} \cdot \overset{⃑}{B D}$ 的值为

A、 $1$ B、 $\sqrt{3}$ C、 $\sqrt{5}$ D、 $\sqrt{7}$

查看试题解析
7. 在 ${（ x - 2 ）}^{6}$ 展开式中，二项式系数的最大值为 $a$ ，含 $x^{5}$ 项的系数为 $b$ ，则 $\frac{a}{b} =$

A、 $\frac{5}{3}$ B、 $- \frac{5}{3}$ C、 $\frac{3}{5}$ D、 $- \frac{3}{5}$

查看试题解析
8. 设 $a = {l o g}_{4} 8 ， b = 2 l n 2 ， c = \frac{2}{3^{x} + 1} + \frac{2}{3^{- x} + 1}$ ，则（）

A、 $c > a > b$ B、 $a > c > b$ C、 $b > a > c$ D、 $b > c > a$

查看试题解析

二、多选题（共4小题，每小题5分，每题有多个正确选项，选不全得2分，选错得0分，完全正确得5分，共20分）

9. 记 $S_{n}$ 为等差数列 $\{a_{n}\}$ 的前n项和 $.$ 若 $a_{4} + a_{5} = 24$ ， $S_{6} = 48$ ，则下列正确的是（）

A、 $a_{1} = - 2$ B、 $d = - 4$ C、 $a_{n} = 4 n - 6$ D、 $S_{n} = 2 n^{2} - 4 n$

查看试题解析
10. 已知向量 $\vec{a}$ ， $\vec{b}$ 是单位向量，且 $\vec{a} \cdot \vec{b} = \frac{1}{2}$ ，则以下结论正确的是（）．

A、若 $\vec{a} = (1 ， 0)$ ，则 $\vec{b} = (\frac{1}{2} ， \frac{\sqrt{3}}{2})$ B、 $| \vec{a} + \vec{b} | = \sqrt{3}$ C、向量 $\vec{a}$ ， $\vec{b}$ 的夹角为 $\frac{2 π}{3}$ D、向量 $\vec{a}$ 在向量 $\vec{b}$ 上的投影向量为 $\frac{1}{2} \vec{b}$

查看试题解析
11. 已知函数 $f （ x ） = a s i n ω x + c o s ω x （ a$ 为常数， $ω > 0$ ）的图象有两条相邻的对称轴 $x = \frac{π}{6}$ 和 $x = - \frac{π}{3}$ ，则下列关于函数 $g （ x ） = s i n ω x + a c o s ω x$ 的说法正确的是（）

A、 $g （ x ）$ 的最大值为 $\sqrt{3} + 1$ B、 $g （ x ）$ 的图象关于直线 $x = \frac{π}{12}$ 对称 C、 $g （ x ）$ 在 $（ - \frac{π}{3} ， 0 ）$ 上单调递增 D、 $g （ x ）$ 的图象关于点 $（ \frac{π}{6} ， 0 ）$ 对称

查看试题解析
12. 2022年，为了加强疫情防控，某中学要求学生在校时每天都要进行体温检测．某班级体温检测员对一周内甲乙两名同学的体温进行了统计，其结果如图所示，则下列结论正确的是（）

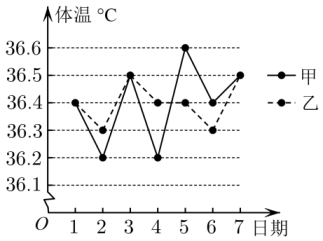A、乙同学体温的极差为 ${0.3}^{\circ} C$ B、甲同学体温的中位数与平均数相等 C、乙同学体温的方差比甲同学体温的方差小 D、甲同学体温的第60百分位数为 ${36.5}^{\circ} C$

查看试题解析

三、填空题（共4小题，每小题5分，共20分）

13. 用线性回归模型求得甲、乙、丙 $3$ 组不同的数据对应的 $R^{2}$ 的值分别为 $0.81 ， 0.98 ， 0.63$ ，其中（填甲、乙、丙中的一个）组数据的线性回归的效果最好.

查看试题解析
14. 数学兴趣小组对具有线性相关的两个变量x和y进行了统计分析，得到了下表：
x
4
6
8
10
12
y
a
2
b
c
6
并由表中数据求得y关于x的回归方程为 $\hat{y} = 0.65 x - 1.8$ ，若a ， b ， c成等差数列，则 $b =$ ．

查看试题解析
15. 已知随机变量 $ξ \sim N (1 ， σ^{2})$ ，且 $P (ξ \leq 0) = P (ξ \geq a)$ ，若 $x + y = a (x > 0 ， y > 0)$ ，则 $\frac{1}{x} + \frac{2}{y}$ 的最小值为．

查看试题解析
16. 十七世纪德国著名的天文学家开普勒曾经这样说过：“几何学里有两件宝，一个是勾股定理，另一个是黄金分割.如果把勾股定理比作黄金矿的话，那么可以把黄金分割比作钻石矿.”黄金三角形有两种，其中底与腰之比为黄金分割比的黄金三角形被认为是最美的三角形，它是一个顶角为 $36 °$ 的等腰三角形（另一种是顶角为108°的等腰三角形）.例如，五角星由五个黄金三角形与一个正五边形组成，如图所示，在其中一个黄金 $△ A B C$ 中， $\frac{B C}{A C} = \frac{\sqrt{5} - 1}{2}$ .根据这些信息，可得 $s i n 234 ° =$ .

查看试题解析

四、解答题（共6题，共70分）

17. 已知向量 $\overset{⃑}{a} = （ \sqrt{3} s i n x ， 1 ）$ ， $\overset{⃑}{b} = （ c o s x ， - 1 ）$ .

(1)、若 $\overset{⃑}{a}$ ∥ $\overset{⃑}{b}$ ，求 $t a n 2 x$ 的值；

(2)、若 $f （ x ） = （ \overset{⃑}{a} + \overset{⃑}{b} ） \cdot \overset{⃑}{b}$ ，求函数 $f （ x ）$ 的最小正周期及当 $x \in [0 ， \frac{π}{2}]$ 时的最大值.

查看试题解析
18. 在① $a = \sqrt{3} b s i n C + c c o s B$ ② ${s i n}^{2} A + {s i n}^{2} B - {s i n}^{2} C = 2 \sqrt{3} s i n A s i n B s i n C$ ③ $\overset{⃑}{A C} \cdot \overset{⃑}{A B} = b^{2} - \frac{\sqrt{3}}{2} a b$ 这三个条件中任选一个，补充在下面的横线上，并解答．
设 $△ A B C$ 的内角A ， B ， C ，所对的边分别为a ， b ， c ， ▲ ．

(1)、求角C；

(2)、若D是 $B C$ 上的点，且 $A D$ 平分 $∠ B A C$ ， $A D = 1$ ， $C D = \sqrt{2}$ ，求 $△ A B C$ 的面积．

查看试题解析
19. 某中学高三年级参加市数学联考，其中甲､乙两个班级优秀率分别为 $30 %$ 和 $40 %$ ，现在先从甲､乙两个班中选取一个班级，然后从选取的班级中再选出一名同学.选取甲､乙两个班级的规则如下：纸箱中有大小和质地完全相同的 $4$ 个白球､ $2$ 个黑球，从中摸出1个球，摸到白球就选甲班，摸到黑球就选乙班.

(1)、分别求出选取甲班､乙班的概率；

(2)、求选出的这名同学数学成绩优秀的概率.

查看试题解析
20. 已知正项数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，且 $a_{1} < 2$ ， $6 S_{n} = a_{n}^{2} + 3 a_{n} + 2$ .

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、若 $b_{n} = \frac{3}{a_{n} \cdot a_{n + 1}}$ ，求数列 ${b_{n}}$ 的前 $n$ 项和 $T_{n}$ .

查看试题解析
21. 2022年6月17日，我国第三艘航空母舰“中国人民解放军海军福建舰”下水试航，这是我国完全自主设计建造的首艘弹射型航空母舰，采用平直通长飞行甲板，配置电磁弹射和阻拦装置，满载排水量8万余吨．“福建舰”的建成，下水及试航，是新时代中国强军建设的重要成果．某校为纪念“福建舰”下水试航，增强学生的国防意识，组织了一次国防知识竞赛，共有100名学生参赛，成绩均在区间 $[50 ， 100]$ 上，现将成绩制成如图所示频率分布直方图（每组均包括左端点，最后一组包括右端点）．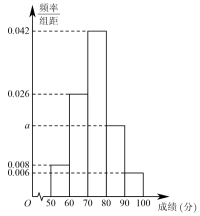
附： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ．

$P (K^{2} \geq k)$
0.050
0.010
0.001
k
3.841
6.635
10.828

(1)、学校计划对成绩不低于平均分的参赛学生进行奖励，若同一组中的数据用该组区间的中点值为代表，试求受奖励的分数线的估计值；

(2)、对这100名参赛学生的成绩按参赛者的性别统计，成绩不低于80分的为“良好”，低于80分的为“不良好”得到如下未填写完整的列联表．

良好
不良好
合计
男
48
女
16
合计
（ⅰ）将列联表填写完整；
（ⅱ）是否有95%以上的把握认为参赛学生的成绩是否良好与性别有关？

查看试题解析
22. $f (x) = x - a ln (1 + x)$ ，

(1)、讨论 $f (x)$ 的单调性；

(2)、当 $a = 1$ 时，证明 $f (x) \geq 0$ ；

(3)、证明对于任意正整数 $n$ ，都有 $\frac{1}{n} + \frac{1}{n + 1} + \frac{1}{n + 2} + \dots + \frac{1}{4 n - 1} + \frac{1}{4 n} > 2 ln 2$ .

查看试题解析

$P (K^{2} \geq k)$	0.050	0.010	0.001
k	3.841	6.635	10.828

	良好	不良好	合计
男			48
女	16
合计