河北省石家庄重点中学2023-2024学年高二上学期第三次调研数学试题

试卷更新日期：2023-12-27 类型：月考试卷

进入出卷网下载

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. 以椭圆 $\frac{x^{2}}{8} + \frac{y^{2}}{4} = 1$ 的长轴端点为焦点、以椭圆焦点为顶点的双曲线方程为（）

A、 $\frac{x^{2}}{4} - \frac{y^{2}}{4} = 1$ B、 $\frac{x^{2}}{8} - \frac{y^{2}}{4} = 1$ C、 $\frac{x^{2}}{4} - y^{2} = 1$ D、 $\frac{x^{2}}{8} - y^{2} = 1$

查看试题解析
2. 已知椭圆 $C ： \frac{x^{2}}{9} + \frac{y^{2}}{3} = 1$ 内一点 $M (1 ， 1)$ ，直线l与椭圆C交于A，B两点，且M为线段 $A B$ 的中点，则直线l的斜率为（）．

A、 $- 3$ B、 $- \frac{1}{3}$ C、3 D、 $\frac{1}{3}$

查看试题解析
3. 如图所示某拱桥的截面图可以看作双曲线 $\frac{y^{2}}{27} - \frac{x^{2}}{m} = 1$ 的图象的一部分，当拱顶M到水面的距离为 $\sqrt{3}$ 米时，水面宽 $A B$ 为 $2 \sqrt{7}$ 米，则此双曲线的虚轴长为（）

A、 $\sqrt{7}$ B、2 C、3 D、6

查看试题解析
4. 双曲线 $\frac{y^{2}}{a^{2}} - \frac{x^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的一条渐近线与y轴的夹角为 $30 °$ ，则该双曲线的离心率为（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\sqrt{3}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{2 \sqrt{3}}{3}$

查看试题解析
5. 已知 $A (0 ， 4)$ ，双曲线 $\frac{x^{2}}{4} - \frac{y^{2}}{5} = 1$ 的左、右焦点分别为 $F_{1} ， F_{2}$ ，点P是双曲线右支上一点，则 $△ P A F_{1}$ 周长的最小值为（）

A、10 B、12 C、14 D、16

查看试题解析
6. 已知椭圆 $\frac{x^{2}}{a_{1}^{2}} + \frac{y^{2}}{b_{1}^{2}} = 1 (a_{1} > b_{1} > 0)$ ，双曲线 $\frac{x^{2}}{a_{2}^{2}} - \frac{y^{2}}{b_{2}^{2}} = 1 (a_{2} > 0 ， b_{2} > 0)$ ，椭圆与双曲线有公共焦点 $F_{1} ， F_{2} ， P$ 是椭圆与双曲线的一个公共点，且 $∠ F_{1} P F_{2} = 60 °$ ，则下列说法正确的是（）

A、 $b_{1} = b_{2}$ B、 $b_{1} = \sqrt{3} b_{2}$ C、 $b_{1} = 2 b_{2}$ D、 $b_{1} = \sqrt{2} b_{2}$

查看试题解析
7. 唐代诗人李颀的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河．”在这首诗中含着一个有趣的数学问题——“将军饮马”问题．如图，在平面直角坐标系中，军营所在区域的边界为 $x^{2} + y^{2} = 1$ ，河岸所在直线方程为 $x + y = 3$ ，将军从点 $A (0 ， 2)$ 处出发，先到河边饮马，然后再返回军营，如果将军只要到达军营所在区域即回到军营，则这个将军所经过的最短路程为（）

A、 $\sqrt{5}$ B、 $\sqrt{5} - 1$ C、 $\sqrt{10}$ D、 $\sqrt{10} - 1$

查看试题解析
8. 已知A，B分别为椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右顶点，不同两点P，Q在椭圆C上，且关于x轴对称，设直线AP，BQ的斜率分别为m，n，则当 $\frac{a}{b} - \frac{1}{3 m n}$ 取最大值时，椭圆C的离心率为（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{2}}{3}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{5}}{3}$

查看试题解析

二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．

9. 已知平面直角坐标系中， $| A B | = 6$ ，点P为平面内一动点，且 $| P A | - | P B | = 2 a (a \in R)$ ，则下列说法正确的是（）

A、当 $a = 0$ 时，点P的轨迹为一条直线 B、当 $a = 3$ 时，点P的轨迹为一条射线 C、当 $a = - 3$ 时，点P的轨迹不存在 D、当 $a = 2$ 时，点P的轨迹是双曲线

查看试题解析
10. 已知直线l的方程为 $a x - y + 1 = 0 ， a \in R$ ，则下列说法正确的是（）

A、l与直线 $x + a y + 1 = 0$ 有唯一的交点 B、l与椭圆 $\frac{x^{2}}{2} + y^{2} = 1$ 一定有两个交点 C、l与圆 $(x - 1)^{2} + y^{2} = 4$ 一定有两个交点 D、满足与双曲线 $\frac{x^{2}}{2} - y^{2} = 1$ 有且只有一个公共点的直线l有2条

查看试题解析
11. 已知双曲线 $C ： x^{2} - y^{2} = 4$ 的左、右焦点分别为 $F_{1} ， F_{2}$ ，过双曲线C上的一点M作两条渐近线的垂线，垂足分别为 $P ， Q$ ，则（）

A、双曲线C的离心率为2 B、焦点到渐近线的距离为2 C、四边形 $O P M Q$ 可能为正方形 D、四边形 $O P M Q$ 的面积为定值2

查看试题解析
12. 已知曲线 $C ： x^{2} - 4 y | y | = 4 ， P (x_{0} ， y_{0})$ 为C上一点，则下列说法正确的是（）．

A、曲线C关于x轴对称 B、 $y_{0}$ 的取值范围为 $[- 1 ， + \infty)$ C、 $x_{0}^{2} + y_{0}^{2}$ 的取值范围为 $[1 ， + \infty)$ D、 $| x_{0} | > 2 y_{0}$

查看试题解析

三、填空题：本题共4小题，每小题5分，共20分．

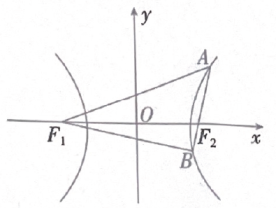
13. 已知方程 $\frac{x^{2}}{2 + m} - \frac{y^{2}}{m + 1} = 1$ 表示双曲线，求m的取值范围．

查看试题解析
14. 已知圆 $C_{1} ： x^{2} + y^{2} = r^{2}$ ，圆 $C_{2} ： x^{2} + y^{2} - 8 x - 6 y + 16 = 0$ ，若圆 $C_{1}$ 与圆 $C_{2}$ 相外切，则 $r =$ ．

查看试题解析
15. 双曲线 $\frac{x^{2}}{4} - \frac{y^{2}}{12} = 1$ 的左、右焦点分别是 $F_{1} ， F_{2} ， Q$ 是双曲线上的一点，且 $| Q F_{2} | = 5$ ，则 $| Q F_{1} | =$ ，过焦点 $F_{2}$ 作 $∠ F_{1} Q F_{2}$ 的角平分线的垂线，垂足为M，则 $| M O | =$ ．（第一空2分，第二空3分）

查看试题解析
16. 如图，双曲线 $E \cdot \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点分别为 $F_{1} ， F_{2} ， \vec{A F_{2}} = λ \vec{F_{2} B} (λ > 0)$ ，且 $c o s ∠ F_{1} A F_{2} = \frac{3}{5} ， B F_{1} ⊥ B F_{2}$ ，则双曲线E的离心率为．

查看试题解析

四、解答题：本题共6小题，共70分．解答应写出必要的文字说明、证明过程及演算步骤．

17. 分别求适合下列条件的双曲线的标准方程：

(1)、经过 $A (- 7 ， - 6 \sqrt{2}) ， B (2 \sqrt{7} ， 3)$ 两点；

(2)、与双曲线 $\frac{x^{2}}{2} - y^{2} = 1$ 有公共的渐近线，且过点 $(\sqrt{2} ， \sqrt{2})$ ．

查看试题解析
18. 动点 $M (x ， y)$ 与定点 $F (5 ， 0)$ 的距离和它到定直线 $l ： x = \frac{9}{5}$ 的距离的比是 $\frac{5}{3}$ ，记动点M的轨迹为曲线C．

(1)、求曲线C的方程；

(2)、若动点M在y轴右侧，定点 $A (5 ， 2)$ ，求 $| M A | + \frac{3}{5} | M F |$ 的最小值．

查看试题解析
19. 已知直线 $l ： y = k x - 1$ 与双曲线 $C ： x^{2} - y^{2} = 4$ 的两支各有一个交点，分别是 $P ， Q$ ．

(1)、求实数k的取值范围；

(2)、若 $△ P O Q$ 的面积为 $\sqrt{5}$ ，求实数k的值．

查看试题解析
20. 如图所示，半椭圆 $C_{1} ： \frac{x^{2}}{4} + \frac{y^{2}}{b^{2}} = 1 (0 < b < 2 ， y \leq 0)$ 和两个半圆 $C_{2} ： (x + 1)^{2} + y^{2} = 1 (y \geq 0) 、 C_{3} ： (x - 1)^{2} + y^{2} = 1 (y \geq 0)$ 组成了曲线 $C ： F (x ， y) = 0$ ，点 $F_{1} 、 F_{2}$ 依次为 $C_{1}$ 的左、右焦点．若点 $F_{1} ， F_{2}$ 分别为曲线 $C_{2} ， C_{3}$ 的圆心．

(1)、求曲线 $C_{1}$ 的方程；

(2)、直线l过点 $F_{2}$ 与半椭圆 $C_{1}$ 交于A，与半圆 $C_{3}$ 交于B，且 $\vec{A F_{2}} = 2 \vec{F_{2} B}$ ，求直线l的方程．

查看试题解析
21. 动点 $P (x ， y)$ 满足方程 $\sqrt{x^{2} + (y - 1)^{2}} + \sqrt{x^{2} + (y + 1)^{2}} = 4$ ．

(1)、求动点P的轨迹T的方程；

(2)、设过原点的直线l与轨迹T相交于 $A ， B$ 两点，设 $A (x_{1} ， y_{1}) ， F (0 ， 1)$ ，连接 $A F ， B F$ 并分别延长交轨迹T于点 $D ， E$ ，记 $△ A B F ， △ D E F$ 的面积分别是 $S_{1} ， S_{2}$ ，求 $\frac{S_{1}}{S_{2}}$ 的取值范围．

查看试题解析
22. 已知椭圆 $T ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的右顶点为A，上顶点为B，原点O到直线 $A B$ 的距离为 $\frac{\sqrt{3}}{2}$ ，且直线 $A B$ 的倾斜角 $\frac{5 π}{6}$ ．

(1)、求椭圆T的方程；

(2)、作直线 $A B$ 的平行线交椭圆于 $C ， D$ 两点，记直线 $A C ， B D$ 的斜率分别为 $k_{1} ， k_{2}$ ，求证： $k_{1} k_{2}$ 为定值．

查看试题解析