北师大版数学七年级上册期末冲刺满分攻略6 数轴
试卷更新日期:2023-12-27 类型:复习试卷
一、选择题
-
1. 有理数a、b、c、d在数轴上的对应点如图所示,这四个数中绝对值最小的是( )
 A、a B、b C、c D、d2. 若数轴上线段 , 点A表示的数是 , 则点B表示的数是( )A、2 B、 C、 D、或23. 如图,点A , B在数轴上对应的有理数分别为m , n , 若点A向右移动x个单位长度后到达B点,则x的值为( )
A、a B、b C、c D、d2. 若数轴上线段 , 点A表示的数是 , 则点B表示的数是( )A、2 B、 C、 D、或23. 如图,点A , B在数轴上对应的有理数分别为m , n , 若点A向右移动x个单位长度后到达B点,则x的值为( )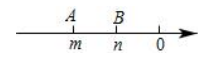 A、m B、 C、 D、n4. 已知a , b , c在数轴上对应的点如图所示,则代数式化简后的结果为( )
A、m B、 C、 D、n4. 已知a , b , c在数轴上对应的点如图所示,则代数式化简后的结果为( )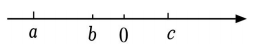 A、 B、 C、2b D、5. 下列说法正确的有( )
A、 B、 C、2b D、5. 下列说法正确的有( )相反数是它本身的数是;
绝对值是它本身的数是正数;
倒数是它本身的数是;
一个有理数不是整数就是分数;
数轴上距原点个单位的点表示的数是;
绝对值相等的两数互为相反数.
A、个 B、个 C、个 D、个6. 四位同学画数轴如下,其中正确的是( )A、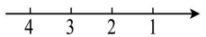 B、
B、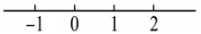 C、
C、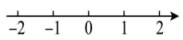 D、
D、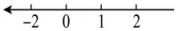 7. 如图所示,直径为单位1的圆从原点沿着数轴无滑动的逆时针滚动一周到达A点,则A点表示的数是( )
7. 如图所示,直径为单位1的圆从原点沿着数轴无滑动的逆时针滚动一周到达A点,则A点表示的数是( )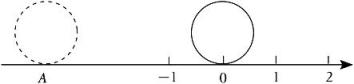 A、﹣2π B、﹣1+π C、﹣1+2π D、﹣π8. 已知a,b两数在数轴上对应的位置如图所示,则下列结论正确的是( )
A、﹣2π B、﹣1+π C、﹣1+2π D、﹣π8. 已知a,b两数在数轴上对应的位置如图所示,则下列结论正确的是( ) A、a+b>0 B、a-b>0 C、|a|>|b| D、ab<09. 如图,数轴上的点O和点A分别表示0和10,点P是线段OA上一动点.点P沿O→A→O以每秒2个单位的速度往返运动1次,B是线段OA的中点,设点P运动时间为t秒(t不超过10秒),若点P在运动过程中,当PB=2时,则运动时间t的值为( )
A、a+b>0 B、a-b>0 C、|a|>|b| D、ab<09. 如图,数轴上的点O和点A分别表示0和10,点P是线段OA上一动点.点P沿O→A→O以每秒2个单位的速度往返运动1次,B是线段OA的中点,设点P运动时间为t秒(t不超过10秒),若点P在运动过程中,当PB=2时,则运动时间t的值为( )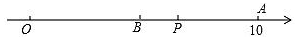 A、秒或秒 B、秒或秒或秒秒 C、3秒或7秒或或秒 D、秒或秒或秒秒10. 小明在写作业时不慎将一滴墨水滴在数轴上,根据如图的数值,判断墨迹盖住的整数共有个.( )
A、秒或秒 B、秒或秒或秒秒 C、3秒或7秒或或秒 D、秒或秒或秒秒10. 小明在写作业时不慎将一滴墨水滴在数轴上,根据如图的数值,判断墨迹盖住的整数共有个.( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 数轴上的点A与表示-3的点相距4个单位长度,则点A表示的数为12. 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第1次将点A向左移动3个单位长度到达点A1 , 第2次将点A1向右平移6个单位长度到达点A2 , 第3次将点A2向左移动9个单位长度到达点A3…则第6次移动到点A6;按照这种规律移动下去,至少移动次后该点到原点的距离不小于41.
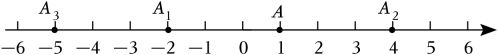 13. 已知数轴上有 , 两点, , 之间的距离为 , 点与原点的距离为 , 那么点对应的数是 .14. 数轴上有一动点 , 从原点出发沿着数轴移动,第一次点向左移动1个单位长度到达点 , 第二次将点向右移动2个单位长度到达点 , 第三次将点向左移动3个单位长度到达点 , 按照这种移动规律移动下去,第次移动到点 , 当时,点与原点的距离是个单位.15. 如图,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为24,OC边长为4,将长方形OABC沿数轴水平移动,移动后的长方形记为O'A'B'C',移动后的长方形O'A'B'C'与原长方形OABC重叠部分的面积为8,则点A'表示的数为 .
13. 已知数轴上有 , 两点, , 之间的距离为 , 点与原点的距离为 , 那么点对应的数是 .14. 数轴上有一动点 , 从原点出发沿着数轴移动,第一次点向左移动1个单位长度到达点 , 第二次将点向右移动2个单位长度到达点 , 第三次将点向左移动3个单位长度到达点 , 按照这种移动规律移动下去,第次移动到点 , 当时,点与原点的距离是个单位.15. 如图,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为24,OC边长为4,将长方形OABC沿数轴水平移动,移动后的长方形记为O'A'B'C',移动后的长方形O'A'B'C'与原长方形OABC重叠部分的面积为8,则点A'表示的数为 .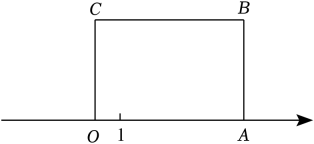 16. 在一条可以折叠的数轴上, , 表示的数分别是 , 4,如图,以点为折点,将此数轴向右对折,若点在点的右边,且 , 则点表示的数是 .
16. 在一条可以折叠的数轴上, , 表示的数分别是 , 4,如图,以点为折点,将此数轴向右对折,若点在点的右边,且 , 则点表示的数是 .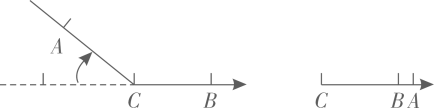
三、解答题
-
17. 有理数 , -4,2,0,
 (1)、在如图所示的数轴上表示以上各有理数;(2)、并用“<"号把它们按从小到大的顺序排列起来;(3)、若点B对应-4,点D对应2,请找出到点B、点D距离相等的点表示的数.18. 已知有理数 , b,c在数轴上的位置如图所示,
(1)、在如图所示的数轴上表示以上各有理数;(2)、并用“<"号把它们按从小到大的顺序排列起来;(3)、若点B对应-4,点D对应2,请找出到点B、点D距离相等的点表示的数.18. 已知有理数 , b,c在数轴上的位置如图所示, (1)、用<,>,=填空:+c0,c−b0,b+0,bc0;(2)、化简:|+c|+|c−b|−|b+|.(3)、已知2≤x≤6,求:|2-x|+|x-6|的值.19. 如图:在数轴上A点表示数a , B点表示数b , C点表示数c , 且a , c满足 , ,
(1)、用<,>,=填空:+c0,c−b0,b+0,bc0;(2)、化简:|+c|+|c−b|−|b+|.(3)、已知2≤x≤6,求:|2-x|+|x-6|的值.19. 如图:在数轴上A点表示数a , B点表示数b , C点表示数c , 且a , c满足 , , (1)、 , ;(2)、若将数轴折叠,使得A点与B点重合,则点C与数表示的点重合.(3)、在(1)(2)的条件下,若点P为数轴上一动点,其对应的数为x , 当代数式得最小值时,此时 , 最小值为;(4)、在(1)(2)的条件下,若在点B处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点C处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看做一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),请表示出甲、乙两小球之间的距离d(用t的代数式表示).20. 某市出租车的计价标准为:行驶路程不超过3千米收费10元,超过3千米的部分按每千米2.4元收费.(1)、若某人乘坐了x(x>3)千米,则他应支付车费元;(用含有x的代数式表示)(2)、一出租车公司坐落于东西方向的大道边,驾驶员王师傅从公司出发,在此大道上连续接送4批客人,行驶路程记录如下(规定向东为正,向西为负,单位:千米)
(1)、 , ;(2)、若将数轴折叠,使得A点与B点重合,则点C与数表示的点重合.(3)、在(1)(2)的条件下,若点P为数轴上一动点,其对应的数为x , 当代数式得最小值时,此时 , 最小值为;(4)、在(1)(2)的条件下,若在点B处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点C处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看做一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),请表示出甲、乙两小球之间的距离d(用t的代数式表示).20. 某市出租车的计价标准为:行驶路程不超过3千米收费10元,超过3千米的部分按每千米2.4元收费.(1)、若某人乘坐了x(x>3)千米,则他应支付车费元;(用含有x的代数式表示)(2)、一出租车公司坐落于东西方向的大道边,驾驶员王师傅从公司出发,在此大道上连续接送4批客人,行驶路程记录如下(规定向东为正,向西为负,单位:千米)第1批 第2批 第3批 第4批 +1.6 -9 +2.9 -7 ①送完第4批客人后,王师傅在公司的 边(填“东”或“西”),距离公司 千米的位置;
②在整个过程中,王师傅共收到车费多少钱?
③若王师傅的车平均每千米耗油0.1升,则送完第4批客人后,王师傅的车用了多少升油?
21. 如图,已知数轴上的点A表示的数为6,B是数轴上一点,且AB=10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒. (1)、写出点B表示的数 , 点P表示的数(用含t的代数式表示);(2)、动点R从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P、R同时出发,点P运动几秒时追上点R,并求出此时P表示的数;(3)、若M为AP的中点,N为PB的中点点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,请求出线段MN的长.22. 在数轴上,把原点记作点O,表示数1的点记作点A.对于数轴上任意一点P (不与点O,点A重合),记作 , 即= , 例如:当点P是线段OA的中点时,所以=1.
(1)、写出点B表示的数 , 点P表示的数(用含t的代数式表示);(2)、动点R从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P、R同时出发,点P运动几秒时追上点R,并求出此时P表示的数;(3)、若M为AP的中点,N为PB的中点点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,请求出线段MN的长.22. 在数轴上,把原点记作点O,表示数1的点记作点A.对于数轴上任意一点P (不与点O,点A重合),记作 , 即= , 例如:当点P是线段OA的中点时,所以=1. (1)、如图,点P1 , P2 , P3为数轴上三个点,点P1表示的数是 , 点P2与P1关于原点对称.
(1)、如图,点P1 , P2 , P3为数轴上三个点,点P1表示的数是 , 点P2与P1关于原点对称.①2=
②比较 , , 的大小(用“<”连接)
(2)、数轴上的点M满足OM=OA,求:(3)、数轴上的点P表示有理数p,已知<100且 , 则所有满足条件的p的倒数之和为23. 如图,半径为1的小圆与半径为2的大圆上有一点与数轴上原点重合,两圆在数轴上做无滑动的滚动,小圆的运动速度为每秒π个单位,大圆的运动速度为每秒2π个单位.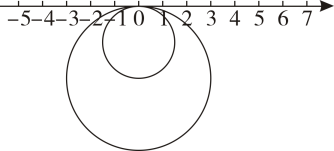 (1)、若大圆沿数轴向左滚动1周,则该圆与数轴重合的点所表示的数是;(2)、若小圆不动,大圆沿数轴来回滚动,规定大圆向右滚动时间记为正数,向左滚动时间记为负数,依次滚动的情况记录如下(单位:秒) :-1,+2,-4,-2,+3,-8
(1)、若大圆沿数轴向左滚动1周,则该圆与数轴重合的点所表示的数是;(2)、若小圆不动,大圆沿数轴来回滚动,规定大圆向右滚动时间记为正数,向左滚动时间记为负数,依次滚动的情况记录如下(单位:秒) :-1,+2,-4,-2,+3,-8①第次滚动后,大圆离原点最远?
②当大圆结束运动时,大圆运动的路程为?此时两圆与数轴重合的点之间的距离是?(结果保留π)
(3)、若两圆同时在数轴上各自沿着某一方向连续滚动,滚动一段时间后两圆与数轴重合的点之间相距9π,求此时两圆与数轴重合的点所表示的数.24. 如图,已知数轴上两点A、B.点C为数轴上的动点,其表示的数为x. (1)、若点C到点A、B的距离相等,则点C表示的数x的值为;(2)、式子|x-3|+|x+1|的最小值是;(3)、点D也是数轴上的一个动点,已知点C的运动速度为每秒2个单位长度,动点C、D同时分别从点A、B出发开始运动.
(1)、若点C到点A、B的距离相等,则点C表示的数x的值为;(2)、式子|x-3|+|x+1|的最小值是;(3)、点D也是数轴上的一个动点,已知点C的运动速度为每秒2个单位长度,动点C、D同时分别从点A、B出发开始运动.①若点C、D相向而行,在表示数的点相遇,求点D的运动速度;
②若点D的运动速度是每秒4个单位长度,C、D两点同时向左匀速运动,则当C、D两点之间的距离为2时,两点运动了多长时间?
(4)、若动点C从点A出发,第一次向左运动1个单位长度,第二次向右运动2个单位长度,第三次向左运动3个单位长度,…,按此规律不断在数轴上做往复运动,当点C运动了n次时,直接用含n的代数式表示出点C所表示的有理数.