2013年高考理数真题试卷（辽宁卷）

试卷更新日期：2016-09-28 类型：高考真卷

进入出卷网下载

一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 复数 $z = \frac{1}{i - 1}$ 的模长为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\sqrt{2}$ D、2

查看试题解析
2. 已知集合A={x|0＜log₄x＜1}，B={x|x≤2}，则A∩B=（）

A、（0，1） B、（0，2] C、（1，2） D、（1，2]

查看试题解析
3. 已知点A（1，3），B（4，﹣1），则与向量 $\vec{A B}$ 同方向的单位向量为（）

A、 $(\frac{3}{5}, - \frac{4}{5})$ B、 $(\frac{4}{5}, - \frac{3}{5})$ C、 $(- \frac{3}{5}, \frac{4}{5})$ D、 $(- \frac{4}{5}, \frac{3}{5})$

查看试题解析
4. 下列关于公差d＞0的等差数列{a_n}的四个命题：
p₁：数列{a_n}是递增数列；
p₂：数列{na_n}是递增数列；
p₃：数列 ${\frac{a_{n}}{n}}$ 是递增数列；
p₄：数列{a_n+3nd}是递增数列；
其中真命题是（）

A、p₁ ， p₂ B、p₃ ， p₄ C、p₂ ， p₃ D、p₁ ， p₄

查看试题解析
5. 某学校组织学生参加英语测试，成绩的频率分布直方图如图，数据的分组一次为[20，40），[40，60），[60，80），[80，100）．若低于60分的人数是15人，则该班的学生人数是（）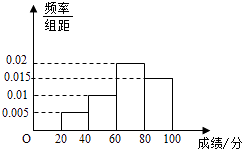

A、45 B、50 C、55 D、60

查看试题解析
6. 在△ABC，内角A，B，C所对的边长分别为a，b，c．asinBcosC+csinBcosA= $\frac{1}{2}$ b，且a＞b，则∠B=（）

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、 $\frac{2 π}{3}$ D、 $\frac{5 π}{6}$

查看试题解析
7. 使得（3x+ $\frac{1}{x \sqrt{x}}$ ）ⁿ（n∈N₊）的展开式中含有常数项的最小的n为（）

A、4 B、5 C、6 D、7

查看试题解析
8.
执行如图所示的程序框图，若输入n=10，则输出的S=（）

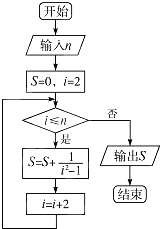A、 $\frac{5}{11}$ B、 $\frac{10}{11}$ C、 $\frac{36}{55}$ D、 $\frac{72}{55}$

查看试题解析
9. 已知点O（0，0），A（0，b），B（a，a³），若△OAB为直角三角形，则必有（）

A、b=a³ B、 $b = a^{3} + \frac{1}{a}$ C、 $(b - a^{3}) (b - a^{3} - \frac{1}{a}) = 0$ D、 $| b - a^{3} | + | b - a^{3} - \frac{1}{a} | = 0$

查看试题解析
10. 已知三棱柱ABC﹣A₁B₁C₁的6个顶点都在球O的球面上，若AB=3，AC=4，AB⊥AC，AA₁=12，则球O的半径为（）

A、 $\frac{3 + \sqrt{17}}{2}$ B、 $2 \sqrt{10}$ C、 $\frac{13}{2}$ D、 $3 \sqrt{10}$

查看试题解析
11. 已知函数f（x）=x²﹣2（a+2）x+a² ， g（x）=﹣x²+2（a﹣2）x﹣a²+8．设H₁（x）=max{f（x），g（x）}，H₂（x）=min{f（x），g（x）}，（max{p，q}）表示p，q中的较大值，min{p，q}表示p，q中的较小值），记H₁（x）的最小值为A，H₂（x）的最大值为B，则A﹣B=（）

A、16 B、﹣16 C、﹣16a²﹣2a﹣16 D、16a²+2a﹣16

查看试题解析
12. 设函数f（x）满足x²f′（x）+2xf（x）= $\frac{e^{x}}{x}$ ，f（2）= $\frac{e^{x}}{8}$ ，则x＞0时，f（x）（）

A、有极大值，无极小值 B、有极小值，无极大值 C、既有极大值又有极小值 D、既无极大值也无极小值

查看试题解析

二、填空题

13. 某几何体的三视图如图所示，则该几何体的体积是．

查看试题解析
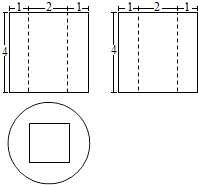14. 已知等比数列{a_n}是递增数列，S_n是{a_n}的前n项和．若a₁ ， a₃是方程x²﹣5x+4=0的两个根，则S₆= ．

查看试题解析
15. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 （ a > 0 ， b > 0 ）$ 的左焦点为F，C与过原点的直线相交于A，B两点，连接AF、BF，若|AB|=10，|AF|=6，cos∠ABF= $\frac{4}{5}$ ，则C的离心率e= ．

查看试题解析
16. 为了考察某校各班参加课外小组的人数，从全校随机抽取5个班级，把每个班级参加该小组的人数作为样本数据，已知样本平均数为7，样本方差为4，且样本数据互不相同，则样本数据中的最大值为．

查看试题解析

三、解答题：解答应写出文字说明、证明过程或演算步骤.

17. 设向量 $\vec{a} = (\sqrt{3} \sin x ， \sin x)$ ， $\vec{b} = (\cos x ， \sin x)$ ， $x \in [0 ， \frac{π}{2}]$ ．

(1)、若 $| \vec{a} | = | \vec{b} |$ ，求x的值；

(2)、设函数 $f (x) = \vec{a} \cdot \vec{b}$ ，求f（x）的最大值．

查看试题解析
18. 如图，AB是圆的直径，PA垂直圆所在的平面，C是圆上的点．

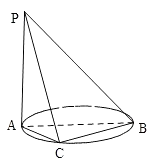(1)、求证：平面PAC⊥平面PBC；

(2)、若AB=2，AC=1，PA=1，求证：二面角C﹣PB﹣A的余弦值．

查看试题解析
19. 现有10道题，其中6道甲类题，4道乙类题，张同学从中任取3道题解答．

(1)、求张同学至少取到1道乙类题的概率；

(2)、已知所取的3道题中有2道甲类题，1道乙类题．设张同学答对甲类题的概率都是 $\frac{3}{5}$ ，答对每道乙类题的概率都是 $\frac{4}{5}$ ，且各题答对与否相互独立．用X表示张同学答对题的个数，求X的分布列和数学期望．

查看试题解析
20. 如图，抛物线C₁：x²=4y，C₂：x²=﹣2py（p＞0），点M（x₀ ， y₀）在抛物线C₂上，过M作C₁的切线，切点为A，B（M为原点O时，A，B重合于O），当x₀=1﹣ $\sqrt{2}$ 时，切线MA的斜率为﹣ $\frac{1}{2}$ ．

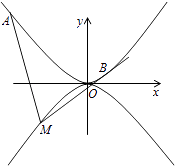(1)、求P的值；

(2)、当M在C₂上运动时，求线段AB中点N的轨迹方程（A，B重合于O时，中点为O）．

查看试题解析
21. 已知函数f（x）=（1+x）e^﹣^2x ， g（x）=ax+ $\frac{x^{3}}{2}$ +1+2xcosx，当x∈[0，1]时，

(1)、求证： $1 - x \leq f (x) \leq \frac{1}{1 + x}$ ；

(2)、若f（x）≥g（x）恒成立，求实数a的取值范围．

查看试题解析
22. 如图，AB为⊙O直径，直线CD与⊙O相切与E，AD垂直于CD于D，BC垂直于CD于C，EF垂直于F，连接AE，BE．证明：

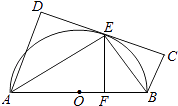(1)、∠FEB=∠CEB；

(2)、EF²=AD•BC．

查看试题解析
23. 在直角坐标系xOy中以O为极点，x轴正半轴为极轴建立坐标系．圆C₁ ，直线C₂的极坐标方程分别为ρ=4sinθ，ρcos（ $θ - \frac{π}{4}$ ）=2 $\sqrt{2}$ ．

(1)、求C₁与C₂交点的极坐标；

(2)、设P为C₁的圆心，Q为C₁与C₂交点连线的中点，已知直线PQ的参数方程为 ${\begin{matrix} x = t^{3} + a \\ y = \frac{b}{2} t^{3} + 1 \end{matrix}$ （t∈R为参数），求a，b的值．

查看试题解析
24. 已知函数f（x）=|x﹣a|，其中a＞1

(1)、当a=2时，求不等式f（x）≥4﹣|x﹣4|的解集；

(2)、已知关于x的不等式|f（2x+a）﹣2f（x）|≤2的解集{x|1≤x≤2}，求a的值．

查看试题解析