广西壮族自治区来宾市2023-2024学年九年级上学期期中数学试卷

试卷更新日期：2023-12-26 类型：期中考试

进入出卷网下载

一、单选题（12小题，每题3分，共36分）

1. 下列方程中，是一元二次方程的是（　　）

A、x²+ $\frac{1}{x}$ ＝0 B、x²+xy+1＝0 C、3x+2＝1 D、x²＝1

查看试题解析
2. 下列关系式中表示y是x的反比例函数的是（　　）

A、y＝ $\frac{x}{2}$ B、y＝2x+1 C、y＝ $\frac{1}{2}$ x² D、y＝ $\frac{2}{x}$

查看试题解析
3. 已知点（3，1）是反比例函数 $y = \frac{k}{x}$ 上一点，则下列各点中在该图象上的点是（　　）

A、（-1，3） B、 $(1 ， \frac{1}{3})$ C、 $(\frac{1}{3} ， - 9)$ D、 $(6 ， \frac{1}{2})$

查看试题解析
4. 若 $\frac{a}{b} = \frac{c}{d} = \frac{e}{f} = \frac{2}{3}$ ，则 $\frac{2 a + 5 c - 6 e}{2 b + 5 d - 6 f}$ 的值为（　　）

A、 $\frac{3}{2}$ B、 $\frac{2}{3}$ C、 $\frac{2}{5}$ D、 $\frac{5}{6}$

查看试题解析
5. 关于反比例函数y＝ $\frac{3}{x}$ 的图象性质，下列说法正确的是（　　）

A、图象位于第二、四象限 B、图象经过点（1，3） C、当x＞0时，y随x的增大而增大 D、y随x的增大而减小

查看试题解析
6. 如图所示，过反比例函数y＝ $\frac{k}{x}$ （k＞0）在第一象限内的图象上任意两点A ， B ，分别作x轴的垂线，垂足分别为C ， D ，连接OA ， OB，设△AOC与△BOD的面积为S₁ ， S₂ ，那么它们的大小关系是（　　）

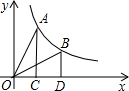A、S₁＞S₂ B、S₁＝S₂ C、S₁＜S₂ D、不能确定

查看试题解析
7. 如果关于x的一元二次方程kx²-6x+9＝0有两个不相等的实数根，那么k的取值范围是（　　）

A、k＜1 B、k≠0 C、k＜1且k≠0 D、k＞1

查看试题解析
8. 把一元二次方程x²+12x+27＝0化为（x+p）²＝q的形式，正确的是（　　）

A、（x-6）²＝9 B、（x+6）²＝9 C、（x+12）²＝-27 D、（x+6）²＝-27

查看试题解析
9. 如图，这是一个简单的数值运算程序，则输入x的值为（　　）

A、x₁＝2，x₂＝-2 B、x₁＝3，x₂＝-3 C、x₁＝3，x₂＝-1 D、x₁＝-3，x₂＝1

查看试题解析
10. 如图，是某商店售卖的花架简图，其中AD∥BE∥CF，DE=24cm，EF=40cm，BC=50cm，则AB长为（　　）cm.

A、 $\frac{80}{3}$ B、 $\frac{100}{3}$ C、50 D、30

查看试题解析
11. 反比例函数y＝ $\frac{m - 1}{x}$ （m≠1）与y＝ $\frac{m + 1}{x}$ （m≠-1）的图象交点情况为（　　）

A、没有交点 B、有且只有一个交点 C、有两个交点 D、有无数个交点

查看试题解析
12. 如图，正方形MNPQ的顶点P ， Q分别在反比例函数 $y = \frac{k_{1}}{x}$ ， $y = \frac{k_{2}}{x}$ 的图象上，点M，N在x轴上，PQ交y轴于点G，连接NQ交y轴于点H，若HO=2GH，则 $\frac{k_{1}}{k_{2}}$ ＝（　　）

A、 $- \frac{1}{2}$ B、-2 C、 $\frac{1}{2}$ D、2

查看试题解析

二、填空题（6小题，每题2分，共12分）

13. 方程x（x﹣2）=0的解为．

查看试题解析
14. 如图，在 $△ A B C$ 中，D、E分别是AB、AC的中点，则 $\frac{A D}{A B} =$ ．

查看试题解析
15. 某新能源汽车每小时充电3kW•h，充满电量需要7h，1kW•h的电量可行驶8km，则充满电后平均每天行驶的里程数s（km）与可行驶天数n（天）之间的关系式为．

查看试题解析
16. 如图，四边形ABCD∽四边形A'B'C'D'，若∠B=60°，∠C=80°，∠A'=100°，则∠D= ．

查看试题解析
17. 在平面直角坐标系中，反比例函数 $y = \frac{k}{x}$ 的部分图象如图所示， AB⊥y轴于点B，点P在x轴上，若△ABP的面积为2，则k的值为．

查看试题解析
18. 若a ， b是方程x²-2x-5＝0的两个实数根，则（a-2）（b-2）的值为．

查看试题解析

三、解答题（共8小题，共72分）

19. 解方程：（x+1）²-9＝0．

查看试题解析
20. 解方程：x²﹣4x﹣5＝0.

查看试题解析
21. 某种病毒传播非常快，如果一个人被感染，经过两轮感染后就会有121个人被感染.

(1)、每轮感染中平均一个人会感染几个人？

(2)、若病毒得不到有效控制，3轮感染后，被感染的人会不会超过1300人？

查看试题解析
22. 如图，直线y＝k₁x+b与反比例函数y＝ $\frac{k_{2}}{x}$ 的图象相交于点A、B ，与x轴交于点C ，其中点A的坐标为（-2，4），点B的横坐标为-4．

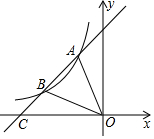(1)、试确定反比例函数的表达式；

(2)、求C的坐标．

查看试题解析
23. 阅读材料：为解方程（x²-1）²-5（x²-1）+4＝0，我们可以将x²-1看作一个整体，设x²-1＝y ，则原方程可化为
y²-5y+4＝0①，解得y₁＝1，y₂＝4．
当y＝1时，x²-1＝1，∴x²＝2，∴x＝± $\sqrt{2}$ ．
当y＝4时，x²-1＝4，x²＝5，∴x＝± $\sqrt{5}$ ．
故原方程的解为x₁＝ $\sqrt{2}$ ， x₂＝- $\sqrt{2}$ ， x₃＝ $\sqrt{5}$ ， x₄＝- $\sqrt{5}$ ．
解答问题：

(1)、上述解题过程，在由原方程得到方程①的过程中，利用法达到了降次的目的．

(2)、请利用以上知识解方程（x²+x）²-4（x²+x）+3＝0．

查看试题解析
24. 如图1，某校准备一面利用墙，其余三面用篱笆围成一个矩形花圃ABCD，已知旧墙可利用的最大长度为13m，篱笆长为24m.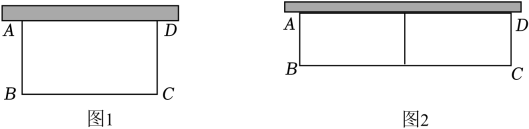

(1)、若围成的花圃面积为70m² ，求BC的长．

(2)、如图2，若计划将花圃中间用一道篱笆隔成两个小矩形，且花圃面积为78m² ，请你判断能否围成这样的花圃．如果能，求BC的长；如果不能，请说明理由．

查看试题解析
25. 向阳中学有一块正方形的空地，边长为40m，学校计划将空地分为五部分，种植不同的花束．白老师利用课后延时时间将设计任务交给小明和小芳两位同学，并给两位同学每人一张边长为20cm的正方形硬纸板模型用来设计，下面是小明和小芳的设计方案．
小明：如图1，它是由四个矩形和中间一个小正方形组成的，在该图案中矩形①与矩形②为相似矩形，相似比为1：3，中间小正方形的边长为4cm.
小芳：如图2，它是由四个全等的直角三角形以及一个小正方形组成的，其中小正方形与大正方形的相似比为1：5．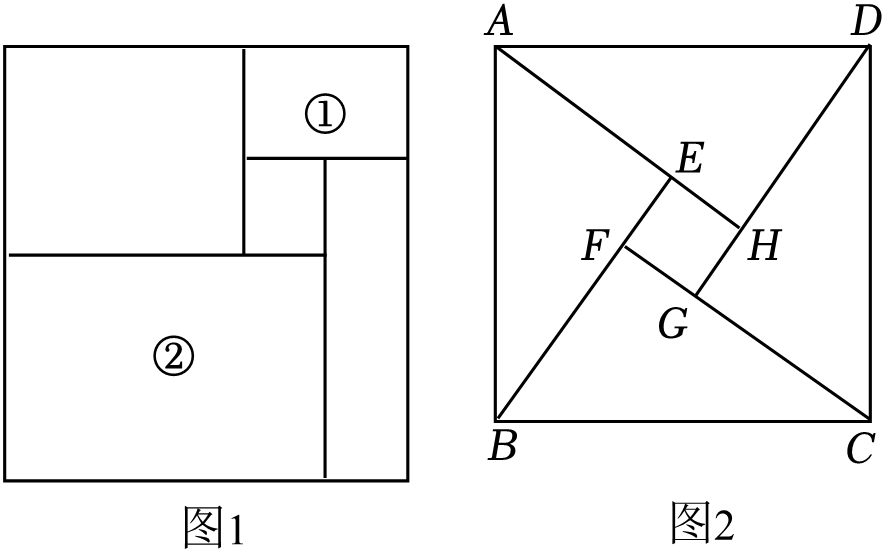

(1)、求小明的方案中矩形①的面积．

(2)、求小芳设计的方案中，每个小直角三角形部分在学校空地的实际周长是多少米？

查看试题解析
26. 如图，一次函数y=kx+b的图象经过第一、二、三象限，且与反比例函数图象相交于A，B两点，与x轴交于点D，OB= $\sqrt{5}$ ，且点B的横坐标是点B的纵坐标的2倍．

(1)、求反比例函数的解析式．

(2)、如图，一次函数y=kx+b的图象向下平移10个单位长度，得到新的函数图象与x轴交于点C．设点A的横坐标为m，若△ABC的面积S=15，求m的值．

查看试题解析