陕西省西安市蓝田县2023-2024学年八年级上学期数学期中试卷

试卷更新日期：2023-12-26 类型：期中考试

进入出卷网下载

一、选择题（共8小题，每小题3分，计24分。）

1. 下列四个数中，是无理数的是（）

A、 $\frac{23}{7}$ B、0 C、0.12 D、 $π$

查看试题解析
2. 点 $(- 2 ， 3)$ 在平面直角坐标系中所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 以下四组数中，是勾股数的是（）

A、1，2，3 B、12，13，4 C、8，15，17 D、4，5，6

查看试题解析
4. 下列各式中，计算正确的是（）

A、 $\sqrt{2} + \sqrt{5} = \sqrt{7}$ B、 $2 \sqrt{3} - \sqrt{3} = 2$ C、 $\sqrt{3^{2} - 2^{2}} = 1$ D、 $2 \sqrt{5} \times \sqrt{5} = 10$

查看试题解析
5. 函数 $y = 2 x^{m - 1}$ 是关于 $x$ 的正比例函数，则 $m$ 的值是（）

A、3 B、2 C、1 D、0

查看试题解析
6. 在平面直角坐标系中，点 $A$ 与点 $B$ 关于 $y$ 轴对称，若点 $A$ 的坐标为 $(3 ， 4)$ ，则线段 $A B$ 的长度为（）

A、4 B、3 C、6 D、8

查看试题解析
7. 若 $a < - 1$ ，则一次函数 $y = (a + 1) x + 1 - a$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
8. 如图，钓鱼竿 $A B$ 的长为6m，露在水面上的鱼线 $B C$ 长为2m．钓鱼者想看鱼上钩的情况，把钓鱼竿 $A B$ 调整到 $A B^{'} (A B^{'} = A B)$ 的位置，此时露在水面上的鱼线 $B^{'} C^{'}$ 长为 $3 \sqrt{2} m$ ，则 $C C^{'}$ 的长为（）

A、 $\sqrt{2} m$ B、 $2 \sqrt{2} m$ C、 $\sqrt{3} m$ D、 $2 \sqrt{3} m$

查看试题解析

二、填空题（共5小题，每小题3分，计15分）

9. -27的立方根是.

查看试题解析
10. 将函数 $y = 2 x + 3$ 的图象向下平移2个单位长度后，得到的新图象的函数表达式为。

查看试题解析
11. 实数 $a$ 、 $b$ 在数轴上的位置如图所示，若无理数 $c$ 满足 $b < c < a$ ，则 $c$ 的值可以是。（填一个即可）

查看试题解析
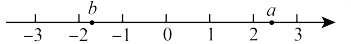12. 已知一次函数 $y = k x + b$ （ $k$ ， $b$ 为常数，且 $k \neq 0)$ 的图象经过第一、二、四象限，若点 $A (1 ， a)$ ， $B (- 1 ， b)$ 在该函数的图象上，则 $a$ b。（填“>”“<”或“=”）

查看试题解析
13. 如图，是一个三级台阶，它的每一级的长、宽，高分别为 $20 d m$ ， $3 d m$ 、 $2 d m$ ， $A$ 和 $B$ 是这个台阶两个相对的端点， $A$ 点有一只蚂蚁，想到 $B$ 点去吃可口的食物，则蚂蚁沿着台阶面爬到 $B$ 点的最短路程是 $d m$ 。

查看试题解析

三、解答题（共13小题，计81分．解答应写出过程）

14. 计算： $4 \sqrt{5} - \sqrt{3} \times \sqrt{15} + \sqrt{18} \div \sqrt{2}$ 。

查看试题解析
15. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 3 + \sqrt{5}$ ， $B C = 3 - \sqrt{5}$ ，求 $A B$ 的长。

查看试题解析
16. 已知最简二次根式 $\sqrt{a - 2}$ 与 $\sqrt{24}$ 可以合并，求 $a$ 的值。

查看试题解析
17. 已知点 $P (2 m + 4 ， m - 1)$ ，试分别根据下列条件，求出点 $P$ 的坐标。

(1)、点 $P$ 在 $y$ 轴上；

(2)、点 $P$ 在第四象限，且到 $x$ 轴的距离为2。

查看试题解析
18. 已知正比例函数的图象经过点 $(- 3 ， 6)$ 。

(1)、求这个正比例函数关系式；

(2)、若这个图象还经过点 $A (a ， 8)$ ，求点 $A$ 的坐标。

查看试题解析
19. 已知一个正数的两个平方根分别是 $2 a + 1$ 和 $a - 4$ ，又 $b - 4$ 的立方根为-2。

(1)、求 $a$ ， $b$ 的值；

(2)、求 $5 a - b$ 的算术平方根。

查看试题解析
20. 周末，小聪和爸爸、妈妈到动物园游玩，回家后，他利用所学的平面直角坐标系画出了动物园的景区示意图，如图所示，可是他忘记了在图中标出原点和 $x$ 轴、 $y$ 轴，却知道马场的坐标为 $(- 1 ， - 1)$ ，狮子园的坐标为 $(- 2 ， 2)$ ，请你帮他建立平面直角坐标系并写出其他景点的坐标。（点 $A$ 为马场，点 $B$ 为南门，点 $C$ 为两栖动物园，点 $D$ 为飞禽园，点 $E$ 为狮子园）

查看试题解析
21. 如图，在 $△ A B C$ 中，点 $D$ 在边 $B C$ 上，连接 $A D$ ，过点 $D$ 作 $D E ⊥ A C$ 于点 $E$ ， $C E = 2$ ， $D E = 4$ ， $A E = 8$ ．试说明 $∠ A D C = 90 °$ 。

查看试题解析
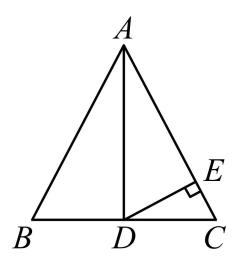22. 如图，在平面直角坐标系中， $△ A B C$ 的三个顶点坐标分别为 $A (- 2 ， 4)$ 、 $B (4 ， 2)$ ， $C (2 ， 1)$ 。

(1)、作 $△ A B C$ 关于 $x$ 轴的对称图形 $△ A_{1} B_{1} C_{1}$ ，点 $A$ ， $B$ ， $C$ 的对应点分别为 $A_{1}$ ， $B_{1}$ ， $C_{1}$ ；

(2)、在（1）的条件下，写出点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的坐标。

查看试题解析
23. 请根据如图所示的对话内容回答下列问题．

(1)、求该魔方的棱长；

(2)、求该长方体纸盒的长．

查看试题解析
24. 联通公司手机话费收费有 $A$ 套餐（月租费15元，通话费每分钟0.1元）和 $B$ 套餐（月租费0元，通话费每分钟0.15元）两种，设 $A$ 套餐每月话费为 $y_{1}$ （元）， $B$ 套餐每月话费为 $y_{2}$ （元），月通话时间为 $x$ 分钟。

(1)、分别表示出 $y_{1}$ 与 $x$ ， $y_{2}$ 与 $x$ 的函数关系式；

(2)、如果该手机用户使用 $A$ 套餐且本月缴费50元，求他本月的通话时间?

(3)、若该用户这个月的通话时间为160分钟，请分别计算使用套餐 $A$ 和套餐 $B$ 应缴费多少元?

查看试题解析
25. 台风是一种自然灾害，它以台风中心为圆心在周围上千米的范围内形成极端气候，有极强的破坏力。如图，有一台风中心沿东西方向 $A B$ 由点 $A$ 向点 $B$ 移动，已知点 $C$ 为一海港，且点 $C$ 与直线 $A B$ 上两点 $A$ ， $B$ 的距离 $C A$ 、 $C B$ 分别为 $300 k m$ 、 $400 k m$ ，又 $A B = 500 k m$ ，以台风中心为圆心周围 $250 k m$ 以内为受影响区域。

(1)、海港 $C$ 受台风影响吗?为什么?

(2)、若台风中心移动的速度为 $20 k m / h$ ，台风影响海港 $C$ 持续的时间有多长?

查看试题解析
26. 如图，在平面直角坐标系中，一次函数 $y = - x + n$ 的图象与正比例函数 $y = 2 x$ 的图象交于点 $A (m ， 4)$ ，设一次函数 $y = - x + n$ 的图象与 $x$ 轴交于点 $B$ ，与 $y$ 轴交于点 $C$ 。

(1)、求 $m$ ， $n$ 的值；

(2)、求点 $B$ ，点 $C$ 的坐标；

(3)、在 $x$ 轴上是否存在点 $P$ 使 $△ P A B$ 为等腰三角形，若存在，请求出点 $P$ 的坐标；若不存在，请说明理由。

查看试题解析