重庆市沙坪坝区第八名校2023-2024学年高一上学期数学12月月考试卷
试卷更新日期:2023-12-26 类型:月考试卷
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 已知集合 , 则( )A、 B、 C、 D、2. “”是“”的( )A、充要条件 B、必要不充分条件 C、充分不必要条件 D、既不充分也不必要条件3. 函数的零点所在区间为( )A、 B、 C、 D、4. 若 , 幂函数在上单调递减,则实数的值为( )A、 B、3 C、或3 D、5. 已知函数 , 则的定义域为( )A、 B、 C、 D、6. 小明使用一架两臂不等长的天平称黄金.小明先将的砝码放在天平左盘中,取出一些黄金放在天平右盘中使天平平衡;再将的砝码放在天平右盘中,再取出一些黄金放在天平左盘中使天平平衡,你认为小明两次称得的黄金总重量( )(附:依据力矩平衡原理,天平平衡时有 , 其中分别为左右盘中物体质量,分别为左右横梁臂长).A、等于 B、小于 C、大于 D、与左右臂的长度有关7. 若函数在上有意义且不单调,则的取值范围是( )A、 B、 C、 D、8. 若函数是偶函数,则的取值范围是( )A、 B、 C、 D、
二、多选题:本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
-
9. 下列大小关系正确的是( )A、 B、 C、 D、10. 若“”为假命题,则的值可能为( )A、 B、0 C、2 D、411. 函数的大致图象可能是( )A、
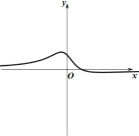 B、
B、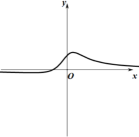 C、
C、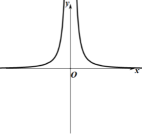 D、
D、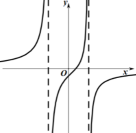 12. 已知函数 , 则下列选项正确的是( )A、函数的值域为 B、方程有两个不等的实数解 C、不等式的解集为 D、关于的方程的解的个数可能为
12. 已知函数 , 则下列选项正确的是( )A、函数的值域为 B、方程有两个不等的实数解 C、不等式的解集为 D、关于的方程的解的个数可能为三、填空题:本大题共4小题,每小题5分,共20分.
-
13. 已知函数在上有一个零点,用二分法求零点的近似值(精确度为0.1时,至少需要进行次函数值的计算.14. 已知 , 则 .15. 若函数在上只有一个零点,则实数的取值范围是.16. 已知函数 , 若 , 则实数的取值范围为.
四、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.
-
17. 已知集合 , 集合.(1)、若 , 求;(2)、若 , 求实数的取值范围.18. 已知函数.(1)、若的解集为 , 求实数的值;(2)、若 , 求不等式的解集.19. 塑料袋给我们生活带来了方便,但对环境造成了巨大危害.某品牌塑料袋经自然降解后残留量与时间年之间的关系为为初始量,为光解系数(与光照强度、湿度及氧气浓度有关),为塑料分子聚态结构系数.(参考数据:)(1)、已知塑料分子聚态结构系数是光解系数的90倍,若塑料自然降解到残留量为初始量的时,大约需要多少年?(2)、为了缩短降解时间,该品牌改变了塑料分子聚态结构,其他条件不变.已知2年就可降解初始量的.要使残留量不超过初始量的5%,至少需要多少年?20. 已知函数 , 函数.(1)、求函数的解析式;(2)、若图象恒在图象的下方,求实数的取值范围.