广东省中山市小榄镇2023-2024学年八年级上学期数学期中试卷
试卷更新日期:2023-12-26 类型:期中考试
一、选择题(每小题3分,共30分)
-
1. 下列每组数分别表示3根小木棒的长度(单位: , 其中能搭成一个三角形的是( )A、5,7,12 B、7,7,15 C、6,9,16 D、6,8,122. 在下列图形中,( )一定是轴对称图形.A、平行四边形 B、梯形 C、圆 D、三角形3. 在中, , , 则的度数是( )A、 B、 C、 D、4. 已知等腰三角形的两条边长分别为2和5,则它的周长为( )
A、9 B、12 C、9或12 D、55. 在平面直角坐标系中,点关于轴对称的点的坐标是( )A、 B、 C、 D、6. 如图,已知 , 那么添加下列一个条件后,仍无法判定的是( ) A、 B、 C、 D、7. 如图, , , 分别是的中线、角平分线、高线,下列结论中错误的是( )
A、 B、 C、 D、7. 如图, , , 分别是的中线、角平分线、高线,下列结论中错误的是( ) A、 B、 C、 D、8. 如图,中, , 沿折叠 , 使点恰好落在边上的点处,若 , 则等于( )
A、 B、 C、 D、8. 如图,中, , 沿折叠 , 使点恰好落在边上的点处,若 , 则等于( ) A、 B、 C、 D、9. 如图,中, , , , 点是边上的动点,则长不可能是( )
A、 B、 C、 D、9. 如图,中, , , , 点是边上的动点,则长不可能是( ) A、3.5 B、4.2 C、5.8 D、7.310. 如图,已知是的平分线, , 若 , 则△ABC的面积等于( )
A、3.5 B、4.2 C、5.8 D、7.310. 如图,已知是的平分线, , 若 , 则△ABC的面积等于( ) A、 B、 C、 D、不能确定
A、 B、 C、 D、不能确定二、填空题(每小题3分,共18分)
-
11. 如图,与△关于直线对称,则的度数为 .
 12. 如图,工人师傅在安装木制门框时,为防止变形,常常钉上两条斜拉的木条,这样做的数学依据是.
12. 如图,工人师傅在安装木制门框时,为防止变形,常常钉上两条斜拉的木条,这样做的数学依据是. 13. 已知三角形的三边长分别是8、10、x,则x的取值范围是.14. 如图,在△ABC中,AB的垂直平分线分别交BC,AB于D,E两点,若 , △ADC的周长为9cm,则△ABC的周长是.
13. 已知三角形的三边长分别是8、10、x,则x的取值范围是.14. 如图,在△ABC中,AB的垂直平分线分别交BC,AB于D,E两点,若 , △ADC的周长为9cm,则△ABC的周长是. 15. 如图,是一个3×3的正方形网格,则∠1+∠2+∠3+∠4=。
15. 如图,是一个3×3的正方形网格,则∠1+∠2+∠3+∠4=。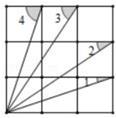 16. 如图,在中, , , , , 是的平分线.若 , 分别是和上的动点,则的最小值是 .
16. 如图,在中, , , , , 是的平分线.若 , 分别是和上的动点,则的最小值是 .
三、解答题(每小题6分,共24分)
-
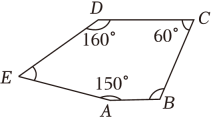
17. 一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数.18. 已知如图,五边形中, , 求图中的值.
 19. 如图,已知 , , 求证: .
19. 如图,已知 , , 求证: . 20. 如图,已知 , 利用尺规作图法求作边的中线 . (不写作法,保留作图痕迹)
20. 如图,已知 , 利用尺规作图法求作边的中线 . (不写作法,保留作图痕迹)
四、解答题(每小题7分,共21分)
-
21. 如图,在平面直角坐标系中, , , .
 (1)、点关于轴的对称点的坐标为;(2)、请画出关于轴对称的图形△;(3)、将向右平移2个单位,向下平移1个单位,得到△ , 请直接写出△的顶点坐标.22. 如图,在中,点为边上一点,连结并延长到点 , 过点作交于点 , 交于点 .
(1)、点关于轴的对称点的坐标为;(2)、请画出关于轴对称的图形△;(3)、将向右平移2个单位,向下平移1个单位,得到△ , 请直接写出△的顶点坐标.22. 如图,在中,点为边上一点,连结并延长到点 , 过点作交于点 , 交于点 . (1)、若 , 求证:;(2)、若 , , , 求的度数.23. 如图,是等边三角形,是中线,延长至 , 使 , , 垂足为点 .
(1)、若 , 求证:;(2)、若 , , , 求的度数.23. 如图,是等边三角形,是中线,延长至 , 使 , , 垂足为点 . (1)、求证:;(2)、若 , 求的周长.
(1)、求证:;(2)、若 , 求的周长.五、解答题(每小题9分,共27分)


