黑龙江省哈尔滨市阿城区2023-2024学年九年级上学期数学期中试卷

试卷更新日期：2023-12-26 类型：期中考试

进入出卷网下载

一、选择题（每小题3分，共计30分）

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 方程 $x^{2} = 3 x$ 的解是（ $)$

A、 $x = 3$ B、 $x_{1} = 0$ ， $x_{2} = 3$ C、 $x_{1} = 0$ ， $x_{2} = - 3$ D、 $x_{1} = 1$ ， $x_{2} = 3$

查看试题解析
3. 已知函数y= $(m - 3) x^{m^{2} - 7}$ 是二次函数，则m的值为（）

A、-3 B、±3 C、3 D、± $\sqrt{7}$

查看试题解析
4. 已知⊙O的半径是5，OP的长为7，则点P与⊙O的位置关系是（）

A、点P在圆内 B、点P在圆上 C、点P在圆外 D、不能确定

查看试题解析
5. 在平面直角坐标系中，如果抛物线 $y = 2 x^{2}$ 不动，而把x轴、y轴分别向上、向右平移2个单位，那么在新坐标系下抛物线的解析式是（）

A、 $y = 2 {(x - 2)}^{2} + 2$ B、 $y = 2 {(x - 2)}^{2} - 2$ C、 $y = 2 {(x + 2)}^{2} - 2$ D、 $y = 2 {(x + 2)}^{2} + 2$

查看试题解析
6.
如图，A、B、C在⊙O上，∠OAB=22.5°，则∠ACB的度数是（　　）

A、11.5° B、112.5° C、122.5° D、135°

查看试题解析
7. 设 $A (- 2 ， y_{1})$ ， $B (1 ， y_{2})$ ， $C (2 ， y_{3})$ 是抛物线 $y = - {(x + 1)}^{2} + 2$ 上的三点，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系为（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{1} > y_{3} > y_{2}$ C、 $y_{3} > y_{2} > y_{1}$ D、 $y_{3} > y_{1} > y_{2}$

查看试题解析
8. 如图，以 $O$ 为圆心的两个同心圆中，大圆的弦 $A B$ 是小圆的切线，点 $P$ 为切点.若大圆半径为2，小圆半径为1，则 $A B$ 的长为（）

A、 $\sqrt{3}$ B、 $2 \sqrt{3}$ C、 $\sqrt{5}$ D、2

查看试题解析
9. ⊙O的半径为5cm，弦AB//CD ，且AB=8cm，CD=6cm，则AB与CD之间的距离为( )

A、1 cm B、7cm C、3 cm或4 cm D、1cm 或7cm

查看试题解析
10. 如图，二次函数 $y = a x^{2} + b x + c$ （ $a \neq 0$ ）的图象与 $x$ 轴交于点 $A$ 、 $B$ 两点，与 $y$ 轴交于点 $C$ ，对称轴为直线 $x = - 1$ ，点 $B$ 的坐标为 $(1 ， 0)$ ，则下列结论：① $A B = 4$ ；② $b^{2} - 4 a c > 0$ ；③ $a b < 0$ ；④ $a^{2} - a b + a c < 0$ ，其中正确的结论有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析

二、填空题（每小题3分，共24分）

11. 已知关于x的方程x²+3x+k²＝0的一个根是﹣1，则k＝.

查看试题解析
12. 在直角坐标系中，点 $A (1 ， - 2)$ 关于原点对称的点的坐标是．

查看试题解析
13. 如图，P是 $⊙ O$ 的直径 $B A$ 延长线上一点，点D在 $⊙ O$ 上， $P D$ 交 $⊙ O$ 于点C ，且 $P C = O D$ ，如果 $∠ P = 24 °$ ，则 $∠ D O B =$ ．

查看试题解析
14. 如果二次函数y＝x²﹣8x+m﹣1的顶点在x轴上，那么m＝.

查看试题解析
15. 如图，已知一块圆心角为270°的扇形铁皮，用它做一个圆锥形的烟囱帽（接缝忽略不计），圆锥底面圆的直径是60cm，则这块扇形铁皮的半径是cm.

查看试题解析
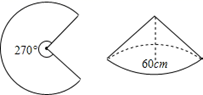16. 一种药品原价每盒25元，两次降价后每盒16元.设两次降价的百分率都为x，可列方程.

查看试题解析
17. 如图，已知 $⊙ P$ 的半径为2，圆心P在抛物线 $y = \frac{1}{2} x^{2} - 2$ 上运动；当 $⊙ P$ 与x轴相切时；圆心P的坐标为.

查看试题解析
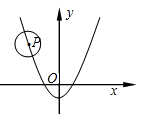18. 如图，已知直线 $y = \frac{3}{4} x - 3$ 与x轴、y轴分别交于A、B两点，点P是以 $C (0 ， 1)$ 为圆心，1为半径的圆上一动点，连接 $P A ， P B$ ．则 $△ P A B$ 面积的最大值与最小值的差为．

查看试题解析

三、解答题（19~24题每题6分，25~27题每题10分，共66分）

19. 解方程：

(1)、 $x^{2} - 8 x - 9 = 0$ ；

(2)、 $x^{2} - x - 1 = 0$ ．

查看试题解析
20. 如图， $△$ ABC三个顶点的坐标分别为A(2，4)，B(1，1)，C(4，3)．

(1)、请画出 $△$ ABC关于原点对称的 $△$ A₁B₁C₁；

(2)、请画出 $△$ ABC绕点B逆时针旋转90°后的 $△$ A₂B₂C₂ ，并写出A₂的坐标．

查看试题解析
21. 如图，已知二次函数 $y = x^{2} - 2 x - 3$ 的图象与x轴交于点A、B ，与y轴交于点C ．

(1)、将 $y = x^{2} - 2 x - 3$ 化成 $y = a {(x - h)}^{2} + h$ 的形式；

(2)、求点A、B、C的坐标；

(3)、观察图象直接写出不等式 $x^{2} - 2 x - 3 > 0$ 的解集．

查看试题解析
22. 如图，某渔船向正东方向以12海里时的速度航行，在A处测得岛C在北偏东 $60 °$ 方向，1小时后渔船航行到B处，测得岛C在北偏东 $30 °$ 方向，已知该岛C上有一部信号发射塔，方圆20海里内的船只能够收到它发射的信号．

(1)、求B处离岛C的距离；

(2)、求该渔船在整个航行过程中收到岛C发射信号的时间．

查看试题解析
23. 先阅读材料，再解答问题：
小明同学在学习与圆有关的角时了解到：在同圆或等圆中，同弧（或等弧）所对的圆周角相等．如图1，点A，B ， C，D均为 $⊙ O$ 上的点，则有 $∠ C = ∠ D$ ．小明还发现，若点E在 $⊙ O$ 外，且与点D在直线 $A B$ 同侧，则有 $∠ D > ∠ E$ ．
请你参考小明得出的结论，解答下列问题：
问题：如图2，在平面直角坐标系 $x O y$ 中，点A的坐标为 $(0 ， 10)$ ，点B的坐标为 $(0 ， 4)$ ，点C的坐标为 $(2 ， 0)$ ．

(1)、在图2中作出 $△ A B C$ 的外接圆（保留必要的作图痕迹，不写作法），并求出此圆与x轴的另一个交点的坐标；

(2)、点P为x轴正半轴上的一个动点，连接 $A P$ 、 $B P$ ，当 $∠ A P B$ 达到最大时，直接写出此时点P的坐标．

查看试题解析
24. 某校九年级学习小组在探究学习过程中，用两块完全相同的且含60°角的直角三角板ABC与AFE按如图（1）所示位置放置，现将Rt△AEF绕A点按逆时针方向旋转角α（0°＜α＜90°），如图（2），AE与BC交于点M ， AC与EF交于点N ， BC与EF交于点P ．

(1)、求证：AM=AN；

(2)、当旋转角α=30°时，四边形ABPF是什么样的特殊四边形？并说明理由．

查看试题解析
25. 如图，在足够大的空地上有一段长为a米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，其中AD≤MN，已知矩形菜园的一边靠墙，另三边一共用了100米木栏．

(1)、若a=20，所围成的矩形菜园的面积为450平方米，求所利用旧墙AD的长；

(2)、求矩形菜园ABCD面积的最大值．

查看试题解析
26. 如图，在 $△ A B C$ 中，点O是 $A C$ 的中点，以O为圆心， $O A$ 为半径作 $⊙ O$ ，交 $B C$ 于点D ，交 $A B$ 于点E ，弧 $E D$ 与弧 $D C$ 相等，点F在线段 $B E$ 上， $∠ B A C = 2 ∠ B D F$ ．

(1)、求证： $A B = A C$ ；

(2)、判断 $D F$ 与 $⊙ O$ 的位置关系，并加以证明；

(3)、若 $⊙ O$ 的半径为5， $E B + D F = A O$ ，求 $B D$ 的长．

查看试题解析
27. 如图，在平面直角坐标系 $x O y$ 中，直线 $A B$ 的解析式为 $y = - \frac{3}{4} x + m$ ，与 $x$ 轴、 $y$ 轴分别交于点 $B$ 、点 $A$ ，抛物线 $y = a x^{2} + b x + 1$ 经过点 $A$ ，与直线 $A B$ 交于点 $C$ ，点 $C$ 的横坐标为 $4$ ，抛物线的对称轴为 $x = \frac{5}{4}$ ．

(1)、求抛物线的解析式；

(2)、动点 $P$ 在直线 $A C$ 上方的抛物线上，点 $P$ 的横坐标为 $t$ ，过点 $P$ 作 $x$ 轴的平行线交 $A C$ 于点 $M$ ，过点 $P$ 作 $y$ 轴的平行线交 $A C$ 于点 $N$ ，当 $A M = B N$ 时，求 $t$ 值；

(3)、点 $Q$ 是坐标平面内一点，将 $△ A O B$ 绕点 $Q$ 沿逆时针方向旋转 $90 °$ 后，得到 $△ A_{1} O_{1} B_{1}$ ，点 $A$ 、 $O$ 、 $B$ 的对应点分别是点 $A_{1}$ 、 $O_{1}$ 、 $B_{1}$ ．若 $△ A_{1} O_{1} B_{1}$ 的两个顶点恰好落在抛物线上，请直接写出此时点 $A_{1}$ 的横坐标．

查看试题解析