黑龙江省哈尔滨市呼兰区2023-2024学年九年级上学期数学第三次月考试卷
试卷更新日期:2023-12-26 类型:月考试卷
一、选择题(每题3分,计30分,每题只有一个正确的答案)
-
1. 下列函数中,是的反比例函数的是( )A、 B、 C、 D、2. 已知 , , , 则与的周长比值是( )A、2 B、4 C、 D、3. 生活中有许多对称美的图形,下列是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 反比例函数的图象在每个象限内,y随x的增大而增大,则m的取值范围是( )A、 B、 C、 D、5. 如图,AB为的直径,点C在上,且于点O , 弦CD与AB相交于点E , 若 , 则的度数为( )
4. 反比例函数的图象在每个象限内,y随x的增大而增大,则m的取值范围是( )A、 B、 C、 D、5. 如图,AB为的直径,点C在上,且于点O , 弦CD与AB相交于点E , 若 , 则的度数为( )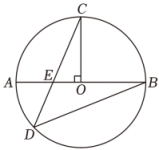 A、20° B、30° C、25° D、35°6. 电路上在电压保持不变的条件下,电流I(A)与电阻R(Ω)成反比例关系,I与R的函数图象如图,I关于R函数解析式是( )
A、20° B、30° C、25° D、35°6. 电路上在电压保持不变的条件下,电流I(A)与电阻R(Ω)成反比例关系,I与R的函数图象如图,I关于R函数解析式是( )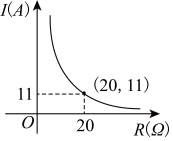 A、I= B、I=- C、I= D、I=7. 如图,某学生利用标杆测量一棵大树的高度,如果标杆的高为 , 并测得 , , 那么树的高度是( )
A、I= B、I=- C、I= D、I=7. 如图,某学生利用标杆测量一棵大树的高度,如果标杆的高为 , 并测得 , , 那么树的高度是( )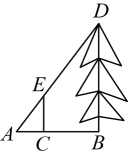 A、 B、 C、 D、8. 2023年是中国共产党建党102周年,全国各地积极开展“弘扬红色文化,重走长征路”主题教育活动,据了解,某展览中心3月份的参观人数为10万人,5月份的参观人数增加到万人,设参观人数的月平均增长率为x , 则可列方程为( )A、 B、 C、 D、9. 如图,点F时平行四边形的边上一点,直线交的延长线与点E , 则下列结论错误的是( )
A、 B、 C、 D、8. 2023年是中国共产党建党102周年,全国各地积极开展“弘扬红色文化,重走长征路”主题教育活动,据了解,某展览中心3月份的参观人数为10万人,5月份的参观人数增加到万人,设参观人数的月平均增长率为x , 则可列方程为( )A、 B、 C、 D、9. 如图,点F时平行四边形的边上一点,直线交的延长线与点E , 则下列结论错误的是( )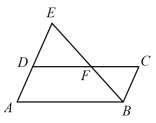 A、 B、 C、 D、10. 某星期日上午10:00,小淇从家匀速步行到附近的咖啡店看书,看完书后,他匀速跑步回家,且跑步的速度是步行速度的2倍,小淇离家的距离y(千米)与所用的时间x(分钟)之间(千米)的关系如图所示,下列说法正确的是( )
A、 B、 C、 D、10. 某星期日上午10:00,小淇从家匀速步行到附近的咖啡店看书,看完书后,他匀速跑步回家,且跑步的速度是步行速度的2倍,小淇离家的距离y(千米)与所用的时间x(分钟)之间(千米)的关系如图所示,下列说法正确的是( )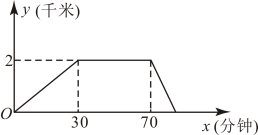 A、小淇在咖啡店看书的时间是分钟 B、小淇家与咖啡店的距离为4千米 C、小淇的步行速度是8千米/小时 D、小淇从咖啡厅回到家用时分钟
A、小淇在咖啡店看书的时间是分钟 B、小淇家与咖啡店的距离为4千米 C、小淇的步行速度是8千米/小时 D、小淇从咖啡厅回到家用时分钟二、填空题(每小题3分,共计30分)
-
11. 点关于原点对称的点 , 则 .12. 函数y=的自变量x的取值范围是 .
13. 反比例函数的图象经过点 , 则k的值为 .14. 如图,是的直径,弦 , 垂足为点 , 连接 , 若 , , 则等于 .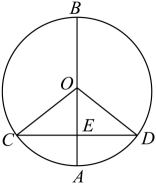 15. 二次函数的顶点坐标是 .16. 如图,在平面直角坐标系中,已知 , , 且与位似,原点O是位似中心,若的面积为 , 则的面积为 .
15. 二次函数的顶点坐标是 .16. 如图,在平面直角坐标系中,已知 , , 且与位似,原点O是位似中心,若的面积为 , 则的面积为 .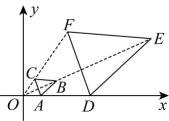 17. 已知扇形的圆心角度数为 , 弧长为 , 则该扇形的半径为 .18. 一个不透明的布袋里装有2个白球,1个黑球和1红球,它们除颜色外其余都相同.从中任意摸出1个球,不放回.再摸出1个球,则两次摸到的球都是白球的概率是 .19. 矩形的对角线 , 相交于点 , 点在矩形边上,连接 . 若 , , 则 .20. 如图,在正方形中,点E , F分别是上的点,相交于点L , , G为上一点,H为的中点.若 , , 连接 , 则线段的长度为 .
17. 已知扇形的圆心角度数为 , 弧长为 , 则该扇形的半径为 .18. 一个不透明的布袋里装有2个白球,1个黑球和1红球,它们除颜色外其余都相同.从中任意摸出1个球,不放回.再摸出1个球,则两次摸到的球都是白球的概率是 .19. 矩形的对角线 , 相交于点 , 点在矩形边上,连接 . 若 , , 则 .20. 如图,在正方形中,点E , F分别是上的点,相交于点L , , G为上一点,H为的中点.若 , , 连接 , 则线段的长度为 .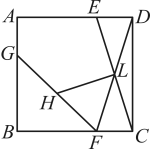
三、解答题:(共60分)
-
21. 先化简,再求值: , 其中 .22. 如图,方格纸中每个小正方形的边长均为1,线段和线段的端点均在小正方形的顶点上.
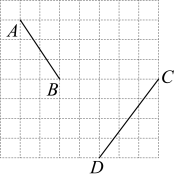
⑴在图中画出以为边的菱形 , 点E、F在小正方形的顶点上;
⑵在图中画出以为边的等腰三角形 , 点G在小正方形的顶点上,且的周长为 . 连接 , 请直接写出线段的长.
23. 如图,一次函数的图象与x轴、y轴分别交于点A , B , 与反比例函数的图象交于点 , .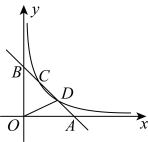 (1)、求出反比例函数的解析式与n的值;(2)、连接 , 求的面积.24. 如图1,已知四边形是菱形,点E在对角线上,点F在上,连接 , , .
(1)、求出反比例函数的解析式与n的值;(2)、连接 , 求的面积.24. 如图1,已知四边形是菱形,点E在对角线上,点F在上,连接 , , .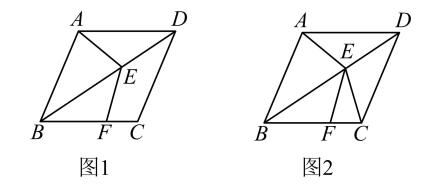 (1)、求证:;(2)、如图2,连接CE , 在不添加任何辅助线情况下,请直接写出图2中四个角(除外),使写出的每个角都与相等.25. 某书店在图书批发中心选购A , B两种科普书,A种科普书每本进价比B种科普书每本进价多20元,若用4800元购进A种科普书的数量是用1900元购进B种科普书数量的2倍.(1)、求A、B两种科普书每本进价各是多少元?(2)、该书店计划购进A、B两种科普书共60本,其中A种科普书每本售价为126元,B种科普书每本售价为85元,若A、B两种科普书全部售出,使总获利超过1380元,则至少购进A种科普书多少本?26. 如图1,内接于 , 于点D .
(1)、求证:;(2)、如图2,连接CE , 在不添加任何辅助线情况下,请直接写出图2中四个角(除外),使写出的每个角都与相等.25. 某书店在图书批发中心选购A , B两种科普书,A种科普书每本进价比B种科普书每本进价多20元,若用4800元购进A种科普书的数量是用1900元购进B种科普书数量的2倍.(1)、求A、B两种科普书每本进价各是多少元?(2)、该书店计划购进A、B两种科普书共60本,其中A种科普书每本售价为126元,B种科普书每本售价为85元,若A、B两种科普书全部售出,使总获利超过1380元,则至少购进A种科普书多少本?26. 如图1,内接于 , 于点D .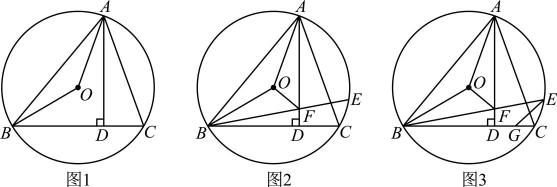 (1)、连接 , , 求证:;(2)、如图2,若点E为弧上一点,连接交于点F , 若 , , 连接 , 求证:平分;(3)、在(2)的条件下,如图3,点G为上一点,连接 , , 若 , , 求线段的长.27. 如图 , 在平面直角坐标系中,为坐标原点,已知抛物线的顶点的坐标为与轴交点的坐标为 .
(1)、连接 , , 求证:;(2)、如图2,若点E为弧上一点,连接交于点F , 若 , , 连接 , 求证:平分;(3)、在(2)的条件下,如图3,点G为上一点,连接 , , 若 , , 求线段的长.27. 如图 , 在平面直角坐标系中,为坐标原点,已知抛物线的顶点的坐标为与轴交点的坐标为 . (1)、求抛物线的解析式;(2)、如图 , 点为抛物线对称轴右侧抛物线上一点,连接 , , , 若设的面积为 , 点的横坐标为 , 求与的函数关系式(不要求写出自变量的取值范围);(3)、在(2)的条件下,如图 , 对称轴交于点 , 轴交延长线于点 , 垂足为 , 连接交轴于点 , 在的延长线上取点 , 连接使 , 若 , 求点的坐标.
(1)、求抛物线的解析式;(2)、如图 , 点为抛物线对称轴右侧抛物线上一点,连接 , , , 若设的面积为 , 点的横坐标为 , 求与的函数关系式(不要求写出自变量的取值范围);(3)、在(2)的条件下,如图 , 对称轴交于点 , 轴交延长线于点 , 垂足为 , 连接交轴于点 , 在的延长线上取点 , 连接使 , 若 , 求点的坐标.