四川省泸州市合江县2023-2024学年八年级上学期期中数学试题

试卷更新日期：2023-12-25 类型：期中考试

进入出卷网下载

一、选择题（本大题共12个小题，每小题3分，共36分）

1. 下列图形是杭州亚运会部分比赛项目的图标，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列长度的三条线段不能组成三角形的是（）

A、 $3 c m$ ， $4 c m$ ， $5 c m$ B、 $2 c m$ ， $2 c m$ ， $3 c m$ C、 $3 c m$ ， $3 c m$ ， $2 c m$ D、 $2 c m$ ， $3 c m$ ， $6 c m$

查看试题解析
3. 下列图中具有稳定性的是（）

A、 B、 C、 D、

查看试题解析
4. 在平面直角坐标系中，点 $P (4 ， 1)$ 关于 $y$ 轴对称的点的坐标是（）

A、 $(4 ， 1)$ B、 $(- 4 ， - 1)$ C、 $(- 4 ， 1)$ D、 $(4 ， - 1)$

查看试题解析
5. 如图，已知 $A B = D E ， A C = D F$ ，点B，E，C，F在一条直线上，若利用“ $S S S$ ”得到 $△ A B C ≌ △ D E F$ ，则需要添加的条件是（）

A、 $B E = E C$ B、 $E C = C F$ C、 $B E = C F$ D、 $D E = A C$

查看试题解析
6. 如图， $△ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ B A C$ ，过点 $D$ 作 $D E ⊥ A B$ 于 $E$ ，测得 $B C = 18$ ， $B E = 6$ ，则 $△ B D E$ 的周长是（）

A、30 B、24 C、18 D、12

查看试题解析
7. 已知等腰三角形的两条边长分别为5和9，则它的周长为（）

A、19 B、23 C、25 D、19或23

查看试题解析
8. 如图，直线 $m ∥ n$ ， $△ A B C$ 是直角三角形， $∠ B = 90 °$ ，点C在直线n上．若 $∠ 1 = 50 °$ ，则 $∠ 2$ 的度数是（）

A、60° B、50° C、45° D、40°

查看试题解析
9. 已知，如图， $△ A B C$ 中， $∠ A B C = 48 °$ ， $∠ A C B = 84 °$ ，点D、E分别在 $B A$ 、 $B C$ 延长线上， $B P$ 平分 $∠ A B C$ ， $C P$ 平分 $∠ A C E$ ，连接 $A P$ ，则 $∠ P A C$ 的度数为（　　）

A、45° B、48° C、60° D、66°

查看试题解析
10. 如图，在 $△ A B C$ 中， $∠ 1 = 120 °$ ， $∠ 2 = 50 °$ 将 $△ A B C$ 沿着直线 $l$ 叠，点 $C$ 落在点 $D$ 的位置，则 $∠ C$ 的度数是（）

A、 $40 °$ B、 $35 °$ C、 $50 °$ D、 $45 °$

查看试题解析
11. 已知，如图， $△ A B C$ 是等边三角形， $A E = C D$ ， $B Q ⊥ A D$ 于Q， $B E$ 交 $A D$ 于点P，下列说法：① $∠ B P Q = ∠ C = 60 °$ ， ② $A Q = B Q$ ， ③ $B P = 2 P Q$ ， ④ $A E + B D = A B$ ，其正确的个数有（）个

A、1 B、2 C、3 D、4

查看试题解析
12. 如图，在 $△ A B C$ 中， $A C = B C$ ， $A B = 6$ ， $△ A B C$ 的面积为12， $C D ⊥ A B$ 于点 $D$ ，直线 $E F$ 垂直平分 $B C$ 交 $A B$ 于点 $E$ ，交 $B C$ 于点 $F$ ， $P$ 是线段 $E F$ 上的一个动点，分别连接 $B P$ ， $P D$ ，则 $△ P B D$ 的周长的最小值是（）

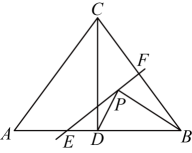A、6 B、7 C、10 D、12

查看试题解析

二、填空题（本大题共4个小题，每小题3分，共12分）

13. 如图， $△ A B C ≌ △ F D E$ ， $A B = F D ， B C = D E ， A E = 20 c m ， F C = 10 c m$ ，则 $A F$ 的长是 $c m$ ．

查看试题解析
14. 若点 $A (a ， 3)$ 与 $B (2 ， b)$ 关于x轴对称，则点 $M (a ， b)$ 在第象限．

查看试题解析
15. 如果正多边形的每一个内角都为108°，那么它的边数是．

查看试题解析
16. 如图，A、B、C在同一条直线上， $△ A B F$ 和 $△ B C E$ 均为等边三角形， $A E$ 、 $F C$ 分别交 $F B$ 、 $E B$ 于点M、N，下列结论中：① $△ A B E ≌ △ F B C$ ， ② $A B = F N$ ， ③ $B M = B N$ ， ④ $∠ A D F = 60 °$ ， ⑤ $D B$ 平分 $∠ A D C$ ，其中正确的有．（填序号）

查看试题解析

三、解答题（本大题共3个小题，每小题6分，共18分）

17. 已知一个 $n$ 边形的每一个内角都等于 $150 °$ ，求这个 $n$ 边形的内角和．

查看试题解析
18. 如图， $A F = D C$ ， $E F = B C$ ， $A B = E D$ ，证明 $△ A B C ≌ △ D E F$ ．

查看试题解析
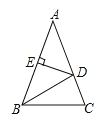
19.
如图，△ABC中，AB=AC，∠A=40°，DE是腰AB的垂直平分线，求∠DBC的度数．

查看试题解析

四、解答题（本大题共2个小题，每小题7分，共14分）

20. 已知：如图，已知 $△ A B C$ 中，其中 $A (0 ， - 2)$ ， $B (2 ， - 4)$ ， $C (4 ， - 1)$ ．

(1)、画出与 $△ A B C$ 关于y轴对称的图形 $△ A_{1} B_{1} C_{1}$ ；

(2)、写出 $△ A_{1} B_{1} C_{1}$ 各顶点坐标；

(3)、求 $△ A B C$ 的面积．

查看试题解析
21. 尺规作图（不写作法，保留作图痕迹）：

(1)、如图①，要在河边l修建一个水泵站M，使 $M A = M B$ ．水泵站M要建在什么位置？

(2)、如图②，三条公路两两相交，现计划修建一个油库P，要求油库P到这三条公路的距离都相等，那么如何选择油库P的位置？（请作出符合条件的一个）

查看试题解析

五、解答题（本大题共2个小题，每小题8分，共16分）

22. 如图所示，已知 $∠ B = ∠ C = 90 °$ ， $M$ 是 $B C$ 的中点， $D M$ 平分 $∠ A D C$ .

求证：

(1)、 $A M$ 平分 $∠ D A B$ ；

(2)、 $A D = A B + C D$ .

查看试题解析
23. 设a，b，c是 $△ A B C$ 的三边，

(1)、化简 $| a - b - c | + | b + c - a | - | c - a - b |$

(2)、若b，c满足 ${(b - 2)}^{2} + | c - 3 | = 0$ ，且a为方程 $| x - 4 | = 2$ 的解，判断 $△ A B C$ 的形状并说明理由．

查看试题解析

六、解答题（本大题共2个小题，每小题12分，共24分）

24. 如图，△ABC是等边三角形，AB=6，P是AC边上一动点，由A向C运动（与A、C不重合），Q是CB延长线上一动点，与点P同时以相同的速度由B向CB延长线方向运动（Q不与B重合），过P作PE⊥AB于E，连接PQ交AB于D．

(1)、当∠BQD=30°时，求AP的长；

(2)、证明：在运动过程中，点D是线段PQ的中点．

查看试题解析
25. 如图， $P$ 为等边 $△ A B C$ 的边 $B C$ 延长线上的一动点，以 $A P$ 为边向上作等边 $△ A P D$ ，连接 $C D$ ．

(1)、求证： $△ A B P ≌ △ A C D$ ；

(2)、当 $P C = A C$ 时，求 $∠ P D C$ 的度数；

(3)、 $∠ P D C$ 与 $∠ P A C$ 有怎样的数量关系？随着点 $P$ 位置的变化， $∠ P D C$ 与 $∠ P A C$ 的数量关系是否会发生变化？请说明理由．

查看试题解析