山东省济南市历下区2023-2024学年九年级上学期数学期中考试试卷

试卷更新日期：2023-12-25 类型：期中考试

进入出卷网下载

一、选择题（本大题共10个小题，每小题4分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的．）

1. 一个几何体如图水平放置，它的俯视图是（）

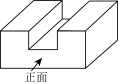A、 B、 C、 D、

查看试题解析
2. 如图，在Rt△ABC中， $∠ C = 90 °$ ， $A C = 4$ ， $B C = 3$ ，则∠A的正切值是（）

A、 $\frac{3}{5}$ B、 $\frac{4}{3}$ C、 $\frac{3}{4}$ D、 $\frac{4}{5}$

查看试题解析
3. 如图，两条直线被三条平行线所截，若 $A B ： B C = 2 ： 3$ ， $D E = 4$ ，则EF为（）

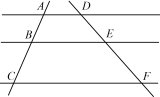A、5 B、6 C、7 D、8

查看试题解析
4. 如图，小明同学利用相似三角形测量旗杆的高度，若测得木杆AB长2m，它的影长BC为1m，旗杆DE的影长EF为6m，则旗杆DE的高度为（）

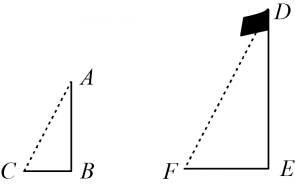A、9m B、10m C、11m D、12m

查看试题解析
5. 已知点 $A (- 2 ， y_{1})$ ， $B (2 ， y_{2})$ ， $C (4 ， y_{3})$ 都在反比例函数 $y = \frac{8}{x}$ 的图象上，则 $y_{1} ， y_{2} ， y_{3}$ 的大小关系为（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{1} < y_{3} < y_{2}$ C、 $y_{3} < y_{2} < y_{1}$ D、 $y_{2} < y_{3} < y_{1}$

查看试题解析
6. 围棋起源于中国，棋子分黑白两色．一个不透明的盒子中装有2个黑色棋子和1个白色棋子，每个棋子除颜色外都相同．从中随机摸出一个棋子，记下颜色后放回，再从中随机摸出一个棋子，则两次摸到相同颜色的棋子的概率是（）

A、 $\frac{4}{9}$ B、 $\frac{1}{2}$ C、 $\frac{5}{9}$ D、 $\frac{2}{3}$

查看试题解析
7. 一次函数 $y = - a x + a$ 与反比例函数 $y = \frac{a}{x}$ 在同一平面直角坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析
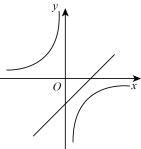8. 如图，在边长都为1的方格纸上，小明同学绘制了艺术字体“A”，已知点O ， M ， N都在格点上，点P ， Q在格线上，则点P与点Q之间的距离为（）

A、5 B、 $\sqrt{10}$ C、 $\frac{9}{2}$ D、 $\frac{14}{3}$

查看试题解析
9. 如图，在Rt△ABC中， $∠ A C B = 90 °$ ， $B C = \sqrt{5}$ ，点D为边AB上一点，将△BCD沿CD折叠，点B恰好落在边AB上的点E处．若 $A E = 3$ ，则BD为（）

A、 $\frac{\sqrt{5}}{3}$ B、1 C、 $\frac{\sqrt{5}}{2}$ D、 $\frac{4}{3}$

查看试题解析
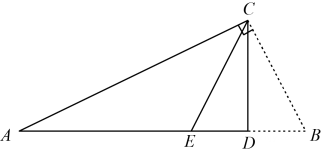10. 定义：在平面直角坐标系中，对于点 $P (x_{1} ， y_{1})$ ，当点 $Q (x_{2} ， y_{2})$ 满足 $2 (x_{1} + x_{2}) = y_{1} + y_{2}$ 时，称点 $Q (x_{2} ， y_{2})$ 是点 $P (x_{1} ， y_{1})$ 的“倍增点”．在平面直角坐标系中，若反比例函数 $y = \frac{4}{x}$ 图象上的点A与点B都是点 $P_{1} (1 ， 0)$ 的“倍增点”，连接OA ， OB ， AB ，则△OAB的面积为（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题（本大题共6个小题，每小题4分，共24分．）

11. 已知点 $(1 ， 2)$ 在反比例函数 $y = \frac{k}{x}$ 上，则 $k =$ ．

查看试题解析
12. 已知 $\frac{a}{b} = \frac{c}{d} = \frac{2}{3} (b + d \neq 0)$ ，则 $\frac{a + c}{b + d} =$ ．

查看试题解析
13. 为了估计鱼塘中的鱼数，养鱼者首先从鱼塘中打捞20条鱼，在每一条鱼身上做好记号后把这些鱼放归鱼塘，再从鱼塘中打捞500条鱼。如果在这500条鱼中有5条鱼是有记号的，那么估计鱼塘中鱼的条数为条．

查看试题解析
14. 2023年第19届杭州亚运会的会徽“潮涌”将自然奇观与人文精神进行巧妙融合，其中浪潮设计借助了黄金分割比以给人协调的美感。如图，若点C可看做是线段AB的黄金分割点（ $A C < C B$ ）， $A B = 10$ cm，则 $B C =$ cm．（结果保留根号）

查看试题解析
15. 如图，反比例函 $y = - \frac{\sqrt{3}}{x}$ 的图象经过菱形OABC的顶点A ，点B在y轴上，过点B作y轴的垂线与反比例函数的图象相交于点D ．若 $∠ B A O = 60 °$ ，则点D的坐标是．

查看试题解析
16. 如图，在矩形ABCD中，DE平分∠ADC ，交BC于点E ， $E F ⊥ A E$ ，交CD于点F ，以AE ， EF为边，作矩形AEFG ， FG与DA相交于点H ．若 $C E = 3$ ， $A H = 4$ ，则 $A E =$ ．

查看试题解析

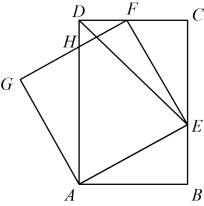
三、解答题（本大题共10个小题，共86分．请写出文字说明、证明过程或演算步骤。）

17. 计算：

(1)、 $2 s i n 60 ° + t a n 45 °$

(2)、 $c o s^{2} 30 ° - s i n^{2} 45 °$

查看试题解析
18. 如图，小树AB在路灯O的照射下形成投影BC ．

(1)、此光源下形成的投影属于．（填“平行投影”或“中心投影”）

(2)、已知树高AB为2m，树影BC为3m，树与路灯的水平距离BP为4.5m．求路灯的高度OP ．

查看试题解析
19. 如图，AB、CD相交于点O ，已知 $O A = 6$ ， $O D = 8$ ， $O B = 4$ ， $O C = 3$ ，求证： $∠ B = ∠ D$ ．

查看试题解析
20. 如图，在平面直角坐标系中，以原点O为位似中心，五边形OABCD的五个顶点坐标分别为 $O (0 ， 0)$ ， $A (- 1 ， 3)$ ， $B (1 ， 4)$ ， $C (4 ， 2)$ ， $D (3 ， 0)$ ．

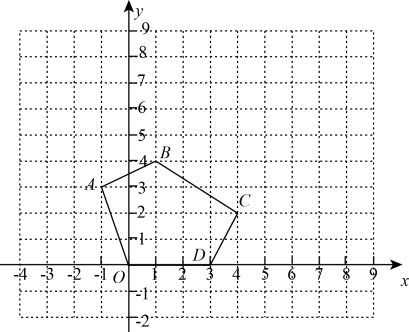(1)、以原点O为位似中心，在原点O的同侧作五边形OABCD的位似图形 $O A_{1} B_{1} C_{1} D_{1}$ ，使它与五边形OABCD的相似比为2：1．

(2)、写出 $C_{1}$ 的坐标．

(3)、已知五边形OABCD的面积为13.5，则五边形 $O A_{1} B_{1} C_{1} D_{1}$ 的面积为．

查看试题解析
21. 九年级组织“11·9全国消防日”消防安全知识竞赛活动，其中本次竞赛成绩分为“优秀”“良好”“一般”“较差”四个等级，为了解全体九年级同学的消防安全知识水平，随机抽取了m个同学的竞赛成绩进行统计整理，根据成绩绘制成如下两幅不完整的统计图：
请结合以上信息完成下列问题：

(1)、 $m =$ ．

(2)、如果九年级共有600名学生参加本次活动，那么可估计竞赛成绩为“优秀”的学生有人．

(3)、此次活动中有五名同学获得满分，其中有三名女生和两名男生．现从这五名同学中随机挑选两名同学参加校外比赛，请用列表法或画树状图法求出选中的两名同学恰好是一男一女的概率．

查看试题解析
22. 为确保身体健康，自来水最好烧开（加热到100℃）后再饮用．某款家用饮水机，具有加热、保温等功能．现将20℃的自来水加入到饮水机中，先加热到100℃．此后停止加热，水温开始下降，达到设置的饮用温度后开始保温．比如事先设置饮用温度为50℃，则水温下降到50℃后不再改变，此时可以正常饮用．整个过程中，水温y（℃）与通电时间x（min）之间的函数关系如图所示．

(1)、水温从20℃加热到100℃，需要min；请直接写出加热过程中水温y与通电时间x之间的函数关系式：．

(2)、观察判断：在水温下降过程中，y与x的函数关系是函数，并尝试求该函数的解析式．

(3)、已知冲泡奶粉的最佳温度在40℃左右，某家庭为了给婴儿冲泡奶粉，将饮用温度设置为40℃．现将20℃的自来水加入到饮水机中，此后开始正常加热．则从加入自来水开始，需要等待多长时间才可以接水冲泡奶粉？

查看试题解析
23. 在“济南天下第一泉”风景区随处可以看到历代名人雅士留下的匾额和楹联，它们丰富了园林的人文内涵．如图1，趵突泉公园南门上悬挂着的匳额，图2中的线段AB就是这块匾额的截面示意图．已知 $A B = 0.8$ 米， $∠ D A B = 37 °$ ．从水平地面点C处看点B ，仰角 $∠ M C D = 45 °$ ，且视线经过射线MA上的点D ，从点E处看点A ， $∠ A E M = 53 °$ ．且 $C E = 2.07$ 米．（参考数据： $s i n 37 ° \approx \frac{3}{5} ， c o s 37 ° \approx \frac{4}{5} ， t a n 37 ° \approx \frac{3}{4}$ ）

(1)、求点B到AD的水平距离．

(2)、求线段DA的长．

(3)、求匾额上点A到地面的距离AM的长．

查看试题解析
24. 如图，正比例函数 $y = k x$ 的图象与反比例函数 $y = \frac{m}{x}$ 的图象交于A ， B两点，其中 $A (- 4 ， 3)$ ．

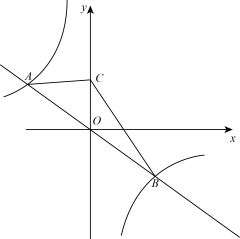(1)、求k ， m的值．

(2)、根据函数图象，直接写出不等式 $k x - \frac{m}{x} \leq 0$ 的解集．

(3)、若点C在y轴上，且△ABC的面积为16，求点C的坐标。

查看试题解析
25.

(1)、【问题情境】如图1，小明把三角板EFG（ $∠ G F E = 30 °$ ）放置到矩形ABCD中，使得顶点E、F、G分别落在AD、CD、AB上，你发现线段ED与AG有什么数量关系？
直接写出结论：（不用证明）．

(2)、【变式探究】如图2，小明把三角板EFG（ $∠ G F E = 30 °$ ）放置到矩形ABCD中，使得顶点E、F、G分别在AD、BC、AB边上，若 $G A = 4$ ， $A E = 6$ ，求BG的长．

(3)、【拓展应用】如图3，小明把三角形EFG放置到平行四边形ABCD中，使得顶点E、F、G分别落在AD、BC、AB边上，若 $\frac{A B}{A D} = \frac{4}{5}$ ， $\frac{A E}{A D} = \frac{3}{10}$ ， $∠ F E G = ∠ B A D$ ，求出 $\frac{E G}{E F}$ 的值．

查看试题解析
26. 小静发现希腊数学家曾利用反比例函数图象将一个角三等分，具体方法如下：
第一步：建立平面直角坐标系，将已知锐角∠AOB的顶点与原点O重合，角的一边OB与x轴正方向重合．在平面直角坐标系里，绘制函数 $y = \frac{1}{x}$ 的图象，图象与已知角的另一边OA交于点P ．
第二步：以P为圆心、以20P为半径作弧，交函数 $y = \frac{1}{x}$ 的图象于点R ．
第三步：分别过点P和R作x轴和y轴的平行线，两线相交于点M ，连接OM ，得到∠MOB（如图1）．
这时 $∠ M O B = \frac{1}{3} ∠ A O B$ ．
为什么 $∠ M O B = \frac{1}{3} ∠ A O B$ ？小静想要证明这个结论却没有思路，便询问老师．
老师进行了指导：分别过点P和R作y轴和x轴的平行线，两线交于点Q（如图2），解答这道题的关键就是证明O ， Q ， M三点共线，在平面直角坐标系中，证明三点共线最直接的做法是先用两点确定一条直线的表达式，再证明第三点在这条直线上．
老师指导后，小静若有所思．请你和小静一起，完成下列问题．
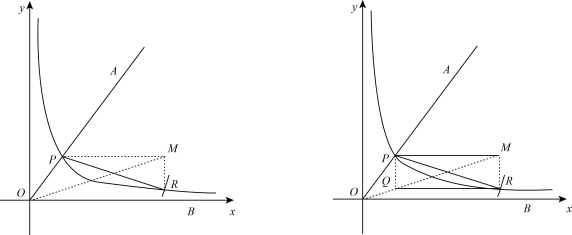
图1 图2

(1)、已知 $C (- 1 ， 0)$ ， $D (0 ， 2)$ ， $E (1 ， 4)$ ，请说明C、D、E三点共线．

(2)、在“三等分角”的作图中（如图2），请证明O ， Q ， M三点共线．

(3)、在（2）的基础上，请证明 $∠ M O B = \frac{1}{3} ∠ A O B$ ．

查看试题解析