山东省济南市历下区2023-2024学年七年级上学期数学期中考试试卷
试卷更新日期:2023-12-25 类型:期中考试
一、选择题(本大题共10小题,每小题4分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
-
1. 的相反数是( )A、 B、 C、5 D、2. 在中,负数共有( )A、2个 B、3个 C、4个 D、5个3. 杭州奥体中心体育场又称“大莲花”,为杭州第19届亚运会主会场.座席数为80800个.将数据80800用科学记数法表示为( )A、 B、 C、 D、4. 下列四个数中,最小的是( )A、 B、 C、 D、5. 下列图形中,能够折叠成一个正方体的是( )A、
 B、
B、 C、
C、 D、
D、 6. 已知有理数 , 在数轴上的位置如图所示,则 , , , 从大到小的顺序为( )
6. 已知有理数 , 在数轴上的位置如图所示,则 , , , 从大到小的顺序为( ) A、 B、 C、 D、7. 用一平面去截下列几何体,其截面可能是长方形的有( )
A、 B、 C、 D、7. 用一平面去截下列几何体,其截面可能是长方形的有( )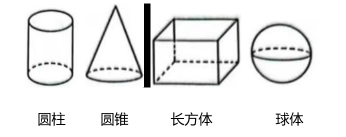 A、1个 B、2个 C、3个 D、4个8. 下列运算正确的是( )A、 B、 C、 D、9. 某商店出售一种商品,有以下几种方案,调价后价格最低的方案是( )A、先提价 , 再降价 B、先降价 , 再提价 C、先提价 , 再降价 D、先提价 , 再降价10. 如图,将一张长方形的纸对折,可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕.想象一下,如果对折次,可以得到折痕的条数是( )
A、1个 B、2个 C、3个 D、4个8. 下列运算正确的是( )A、 B、 C、 D、9. 某商店出售一种商品,有以下几种方案,调价后价格最低的方案是( )A、先提价 , 再降价 B、先降价 , 再提价 C、先提价 , 再降价 D、先提价 , 再降价10. 如图,将一张长方形的纸对折,可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕.想象一下,如果对折次,可以得到折痕的条数是( )


第一次对折 第二次对折 第三次对折
A、 B、 C、 D、二、填空题(本大题共6个小题,每小题4分,共24分.)
-
11. 朱自清的《春》中有描写春雨“像牛毛、像花针、像细丝,密密麻麻地斜织着”的语句,这里把雨看成了线,这种现象可以用数学知识解释为 .12. 单项式的次数是 .13. 杭州亚运会于2023年10月顺利落幕,中国队获金牌和奖牌榜双第一,如图是一个正方体的表面展开图,与“亚”字相对面上的汉字是 .
 14. 若 , 则的值为.15. 若 , 则代数式的值为 .16. 如图,将两张边长分别为5和4的正方形纸片分别按图①和图②两种方式放置在长方形内(图①和图②中两张正方形纸片均有部分重叠),未被这两张正方形纸片覆盖的部分用阴影表示.若长方形中边 , 的长度分别为 . 设图①中阴影部分面积为 , 图②中阴影部分面积为 , 当时,的值为 .
14. 若 , 则的值为.15. 若 , 则代数式的值为 .16. 如图,将两张边长分别为5和4的正方形纸片分别按图①和图②两种方式放置在长方形内(图①和图②中两张正方形纸片均有部分重叠),未被这两张正方形纸片覆盖的部分用阴影表示.若长方形中边 , 的长度分别为 . 设图①中阴影部分面积为 , 图②中阴影部分面积为 , 当时,的值为 .
三、解答题(本大题共10个小题,共86分.请写出文字说明、证明过程或演算步骤.)
-
17.(1)、;(2)、 .18.(1)、;(2)、 .19.
先化简,再求值: , 其中 .
20. 如图是由一些相同的小正方体组成的几何体.从正面看
 从正面看
从正面看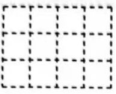 从左面看
从左面看 从上面看
从上面看 (1)、请在指定位置画出该几何体从正面、左面和上面看到的形状图;(2)、在这个几何体上再添加一些相同的小正方体,如果从左面和从上面看到的形状图不变,那么最多可以再添加个小正方体.21. 气候变暖导致全球大部分地区极端强降水事件增多,由此引发的洪涝等灾害风险已倍受各界广泛关注.为揭示气候变暖背景下极端降水的变化规律,查阅山东省气象信息中心1961——2020年降水量资料发现,夏季出现极端降水次数最多.(1)、若设定100次为标准次数,试完成表1:
(1)、请在指定位置画出该几何体从正面、左面和上面看到的形状图;(2)、在这个几何体上再添加一些相同的小正方体,如果从左面和从上面看到的形状图不变,那么最多可以再添加个小正方体.21. 气候变暖导致全球大部分地区极端强降水事件增多,由此引发的洪涝等灾害风险已倍受各界广泛关注.为揭示气候变暖背景下极端降水的变化规律,查阅山东省气象信息中心1961——2020年降水量资料发现,夏季出现极端降水次数最多.(1)、若设定100次为标准次数,试完成表1: (2)、极端降水出现次数最多的地区与最少的地区相差次;(3)、以上地区出现极端降水的平均次数是多少?22. 书籍是人类进步的阶梯!为爱护书本我们一般都会将书本用包书纸包好.现有一本如图所示的数学课本,长为、宽为、厚为 , 小海打算用一张长方形包书纸包好这本数学书.第一步,他将包书纸沿虚线折出折痕,封面和封底各折进去;第二步,将阴影部分沿虚线剪掉,请帮助小海解决以下问题:
(2)、极端降水出现次数最多的地区与最少的地区相差次;(3)、以上地区出现极端降水的平均次数是多少?22. 书籍是人类进步的阶梯!为爱护书本我们一般都会将书本用包书纸包好.现有一本如图所示的数学课本,长为、宽为、厚为 , 小海打算用一张长方形包书纸包好这本数学书.第一步,他将包书纸沿虚线折出折痕,封面和封底各折进去;第二步,将阴影部分沿虚线剪掉,请帮助小海解决以下问题:
 (1)、小海第一步中所用的长方形包书纸周长是多少厘米?(用含的代数式表示)(2)、若封面和封底沿虚线各折进去 , 剪掉阴影部分后,包书纸的面积是多少?23. 校运动会,小明负责在一条东西赛道上为同学们拍照,这天他从主席台出发,最后停留在处.规定以向东的方向为正方向,步行记录如下(单位:米):
(1)、小海第一步中所用的长方形包书纸周长是多少厘米?(用含的代数式表示)(2)、若封面和封底沿虚线各折进去 , 剪掉阴影部分后,包书纸的面积是多少?23. 校运动会,小明负责在一条东西赛道上为同学们拍照,这天他从主席台出发,最后停留在处.规定以向东的方向为正方向,步行记录如下(单位:米): (1)、小明离主席台最远是米;(2)、以主席台为原点,用1个单位长度表示 , 请在数轴上表示点;(3)、在主席台东边5米处是仲裁处,小明经过仲裁处次;(4)、若小明每步行1米消耗0.04卡路里,那么他在拍照过程中步行消耗的卡路里是多少?24. 随着生活水平的日益提高,人们的健康意识逐渐增强,越来越多的人把健身作为一种时尚的生活方式,某商家抓住机遇推出促销活动,向客户提供了两种优惠方案:
(1)、小明离主席台最远是米;(2)、以主席台为原点,用1个单位长度表示 , 请在数轴上表示点;(3)、在主席台东边5米处是仲裁处,小明经过仲裁处次;(4)、若小明每步行1米消耗0.04卡路里,那么他在拍照过程中步行消耗的卡路里是多少?24. 随着生活水平的日益提高,人们的健康意识逐渐增强,越来越多的人把健身作为一种时尚的生活方式,某商家抓住机遇推出促销活动,向客户提供了两种优惠方案:方案一:买一件运动外套送一件卫衣;
方案二:运动外套和卫衣均在定价的基础上打8折.
运动外套每件定价300元,卫衣每件定价100元.在开展促销活动期间,某俱乐部要到该商场购买运动外套100件,卫衣件().
(1)、方案一需付款:元,方案二需付款:元;(2)、当时,请计算并比较这两种方案哪种更划算;(3)、当时,如果两种方案可以组合使用,你能帮助俱乐部设计一种最省钱的方案吗?请直接写出你的方案.25. 【阅读】可理解为数轴上表示所对应的点与所对应的点之间的距离;
如可理解为数轴上表示6所对应的点与2所对应的点之间的距离;
可以看作 , 可理解为数轴上表示6所对应的点与所对应的点之间的距离;
【探索】
回答下列问题:
(1)、可理解为数轴上表示所对应的点与所对应的点之间的距离.(2)、若 , 则数 .(3)、若 , 则数 .(4)、如图所示,在数轴上,若点表示的数记为两点的距离为8,且点在点的右侧,现有一点以每分钟2个单位长度的速度从点向右出发,点以每分钟1个单位长度的速度从点向右出发,求分钟后点与点的距离.(结果用含的代数式表示,并化到最简) 26. 【概念学习】
26. 【概念学习】定义新运算:求若干个相同的非零有理数的商的运算叫做除方.比如,类比有理数的乘方,我们把写作 , 读作“2的圈3次方”;写作 , 读作“的圈4次方”.一般地,把记作; , 读作“的圈次方”.特别地,规定: .
(1)、【初步探究】直接写出计算结果: , ;(2)、若为任意正整数,下列关于除方的说法中,正确的有;(填写正确的序号)①任何非零数的圈2次方都等于1;
②任何非零数的圈3次方都等于它的倒数;
③圈次方等于它本身的数是1或;
④负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数.
(3)、请把有理数的圈次方写成幂的形式:;(4)、计算: .