山西省太原市2023-2024学年八年级上学期数学期中考试试卷
试卷更新日期:2023-12-25 类型:期中考试
一、选择题(本大题共10个小题.在每小题给出的四个选项中,只有一项符合题目要求,请将其字母序号填入下表相应位置)
-
1. 有理数16的算术平方根是( )A、8 B、±8 C、4 D、±42. 下列各点,位于第三象限的是( )A、 B、 C、 D、3. 如图,用两个边长为1的小正方形拼成一个大正方形,则下列关于大正方形边长的说法正确的是( )
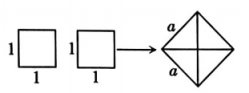 A、是整数 B、满足 C、是分数 D、是无理数4. 现有长度为4cm,5cm,8cm,12cm,13cm的五根细木条,若选择其中的三根首尾顺次相接,恰好能摆成直角三角形的是( )A、4cm,5cm,8cm B、5cm,8cm,12cm C、5cm,12cm,13cm D、8cm,12cm,13cm5. 下列运算正确的是( )A、 B、 C、 D、6. 在学习勾股定理时,小明利用如图验证了勾股定理.若图中 , , 则阴影部分直角三角形的面积为( )
A、是整数 B、满足 C、是分数 D、是无理数4. 现有长度为4cm,5cm,8cm,12cm,13cm的五根细木条,若选择其中的三根首尾顺次相接,恰好能摆成直角三角形的是( )A、4cm,5cm,8cm B、5cm,8cm,12cm C、5cm,12cm,13cm D、8cm,12cm,13cm5. 下列运算正确的是( )A、 B、 C、 D、6. 在学习勾股定理时,小明利用如图验证了勾股定理.若图中 , , 则阴影部分直角三角形的面积为( )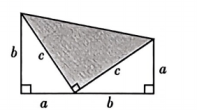 A、5 B、25 C、 D、7. 将化成最简二次根式的结果为( )A、 B、 C、 D、8. 将所有满足关系式的 , 的值作为点的坐标 , 这些点在平面直角坐标系中组成的图形可能是( )A、
A、5 B、25 C、 D、7. 将化成最简二次根式的结果为( )A、 B、 C、 D、8. 将所有满足关系式的 , 的值作为点的坐标 , 这些点在平面直角坐标系中组成的图形可能是( )A、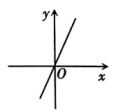 B、
B、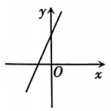 C、
C、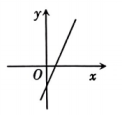 D、
D、 9. 如图的数轴上,点 , 对应的实数分别为1,3,线段于点 , 且长为1个单位长度.若以点为圆心,长为半径的弧交数轴于0和1之间的点 , 则点表示的实数为( )
9. 如图的数轴上,点 , 对应的实数分别为1,3,线段于点 , 且长为1个单位长度.若以点为圆心,长为半径的弧交数轴于0和1之间的点 , 则点表示的实数为( )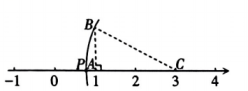 A、 B、 C、 D、10. 若点 , , 在一次函数(是常数)的图象上,则 , , 的大小关系是( )A、 B、 C、 D、
A、 B、 C、 D、10. 若点 , , 在一次函数(是常数)的图象上,则 , , 的大小关系是( )A、 B、 C、 D、二、填空题(本大题共5个小题.把答案写在题中横线上)
-
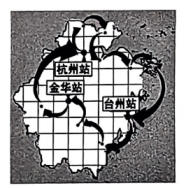
11. 化简的结果是.12. 如图是杭州第19届亚运会火炬传递路线示意图.若以“杭州站”为原点建立平面直角坐标系,“金华站”的坐标可表示为 , 则“台州站”的坐标可表示为.
 13. 已知正比例函数的图象经过点 , 则此正比例函数的表达式为.14. 如图,在中, , , , 若的平分线交于点 , 则的长为.
13. 已知正比例函数的图象经过点 , 则此正比例函数的表达式为.14. 如图,在中, , , , 若的平分线交于点 , 则的长为. 15. 包装纸箱是我们生活中常见的物品.如图1,创意DIY小组的同学将一个的长方体纸箱裁去一部分(虚线为裁剪线),得到图2所示的简易书架.若一只蜘蛛从该书架的顶点出发,沿书架内壁爬行到顶点处,则它爬行的最短距离为cm.
15. 包装纸箱是我们生活中常见的物品.如图1,创意DIY小组的同学将一个的长方体纸箱裁去一部分(虚线为裁剪线),得到图2所示的简易书架.若一只蜘蛛从该书架的顶点出发,沿书架内壁爬行到顶点处,则它爬行的最短距离为cm.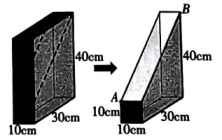
三、解答题(本大题共8个小题.解答应写出必要的文字说明、演算步骤或推理过程)
-
16. 计算下列各题:(1)、;(2)、;(3)、;(4)、.17. 在如图所示的平面直角坐标系中,线段的两个端点 , 的坐标分别为 , , 点在轴负半轴上,且到轴的距离为2个单位长度.
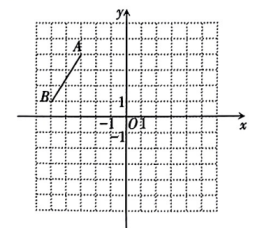
⑴请在图中标出点的位置;
⑵将点 , 的纵坐标分别乘-1,横坐标不变,得到点 , , 请在图中画出;
⑶请在图中画出 , 使它与(2)中得到的关于轴对称.若点是线段上的任意一点,则点在上的对应点的坐标为 .
18. 北京时间10月2日,在杭州亚运会女子撑杆跳高决赛中,李玲刷新了由个人保持的赛会纪录,以4米63夺冠,实现了个人亚运会三连冠.据研究,撑杆跳高运动员起跳后身体重心提高的高度(米)与其起跳速度(米/秒)之间满足(其中米/秒).若某运动员在训练中要使起跳后身体重心提高4米,则其起跳时的速度应为多少?( , 结果保留整数) 19. 如图,已知等边顶点 , 的坐标分别为 , , 且顶点在第一象限,求点的坐标.
19. 如图,已知等边顶点 , 的坐标分别为 , , 且顶点在第一象限,求点的坐标.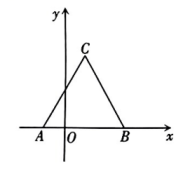 20. 清德铺位于清徐县徐沟镇正南5公里,该村种植红薯由来已久,据传从清光绪时就开始享誉龙城,2018年获国家农产品地理标志登记保护.红薯丰收时节,某农户启动线上销售,每千克红薯的定价为3元,当销售量不超过10千克时,每笔订单均收取6元的快递费;当销售量超过10千克时,免快递费.设每笔线上红薯订单的销售量为千克,每笔订单的总收款额为元.
20. 清德铺位于清徐县徐沟镇正南5公里,该村种植红薯由来已久,据传从清光绪时就开始享誉龙城,2018年获国家农产品地理标志登记保护.红薯丰收时节,某农户启动线上销售,每千克红薯的定价为3元,当销售量不超过10千克时,每笔订单均收取6元的快递费;当销售量超过10千克时,免快递费.设每笔线上红薯订单的销售量为千克,每笔订单的总收款额为元. (1)、当时,与之间的函数关系式为;
(1)、当时,与之间的函数关系式为;当时,与之间的函数关系式为;
(2)、一笔10千克的线上红薯订单,总收款额为多少元?(3)、若一笔订单的总收款额为108元,求这笔订单的销售量.21. 校园内有一处池塘,数学实践小组的同学想利用所学知识测量池塘两端 , 两点之间的距离,他们的操作过程如下:①沿延长线的方向,在池塘边的空地上选点 , 使米;②在的一侧选点 , 恰好使米,米;③测得米.请根据他们的操作过程,求出 , 两点间的距离. 22. 阅读下列材料,解答相应的问题:
22. 阅读下列材料,解答相应的问题:研究函数的图象一般要研究其形状、位置、图象特征(如对称性).借助图象我们可以直观地得到函数的性质.例如,在研究正比例函数的图象时,通过列表、描点、连线等步骤,得到如下结论:①的图象是经过原点的一条直线;②的图象经过坐标系的第一、三象限.小文借鉴研究正比例函数的经验,对新函数的图象展开探究,过程如下.
①根据函数表达式列表:
...
-3
-2
-1
0
1
2
3
...
...
0
2
4
6
...
②在如图所示的坐标系中描点、连线,画出函数的图象.

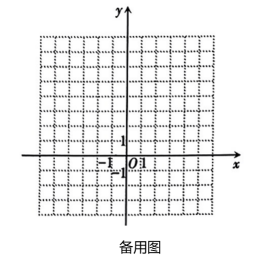 (1)、请你将小文列表、描点、连线的过程补充完整;(2)、请从A,B两题中任选一题作答.我选择 题.
(1)、请你将小文列表、描点、连线的过程补充完整;(2)、请从A,B两题中任选一题作答.我选择 题.A.根据小文的探索过程,类比研究图象时得到的结论,写出函数图象的两个结论.
B.小文类比探索函数图象的过程,借助下面的平面直角坐标系,进一步研究函数(为常数,且)的图象.他从特殊到一般选取 , , , …等具体情况,通过列表、描点、连线等步骤,画出它们的图象,并归纳出函数图象的一般结论,请你帮他总结得到的结论.(写出任意两条即可)
23. 如图,在平面直角坐标系中,一次函数的图象分别与轴、轴交于点 , , 点是线段上的一个动点(不与点 , 点重合),过点作轴的垂线交直线于点 , 在射线上取点 , 使.设点的横坐标为.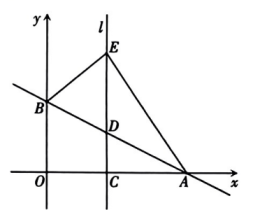 (1)、求 , 两点的坐标;(2)、若点落在直线上,求的值;(3)、请从A,B两题中任选一题作答.我选择 题.
(1)、求 , 两点的坐标;(2)、若点落在直线上,求的值;(3)、请从A,B两题中任选一题作答.我选择 题..若线段的长等于的一半时,求的值.
.若的面积等于面积的一半,求的值.