山西省新绛县2023-2024学年七年级上学期数学期中考试试卷
试卷更新日期:2023-12-25 类型:期中考试
一、选择题.(本大题共10个小题,每小题3分,共30分.将下列各题中唯一符合题意的选项字母填入题后括号内)
-
1. 下列各式符合代数式书写规则的是( )A、a×5 B、a7 C、 D、2. 用一个平面截一个几何体,得到的截面是四边形,则这个几何体可能是( ).A、球体 B、圆柱 C、圆锥 D、三棱锥3. “亚洲基础设施投资银行”是由中国提出创建的区域性金融机构,创始成员国为57个,截至2019年4月,成员总数达97个,其法定资本金为100 000 000 000美元,用科学记数法表示为( )美元.A、 B、 C、 D、4. 下列给出的数轴中正确的是( )A、
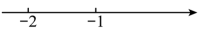 B、
B、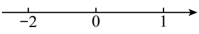 C、
C、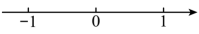 D、
D、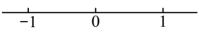 5. 下列运算正确的是( )A、 B、 C、 D、6. 在下列结论中,错误的是( )A、棱柱的侧面数与侧棱数相同 B、棱柱的棱数一定是的倍数 C、棱柱的面数一定是奇数 D、棱柱的顶点一定是偶数7. 化简(2a-b)-(2a+b)的结果为( )A、2b B、-2b C、4a D、-4a8. 下列单项式按一定规律排列: , , , , , …,其中第个单项式为( )A、 B、 C、 D、9. 若当x=2时, , 则当x=-2时,求多项式的值为( )A、-5 B、-2 C、2 D、510. 将正奇数按下表排成5列:
5. 下列运算正确的是( )A、 B、 C、 D、6. 在下列结论中,错误的是( )A、棱柱的侧面数与侧棱数相同 B、棱柱的棱数一定是的倍数 C、棱柱的面数一定是奇数 D、棱柱的顶点一定是偶数7. 化简(2a-b)-(2a+b)的结果为( )A、2b B、-2b C、4a D、-4a8. 下列单项式按一定规律排列: , , , , , …,其中第个单项式为( )A、 B、 C、 D、9. 若当x=2时, , 则当x=-2时,求多项式的值为( )A、-5 B、-2 C、2 D、510. 将正奇数按下表排成5列:第1列
第2列
第3列
第4列
第5列
第1行
1
3
5
7
第2行
15
13
11
9
第3行
17
19
21
23
…
…
…
27
25
若2023在第m行第n列,则( )
A、257 B、258 C、508 D、509二、填空题(本大题共5个小题,每小题3分,共15分)
-
11. -1.5的倒数是 .12. 面数为5的几何体可能是(只填一种就行).13. 若 , ,且 , 异号,则 .14. 观察下列“蜂窝图”,按照这样的规律,则第16个图案中的“
 ”的个数是 .
”的个数是 .  15. 要给长、宽、高分别为x , y , z的箱子打包,其打包方式如图所示,则打包带(图中粗线)的长至少为.(用含x , y , z的式子表示)
15. 要给长、宽、高分别为x , y , z的箱子打包,其打包方式如图所示,则打包带(图中粗线)的长至少为.(用含x , y , z的式子表示)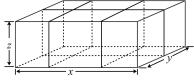
三、解答题(本大题共8个小题,共75分,解答时应写出必要的文字说明、推理过程或演算步骤)
-
16. 计算:(1)、(2)、17. 已知多项式M= .(1)、当x=1,y=2,求M的值;(2)、若多项式M与字母x的取值无关,求y的值.18. 如图,把一边长为的正方形纸板的四个角各剪去一个边长为的小正方形,然后把它折成一个无盖纸盒.
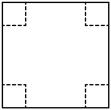 (1)、求该纸盒的表面积;(2)、若 , 时,求该纸盒的体积;(3)、为了使纸盒底面更加牢固且达到废物利用的目的,现考虑将剪下的四个小正方形平铺在盒子的底面,要求既不重叠又恰好铺满(不考虑纸板的厚度),请直接写出此时x与y之间的倍数关系.19. 自2020年“新冠肺炎”疫情暴发以来,做好个人防护的最佳措施就是出门佩戴口罩,使得医用口罩销量大增加,某口罩加工厂为满足市场需求计划每天生产10000个,但由于各种原因实际每天生产量与计划相比有出入,下表是九月份某一周的生产情况(超产为正,减产为负,单位:个).
(1)、求该纸盒的表面积;(2)、若 , 时,求该纸盒的体积;(3)、为了使纸盒底面更加牢固且达到废物利用的目的,现考虑将剪下的四个小正方形平铺在盒子的底面,要求既不重叠又恰好铺满(不考虑纸板的厚度),请直接写出此时x与y之间的倍数关系.19. 自2020年“新冠肺炎”疫情暴发以来,做好个人防护的最佳措施就是出门佩戴口罩,使得医用口罩销量大增加,某口罩加工厂为满足市场需求计划每天生产10000个,但由于各种原因实际每天生产量与计划相比有出入,下表是九月份某一周的生产情况(超产为正,减产为负,单位:个).星期
一
二
三
四
五
六
日
增减
(1)、根据记录可知前三天共生产了多少个口罩?(2)、产量最多的一天比产量最少的一天多生产多少个?(3)、该口罩加工厂实行计件工资制,每生产一个口罩0.2元,本周口罩加工厂应支付工人的工资总额是多少元?20. 由一些大小相同的小正方体组成的几何体的主视图和俯视图如图: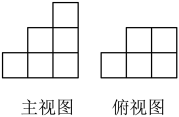 (1)、请你画出这个几何体两种可能的左视图;(2)、若组成这个几何体的小正方体的个数为n , 请你写出n的所有可能值,并简要说明你的思考过程.21. 在整数的除法运算中,只有能整除与不能整除两种情况,当不能整除时,就会产生余数,现在我们利用整数的除法运算来研究一种数——“差—数”.定义:对于一个自然数,如果这个数除以7余数是6,且除以5余数为4,则称这个数为“差一数”.例如: , , 所以34是“差一数”; , , 所以27不是“差一数”.(1)、判断69和97是否为“差—数”?并说明理由;(2)、求大于500且小于600的所有“差—数”.22. 观察下列等式:①;②;③ . 将以上三个等式两边分别相加,得 .(1)、请你写出第n个等式:;(2)、已知与互为相反数,试求:的值;(3)、探究并计算: .23. 我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”,数形结合是解决数学问题的重要思想方法,例如,代数式的几何意义是数轴上x所对应的点与2所对应的点之间的距离;因为 , 所以的几何意义就是数轴上x所对应的点与所对应的点之间的距离.
(1)、请你画出这个几何体两种可能的左视图;(2)、若组成这个几何体的小正方体的个数为n , 请你写出n的所有可能值,并简要说明你的思考过程.21. 在整数的除法运算中,只有能整除与不能整除两种情况,当不能整除时,就会产生余数,现在我们利用整数的除法运算来研究一种数——“差—数”.定义:对于一个自然数,如果这个数除以7余数是6,且除以5余数为4,则称这个数为“差一数”.例如: , , 所以34是“差一数”; , , 所以27不是“差一数”.(1)、判断69和97是否为“差—数”?并说明理由;(2)、求大于500且小于600的所有“差—数”.22. 观察下列等式:①;②;③ . 将以上三个等式两边分别相加,得 .(1)、请你写出第n个等式:;(2)、已知与互为相反数,试求:的值;(3)、探究并计算: .23. 我国著名数学家华罗庚说过“数缺形时少直观,形少数时难入微”,数形结合是解决数学问题的重要思想方法,例如,代数式的几何意义是数轴上x所对应的点与2所对应的点之间的距离;因为 , 所以的几何意义就是数轴上x所对应的点与所对应的点之间的距离.发现问题:代数式的最小值是多少?
探究问题:在数轴上,点A、B、P分别表示的是 , 2,x , 易得 .
的几何意义是线段与的长度之和,
①当点P位于点A的左侧时,如图1,这时

②当点P位于线段上(含点A、点B)时,如图2,这时 .
 (1)、问题解决:请你仿照上面的解题思路,自己画图并完成第三种情形,并写出最终的结论.(2)、拓展应用:代数式的最小值是 .(3)、当a为何值时,的最小值是2.
(1)、问题解决:请你仿照上面的解题思路,自己画图并完成第三种情形,并写出最终的结论.(2)、拓展应用:代数式的最小值是 .(3)、当a为何值时,的最小值是2.