山西省朔州市右玉县2023-2024学年九年级上学期数学期中考试试卷
试卷更新日期:2023-12-25 类型:期中考试
一、选择题(本大题共10个小题,每小题3分,共30分)在每小题列出的四个选项中,只有一项是最符合题目要求的,请将正确选项的字母标号在答题卡相应位置涂黑.
-
1. 《国家宝藏》节目立足于中华文化宝库资源,通过对文物的梳理与总结,演绎文物背后的故事与历史,让更多的观众走进博物馆,让一个个馆藏文物鲜活起来.下面四幅图是我国一些博物馆的标志,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 袋子中装有4个黑球和2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出3个球,下列事件是必然事件的是( )A、至少有一个黑球 B、至少有一个白球 C、至少有两个黑球 D、至少有两个白球3. 如图,四边形是的内接四边形, , 则的度数是( )
2. 袋子中装有4个黑球和2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出3个球,下列事件是必然事件的是( )A、至少有一个黑球 B、至少有一个白球 C、至少有两个黑球 D、至少有两个白球3. 如图,四边形是的内接四边形, , 则的度数是( )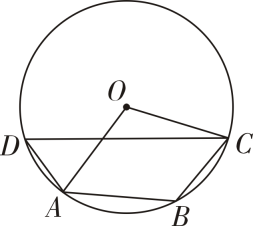 A、
A、
B、
C、
D、4. 如图所示,一圆弧过方格的格点 , 试在方格中建立平面直角坐标系,使点的坐标为 , 则该圆弧所在圆的圆心坐标是( ) A、 B、 C、 D、5. 将抛物线通过平移后,得到抛物线的解析式为 , 则平移的方向和距离是( )A、向右平移2个单位长度,再向上平移3个单位长度 B、向右平移2个单位长度,再向下平移3个单位长度 C、向左平移2个单位长度,再向上平移3个单位长度 D、向左平移2个单位长度,再向下平移3个单位长度6. 已知正多边形的一个外角为72°,则该正多边形的边数是( )A、5 B、6 C、8 D、107. “敬老爱老”是中华民族的优秀传统美德.小刚、小强计划利用暑期从 , , 三处养老服务中心中,随机选择一处参加志愿服务活动,则两人恰好选到同一处的概率是( )A、 B、 C、 D、8. 如图,是的直径,与相切于点 , , 的延长线交于点 , 则的度数是( )
A、 B、 C、 D、5. 将抛物线通过平移后,得到抛物线的解析式为 , 则平移的方向和距离是( )A、向右平移2个单位长度,再向上平移3个单位长度 B、向右平移2个单位长度,再向下平移3个单位长度 C、向左平移2个单位长度,再向上平移3个单位长度 D、向左平移2个单位长度,再向下平移3个单位长度6. 已知正多边形的一个外角为72°,则该正多边形的边数是( )A、5 B、6 C、8 D、107. “敬老爱老”是中华民族的优秀传统美德.小刚、小强计划利用暑期从 , , 三处养老服务中心中,随机选择一处参加志愿服务活动,则两人恰好选到同一处的概率是( )A、 B、 C、 D、8. 如图,是的直径,与相切于点 , , 的延长线交于点 , 则的度数是( ) A、 B、 C、 D、9. 某种商品原来每件售价为150元,经过连续两次降价后,该种商品每件售价为96元,设平均每次降价的百分率为x,根据随意,所列方程正确的是( )A、 B、 C、 D、10. 如图,四边形是的内接四边形, , . 若的半径为5,则的长为( )
A、 B、 C、 D、9. 某种商品原来每件售价为150元,经过连续两次降价后,该种商品每件售价为96元,设平均每次降价的百分率为x,根据随意,所列方程正确的是( )A、 B、 C、 D、10. 如图,四边形是的内接四边形, , . 若的半径为5,则的长为( )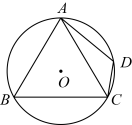 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共5个小题,每小题3分,共15分)
-
11. 若点M(a,-2),N(3,b)关于原点对称,则a+b=12. 若关于x的一元二次方程有实数根,则k的取值范围是 .13. 如图,四边形是的内接四边形,是的直径, , 则的度数是 .
 14. 如图,在正方形中,分别以四个顶点为圆心,以边长的一半为半径画圆弧,若随机向正方形内投一粒米米粒大小忽略不计 , 则米粒落在图中阴影部分的概率为 .
14. 如图,在正方形中,分别以四个顶点为圆心,以边长的一半为半径画圆弧,若随机向正方形内投一粒米米粒大小忽略不计 , 则米粒落在图中阴影部分的概率为 .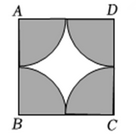 15. 《九章算术》中记载:“今有勾八步,股一十五步.问勾中容圆,径几何?”译文:现在有一个直角三角形,短直角边的长为8步,长直角边的长为15步.问这个直角三角形内切圆的直径是多少?书中给出的算法译文如下:如图,根据短直角边的长和长直角边的长,求得斜边的长.用直角三角形三条边的长相加作为除数,用两条直角边相乘的积再乘2作为被除数,计算所得的商就是这个直角三角形内切圆的直径.根据以上方法,求得该直径等于步.(注:“步”为长度单位)
15. 《九章算术》中记载:“今有勾八步,股一十五步.问勾中容圆,径几何?”译文:现在有一个直角三角形,短直角边的长为8步,长直角边的长为15步.问这个直角三角形内切圆的直径是多少?书中给出的算法译文如下:如图,根据短直角边的长和长直角边的长,求得斜边的长.用直角三角形三条边的长相加作为除数,用两条直角边相乘的积再乘2作为被除数,计算所得的商就是这个直角三角形内切圆的直径.根据以上方法,求得该直径等于步.(注:“步”为长度单位)
三、解答题(本大题共8个小题,共75分)解答应写出文字说明,证明过程或演算步骤.
-
16. 解方程:(1)、(2)、17. 我市某中学举行“中国梦·我的梦”的演讲比赛,赛后整理参赛学生的成绩,将学生的成绩分为A、B、C、D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整,请你根据统计图解答下列问题.
 (1)、参加比赛的学生人数共有名,在扇形统计图中,表示“D等级”的扇形的圆心角为度,图中m的值为;(2)、补全条形统计图;(3)、组委会决定从本次比赛获得A等级的学生中,选出两名去参加市中学生演讲比赛,已知A等级中男生只有1名,请用画树状图或列表的方法求出所选学生恰好是一男一女的概率.18. 在长度均为1的正方形网格中建立如图所示的平面直角坐标系,已知点A、B、C的坐标分别为 .
(1)、参加比赛的学生人数共有名,在扇形统计图中,表示“D等级”的扇形的圆心角为度,图中m的值为;(2)、补全条形统计图;(3)、组委会决定从本次比赛获得A等级的学生中,选出两名去参加市中学生演讲比赛,已知A等级中男生只有1名,请用画树状图或列表的方法求出所选学生恰好是一男一女的概率.18. 在长度均为1的正方形网格中建立如图所示的平面直角坐标系,已知点A、B、C的坐标分别为 . (1)、将沿着x轴向左平移5个单位后得到 , 请在图中画出平移后的;(2)、将绕着O顺时针旋转后得到 , 请在图中画出旋转后的;(3)、将线段绕着某个定点旋转后得到(其中点A的对应点为点 , 点B的对应点为点),则这个定点的坐标是 .19. 为了解我国的数学文化,小明和小红从《九章算术》《孙子算经》《海岛算经》(依次用A、B、C表示)三本书中随机抽取一本进行阅读,小明先随机抽取一本,小红再从剩下的两本中随机抽取一本.请用列表或画树状图的方法表示所有可能出现的结果.并求抽取两本书中有《九章算术》的概率.20. 日晷仪也称日晷,是观测日影记时的仪器,它是根据日影的位置,指定当时的时辰或刻数,是我国古代较为普遍使用的计时仪器,小东为了探究日晷的奥秘,在不同时刻对日晷进行了观察,如图,日晷的平面是以点O为圆心的圆,线段BC是日晷的底座,点D为日晷与底座的接触点(即与相切于点D),点在上,O为某一时刻晷针的影长,O的延长线与交于点E , 与交于点B , 连接C , , dm,.
(1)、将沿着x轴向左平移5个单位后得到 , 请在图中画出平移后的;(2)、将绕着O顺时针旋转后得到 , 请在图中画出旋转后的;(3)、将线段绕着某个定点旋转后得到(其中点A的对应点为点 , 点B的对应点为点),则这个定点的坐标是 .19. 为了解我国的数学文化,小明和小红从《九章算术》《孙子算经》《海岛算经》(依次用A、B、C表示)三本书中随机抽取一本进行阅读,小明先随机抽取一本,小红再从剩下的两本中随机抽取一本.请用列表或画树状图的方法表示所有可能出现的结果.并求抽取两本书中有《九章算术》的概率.20. 日晷仪也称日晷,是观测日影记时的仪器,它是根据日影的位置,指定当时的时辰或刻数,是我国古代较为普遍使用的计时仪器,小东为了探究日晷的奥秘,在不同时刻对日晷进行了观察,如图,日晷的平面是以点O为圆心的圆,线段BC是日晷的底座,点D为日晷与底座的接触点(即与相切于点D),点在上,O为某一时刻晷针的影长,O的延长线与交于点E , 与交于点B , 连接C , , dm,. (1)、求证:;(2)、求的长.21. 如图,是的直径,点C , D是上异侧的两点, , 交的延长线于点E , 且平分 .
(1)、求证:;(2)、求的长.21. 如图,是的直径,点C , D是上异侧的两点, , 交的延长线于点E , 且平分 . (1)、求证:是的切线.(2)、若 , , 求图中阴影部分的面积.22. 教材中有这样一道题:如图1,四边形是正方形,G是上的任意一点,于点E, , 且交于点F.求证: .
(1)、求证:是的切线.(2)、若 , , 求图中阴影部分的面积.22. 教材中有这样一道题:如图1,四边形是正方形,G是上的任意一点,于点E, , 且交于点F.求证: .
小明通过证明解决了问题,在此基础上他进一步提出了以下以下回题,请你解答.
(1)、若图1中的点G为延长线上一点,其余条件不变,如图2所示,猜想此时 , , 之间的数量关系,并证明你的结论.(2)、将图1中的绕点A逆时针旋转,使得与重合,记此时点F的对应点为点 , 如图3所示,若正方形的边长为3,求的长度.23. 在平面直角坐标系中,二次函数的图像与轴的交点为 , 两点,与轴交于点 , 顶点为 , 其对称轴与轴交于点 . (1)、求二次函数解析式;(2)、连接 , , , 试判断的形状,并说明理由;(3)、点为第三象限内抛物线上一点,的面积记为 , 求的最大值及此时点的坐标;(4)、在线段上,是否存在点 , 使为等腰三角形?若存在,直接写出点的坐标;若不存在,请说明理由.
(1)、求二次函数解析式;(2)、连接 , , , 试判断的形状,并说明理由;(3)、点为第三象限内抛物线上一点,的面积记为 , 求的最大值及此时点的坐标;(4)、在线段上,是否存在点 , 使为等腰三角形?若存在,直接写出点的坐标;若不存在,请说明理由.