山西省吕梁市交城县2023-2024学年九年级上学期数学期中考试试卷
试卷更新日期:2023-12-25 类型:期中考试
一、选择题(本大题共10个小题,每小题3分,共30分)
-
1. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、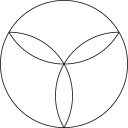 C、
C、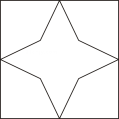 D、
D、 2. 一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根3. 如图,从正面看碗的轮廓近似一条抛物线,以顶点C为原点建立平面直角坐标系,若AB=16,CD=5,则此抛物线的解析式为( )
2. 一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根3. 如图,从正面看碗的轮廓近似一条抛物线,以顶点C为原点建立平面直角坐标系,若AB=16,CD=5,则此抛物线的解析式为( )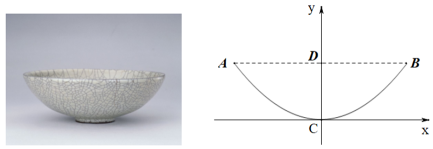 A、 B、 C、 D、4. 在足球联赛中,每两支足球队之间要进行一次主场比赛和一次客场比赛,共进行了20场比赛,请问共有多少支足球队参加了足球联赛?( )A、10 B、6 C、5 D、45. 已知A(1,2)是抛物线上的一点,点A与点B关于对称轴对称,则点B的坐标为( )A、(-2,2) B、(-4,2) C、(-5,2) D、(-5,)6. 将抛物线向左平移1个单位长度,再向下平移3个单位长度,平移后的抛物线顶点坐标为( )A、(-4,-5) B、(-2,5) C、(-5,2) D、(2,-5)7. 如图,AB是⊙O的直径,∠ABC=55°,则∠CDB的度数是( )
A、 B、 C、 D、4. 在足球联赛中,每两支足球队之间要进行一次主场比赛和一次客场比赛,共进行了20场比赛,请问共有多少支足球队参加了足球联赛?( )A、10 B、6 C、5 D、45. 已知A(1,2)是抛物线上的一点,点A与点B关于对称轴对称,则点B的坐标为( )A、(-2,2) B、(-4,2) C、(-5,2) D、(-5,)6. 将抛物线向左平移1个单位长度,再向下平移3个单位长度,平移后的抛物线顶点坐标为( )A、(-4,-5) B、(-2,5) C、(-5,2) D、(2,-5)7. 如图,AB是⊙O的直径,∠ABC=55°,则∠CDB的度数是( ) A、20° B、30° C、35° D、55°8. 某工厂生产一种产品,第一季度生产了10万件,由于市场供不应求,该工厂加大了产量,此后两个季度产量逐季度增加,前三个季度共生产36.4万件.已知第二季度和第三季度的增长率相同.设第二季度和第三季度的增长率为 , 则可列正确的方程为( )A、 B、 C、 D、9. 如图,将△ABC绕点A逆时针旋转得到△ADE,连接CE,四边形ACED是平行四边形,若∠ACB=30°,则∠AEC的度数为( )
A、20° B、30° C、35° D、55°8. 某工厂生产一种产品,第一季度生产了10万件,由于市场供不应求,该工厂加大了产量,此后两个季度产量逐季度增加,前三个季度共生产36.4万件.已知第二季度和第三季度的增长率相同.设第二季度和第三季度的增长率为 , 则可列正确的方程为( )A、 B、 C、 D、9. 如图,将△ABC绕点A逆时针旋转得到△ADE,连接CE,四边形ACED是平行四边形,若∠ACB=30°,则∠AEC的度数为( )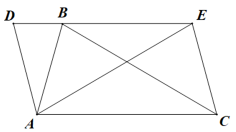 A、45° B、60° C、75° D、90°10. 如图,△ABC是直角三角形,∠ACB=90°,∠A=30°,BC=2,以AC为直径作⊙O,交AB于点D,则图中阴影部分的面积为( )
A、45° B、60° C、75° D、90°10. 如图,△ABC是直角三角形,∠ACB=90°,∠A=30°,BC=2,以AC为直径作⊙O,交AB于点D,则图中阴影部分的面积为( )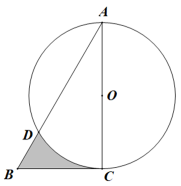 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共5个小题,每小题3分,共15分)
-
11. 把二次函数化为顶点式为.12. 如图,在平面直角坐标系中,将△ABO绕着原点O逆时针旋转90°得到△A′B′O,则点A的对应点A′的坐标为.
 13. 如图,AB是⊙O的直径,弦CD⊥AB于点E,CD=AE=8cm,则OC的长为cm.
13. 如图,AB是⊙O的直径,弦CD⊥AB于点E,CD=AE=8cm,则OC的长为cm.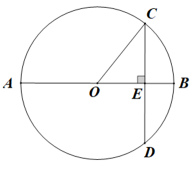 14. 已知点A , B , C三点在抛物线上,则 , , 的大小关系是为 .15. 我们约定: 为函数 的关联数,当其图象与坐标轴交点的横、纵坐标均为整数时,该交点为“整交点”,若关联数为 的函数图象与x轴有两个整交点(m为正整数),则这个函数图象上整交点的坐标为.
14. 已知点A , B , C三点在抛物线上,则 , , 的大小关系是为 .15. 我们约定: 为函数 的关联数,当其图象与坐标轴交点的横、纵坐标均为整数时,该交点为“整交点”,若关联数为 的函数图象与x轴有两个整交点(m为正整数),则这个函数图象上整交点的坐标为.三、解答题(本大题共8个小题,共75分)
-
16. 按要求解下列方程:(1)、(公式法)(2)、(因式分解法)17. 已知关于的一元二次方程.(1)、求证:该一元二次方程总有实数根;(2)、若该方程的两个根为 , , 并且 , 试求的值.18. 为了喜迎杭州第十九届亚运会,某学校计划对一块宽为20m,长为32m的矩形荒地进行改造,要求修筑同样宽鹅卵石小路,余下的部分种上草坪(阴影部分),并使草坪的面积为540㎡.现在邀请全校同学参与设计,下面是三位同学分别设计的方案,请你选择一种方案,求出道路的宽为多少米?(根据需要精确到0.1米)
 19. 一次函数的图象与二次函数的图象交于点A(4,5),B(-1,0).
19. 一次函数的图象与二次函数的图象交于点A(4,5),B(-1,0).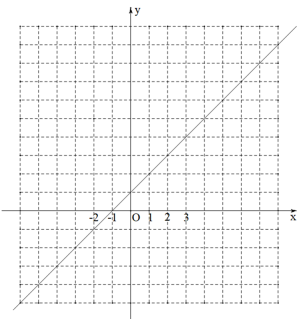 (1)、确定二次函数的表达式;(2)、请在如图所示的网格中画出二次函数的图象;(3)、根据函数的图象直接写出不等式的解集.20. 如图,AB是⊙O的直径,点C,D是AB同侧圆上两点,AC=BD,AD与BC交于点E,延长AD到F使DF=DE,连接BF.
(1)、确定二次函数的表达式;(2)、请在如图所示的网格中画出二次函数的图象;(3)、根据函数的图象直接写出不等式的解集.20. 如图,AB是⊙O的直径,点C,D是AB同侧圆上两点,AC=BD,AD与BC交于点E,延长AD到F使DF=DE,连接BF.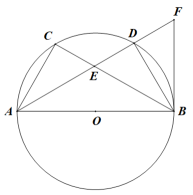 (1)、求证:CE=DE;(2)、若AD平分∠BAC,求证:BF为⊙O的切线.21. 五一商场经销一种商品,每千克成本为50元.经销售发现,该种商品每天销售量(千克)与销售单价(元/千克)满足一次函数关系,其每天销售单价、销售量满足的四组值如下:
(1)、求证:CE=DE;(2)、若AD平分∠BAC,求证:BF为⊙O的切线.21. 五一商场经销一种商品,每千克成本为50元.经销售发现,该种商品每天销售量(千克)与销售单价(元/千克)满足一次函数关系,其每天销售单价、销售量满足的四组值如下:销售单价(元/千克)
55
60
65
70
销售量(千克)
70
60
50
40
(1)、请确定与之间的函数关系式;(2)、当销售单价定为多少元时,才能使当天的销售利润最大?最大利润是多少元?22. 综合与实践
【问题情境】
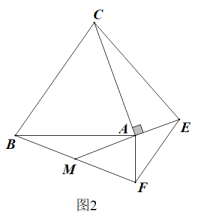
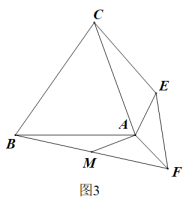
如图1,有两张等腰三角形纸片ABC和AEF,其中AB=AC,AE=AF,∠BAC+∠EAF=180°.△AEF绕着A顺时针旋转,旋转角为(),点M为BF的中点.
【特例感知】
(1)、如图1,当时,AM和CE的数量关系是;(2)、如图2,当时,连接AM,CE,请判断AM和CE的数量关系,并说明理由;(3)、【深入探究】如图3,当为任意锐角时,连接AM,CE,则(2)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.
23. 如图1,二次函数的图象交轴于点A,点B,交轴于点C,过点A的直线AD与抛物线交于点D(4,5). (1)、请确定直线AD的解析式;(2)、连接BC,点P是抛物线上的一个动点,过点P作轴的平行线交直线AD于点E,交线段BC于点F.
(1)、请确定直线AD的解析式;(2)、连接BC,点P是抛物线上的一个动点,过点P作轴的平行线交直线AD于点E,交线段BC于点F.①如果点P在第四象限的抛物线上运动,当PE=3PF时,求点P的坐标;
②设直线AD与轴的交点为G,如图2,在点P运动的过程中是否存在以点C,G,E,P为顶点的四边形为平行四边形,若存在,直接写出点P的坐标;若不存在,请说明理由.