山西省吕梁市交城县2023-2024学年七年级上学期数学期中考试试卷

试卷更新日期：2023-12-25 类型：期中考试

进入出卷网下载

一、选择题(本大题共10个小题，每小题3分，共30分)

1. 下列各数中是负数的是（）

A、0.4 B、0 C、 $\frac{1}{2}$ D、-1

查看试题解析
2. 下列说法正确的是（）

A、整数分为正整数和负整数 B、正分数和负分数统称为分数 C、有理数分为整数和小数 D、0可以是正整数也可以是负整数

查看试题解析
3. 如图，数轴上的单位长度为1，如果点A表示的数是-3，那么点B表示的数是（）

A、-1 B、0 C、2 D、3

查看试题解析
4. 下列各项中与 $5 a b_{}^{2}$ 是同类项的是（）

A、 $5 a_{}^{2} b$ B、 $4 a_{}^{2} b_{}^{2}$ C、 $- b_{}^{2} a$ D、 $5 x y_{}^{2}$

查看试题解析
5. 下列各对数中互为相反数的是（）

A、-（+2）和+（-2） B、 $| - 5 |$ 和-（-5） C、 $- | + 2 |$ 和-（-2） D、 $\frac{1}{2}$ 和2

查看试题解析
6. 下列变形中正确使用加法交换律的是（）

A、（-5）+（-8）= -（5+8） B、（-7）+11=7+（-11） C、（-3）+（-4）=（-4）+（-3） D、4+6=（-4）+（-6）

查看试题解析
7. 已知 $a = - \frac{1}{2}$ ， $| a | = | b |$ ，则 $b$ 的值是（）

A、 $\frac{1}{2}$ B、 $\pm \frac{1}{2}$ C、0 D、 $- \frac{1}{2}$

查看试题解析
8. 下列去括号正确的是（）

A、 $- 3 (x + y) = - 3 x + 3 y$ B、 $- (- a - b) = a + b$ C、 $a - 2 (b - c) = a - 2 b + c$ D、 $x - (3 y + m) = x - 3 y + m$

查看试题解析
9. 给代数式 $3 a$ 赋予实际意义，下列四个例子中错误的是（）

A、若土豆的价格是3元/ $k g$ ，则 $3 a$ 表示买 $a$ $k g$ 土豆的金额 B、若 $a$ 表示一个等边三角形的边长，则 $3 a$ 表示这个等边三角形的周长 C、若一个两位数十位上的数字为3，个位上的数字为 $a$ ，则这个两位数可表示为 $3 a$ D、某文具的进价为 $a$ 元，已知销售这种文具能盈利50%，则销售两件这种文具的销售额为 $3 a$ 元

查看试题解析
10. 已知关于 $x$ 的多项式 $m x_{}^{2} - m x - 2$ 与 $3 x_{}^{2} + m x + m$ 的和是单项式，则代数式 $m_{}^{2} - 4 m + 4$ 的值是（）

A、0 B、2或-3 C、25 D、25或0

查看试题解析

二、填空题(本大题共5个小题，每小题3分，共15分)

11. 请写出一个含字母 $a$ 的三次二项式是.

查看试题解析
12. 三峡电站是世界上装机容量最大的水电站，总装机容量为2250万千瓦.将数据2250万用科学记数法表示为．

查看试题解析
13. 比较大小： $- \frac{5}{8}$ $- \frac{7}{9}$ （填“>”或“=”或“<”）.

查看试题解析
14. 古希腊数学家把1，3，6，10，15，21，…这样的数叫做三角形数，因为它的规律性可以用下图表示.
根据图形，若把第一个图形表示的三角形数记为 $a_{1}^{} = 1$ ，第二个图形表示的三角形数记为 $a_{2}^{} = 3$ ，第三个图形表示的三角形数记为 $a_{3}^{} = 6$ ， …，则第 $n$ 个图形表示的三角形数记为 $a_{n}^{} =$ .（用含 $n$ 的式子表示）

查看试题解析
15. 如图，在数轴上点A表示的数 $a$ 是 $（ - 2 ）_{}^{3}$ 的相反数，点B表示的数 $b$ 是最小的正整数，点C表示的数 $c$ 是绝对值是3的负整数.若将数轴折叠，使得点A与点C重合，则与点B重合的点表示的数是 .

查看试题解析

三、解答题(本大题共8个小题，共75分)

16. 计算：

(1)、 $(- 5) + (- 7) - (- 4) + (- 2)$

(2)、 $(- \frac{2}{3}) \div (- 5 \frac{1}{6}) \times 6 \frac{1}{5} - 2 \frac{1}{5}$

查看试题解析
17. 计算：

(1)、 $- 1_{}^{4} + 16 \times 4 \div (- 2)_{}^{3} - (- 3)_{}^{2}$

(2)、 $(\frac{1}{2} - \frac{2}{3} + \frac{1}{6}) \times (- 12) \div | - \frac{1}{2} |$

查看试题解析
18. 化简：

(1)、 $5 a_{}^{2} + 2 a b - 4 a_{}^{2} - 3 a b$

(2)、 $2 x_{}^{2} - [3 (- \frac{5}{3} x_{}^{2} + \frac{2}{3} x y) - (x y - 3 x_{}^{2})] + 2 x y$

查看试题解析
19. 先化简，再求值： $3 （ a_{}^{2} - a b + 3 ） - 2 (3 a b - a_{}^{2} + 2) - 10$ ，其中 $| a - 1 | + (b + 2)_{}^{2} = 0$

查看试题解析
20. 学习了绝对值的概念后，我们知道一个非负数的绝对值等于它本身，负数的绝对值等于它的相反数，即当 $a \geq 0$ 时， $| a | = a$ ；当 $a < 0$ 时， $| a | = - a$ .请完成下面的问题：

(1)、因为 $3 < π$ ，所以 $3 - π < 0$ ， $| 3 - π | =$ $- (3 - π)$ =；

(2)、若有理数 $a < b$ ，则 $| a - b | =$ ；

(3)、计算： $| \frac{1}{3} - \frac{1}{2} | + | \frac{1}{4} - \frac{1}{3} | + | \frac{1}{5} - \frac{1}{4} | + ⋯ + | \frac{1}{2022} - \frac{1}{2021} | + | \frac{1}{2023} - \frac{1}{2022} |$

查看试题解析
21. 如图，长为 $a$ ，宽为 $b$ 的长方形被分割成7个部分，除两个阴影图形M，N外，其余的5个部分为形状和大小完全相同的小长方形，其中小长方形的宽为3.

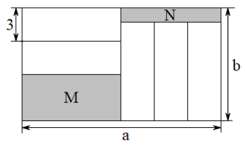(1)、求小长方形的长（用含 $a$ 的代数式表示）；

(2)、希望小组的同学们发现阴影图形M和阴影图形N的周长之和与 $a$ 的值无关，希望小组的判断是否正确，请说明理由.

查看试题解析
22. 某飞行队在广场进行特技飞行表演，若表演从空中某一高度开始，将上升的高度记为正数，下降的高度记为负数，某架飞机的五次特技飞行高度（单位：千米）记录如下表：
第一次
第二次
第三次
第四次
第五次
+2.2
-2.5
+2.8
-0.7
-0.5

(1)、求该飞机最后所在的位置比开始位置高还是低？高了或低了多少千米？

(2)、若该飞机的表演从距地面1千米的高度开始，则本次表演在进行哪次特技时距离地面最近？

(3)、如果飞机平均上升1千米需要消耗5升燃油，平均下降1千米需要消耗3升燃油，则该飞机这五次特技飞行一共消耗了多少升燃油？

查看试题解析
23. 甲、乙两家商店同时出售某种品牌的茶壶和茶杯，茶壶的单价都是每把30元，茶杯的单价每只5元．这两家商店都有优惠，甲店买一把茶壶赠送茶杯一只；乙店全场九折优惠．小明爸爸需买茶壶5把，茶杯若干只（不少于5只）．

(1)、设购买茶杯 $x$ $(x > 5)$ 只，如果在甲店购买，需付款多少元；如果在乙店购买，需付款多少元（用含 $x$ 的代数式表示并化简）；

(2)、当购买10只茶杯时，应在哪家店购买？为什么？

查看试题解析

第一次	第二次	第三次	第四次	第五次
+2.2	-2.5	+2.8	-0.7	-0.5