四川省南充市仪陇县2023-2024学年九年级上学期数学期中考试试卷

试卷更新日期：2023-12-25 类型：期中考试

进入出卷网下载

一、选择题(本大题共10个小题，每小题4分，共40分)每小题都有代号为A、B、C、D四个答案选项，其中只有一个是正确的．请根据正确选项的代号填涂答题卡对应位置，填涂正确记4分，不涂、错涂或多涂记0分．

1. 下列方程中，一定是一元二次方程的是（）

A、 $a x^{2} + b x + c = 0$ B、 $x^{2} = 1$ C、 $2 x^{2} - x = 2 x^{2}$ D、 $3 x^{2} + y - 2 = 0$

查看试题解析
2. 一元二次方程 $x^{2} - 2 x - 1 = 0$ 配方后可化为（）

A、 ${(x - 1)}^{2} = 0$ B、 ${(x - 1)}^{2} = 1$ C、 ${(x + 1)}^{2} = 2$ D、 ${(x - 1)}^{2} = 2$

查看试题解析
3. 抛物线 $y = {(1 - x)}^{2}$ 与 $y$ 轴的交点坐标为（）

A、 $(1 ， 0)$ B、 $(- 1 ， 0)$ C、 $(0 ， 1)$ D、 $(0 ， - 1)$

查看试题解析
4. 杨辉是世界上第一个排出丰富的纵横图和讨论其构成规律的数学家．他与秦九韶、李冶、朱世杰并称“宋元数学四大家”．他所著《田亩比类乘除算法》(1275年)提出了这样一个问题：“直田积(矩形面积)八百六十四步(平方步)，只云阔(宽)不及长一十二步(宽比长少一十二步)．问阔及长各几步．”若设阔为x步，则列方程可得（）

A、 $x^{2} + 12 x - 864 = 0$ B、 $x^{2} + 6 x - 864 = 0$ C、 $x^{2} - 6 x - 864 = 0$ D、 $x^{2} - 12 x - 864 = 0$

查看试题解析
5. 如图，菱形 $A B C D$ 的对角线 $A C$ 、 $B D$ 交于点O ， $A C = 2$ ， $B D = 8$ ，将 $△ B O C$ 绕着点C旋转 $180 °$ 得到 $△ B^{'} O^{'} C$ ，连接 $A B^{'}$ ，则 $A B^{'}$ 的长是（）

A、3 B、4 C、5 D、7

查看试题解析
6. 将抛物线 $y = x^{2}$ 向下平移1个单位长度，再向右平移2个单位长度后，得到抛物线的解析式为（）

A、 $y = {(x - 2)}^{2} - 1$ B、 $y = {(x + 2)}^{2} - 1$ C、 $y = {(x - 1)}^{2} + 2$ D、 $y = {(x - 1)}^{2} - 2$

查看试题解析
7. 已知 $a$ ， $b$ 是一元二次方程 $x^{2} + x - 2023 = 0$ 的两个实数根，则代数式 $a^{2} + 2 a + b$ 的值等于（）

A、2024 B、2023 C、2022 D、2021

查看试题解析
8. 如图，有一抛物线形拱桥，当拱顶离水面 $2 m$ 时，水面宽 $4 m$ ，当水面宽增加 $(2 \sqrt{7} - 4) m$ 时，则水面应下降的高度是（）

A、 $1 m$ B、 $1.5 m$ C、 $\sqrt{7} m$ D、 $(\sqrt{7} - 2) m$

查看试题解析
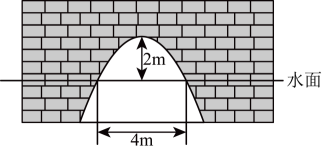9. 若关于x的方程 $m x^{2} - 3 x + 1 = 0$ 有实数根，则m的取值范围是（）

A、 $m \leq \frac{9}{4}$ 且 $m \neq 0$ B、 $m < \frac{9}{4}$ 且 $m \neq 0$ C、 $m < \frac{9}{4}$ D、 $m \leq \frac{9}{4}$

查看试题解析
10. 若关于x的方程 $2 x^{2} - 3 x + m = 2023$ 的解为 $x_{1} ， x_{2} (x_{1} < x_{2})$ ，关于x的方程 $2 x^{2} - 3 x + n = 2023$ 的解为 $x_{3} ， x_{4} (x_{3} < x_{4})$ ，且 $m < n < 0$ ．则下列结论正确的是（）

A、 $x_{1} < x_{2} < x_{3} < x_{4}$ B、 $x_{1} < x_{3} < x_{4} < x_{2}$ C、 $x_{3} < x_{1} < x_{2} < x_{4}$ D、 $x_{3} < x_{4} < x_{1} < x_{2}$

查看试题解析

二、填空题(本大题共6个小题，每小题4分，共24分)请将答案填在答题卡对应的横线上．

11. 方程 $x^{2} = x$ 的解是．

查看试题解析
12. 如果函数 $y = (m - 3) x^{| m - 1 |} - x + 2$ 是二次函数，那么 $m$ 的值为．

查看试题解析
13. 已知 $A (- 3 ， y_{1})$ ， $B (1 ， y_{2})$ 在抛物线 $y = - x^{2} - 4 x + c$ 上，则 $y_{1}$ $y_{2}$ (填“ $>$ ”“ $<$ ”或“ $=$ ”)

查看试题解析
14. 如图，四边形 $A B C D$ 中的两条对角线 $A C$ ， $B D$ 互相垂直， $A C + B D = 6$ ，当 $A C$ 长为时，四边形 $A B C D$ 的面积最大．

查看试题解析
15. 若实数x满足 $(x^{2} + 2 x)^{2} - 2 (x^{2} + 2 x) = 15$ ，则 $x^{2} + 2 x$ 的值是．

查看试题解析
16. 如图，在 $R t △ A B C$ 中， $A C = B C$ ，点D为 $A B$ 的中点， $∠ G D H = 90 °$ ， $∠ G D H$ 绕点D旋转， $D G 、 D H$ 分别与边 $A C ， B C$ 交于E、F两点．下列结论：① $A E = C F$ ， ② $E F = \frac{1}{2} A B$ ， ③ $S_{四边形 C E D F} = \frac{1}{3} S_{Δ A B C}$ ， ④ $A E + B F = \frac{\sqrt{2}}{2} A B$ ， ⑤ $△ D E F$ 始终为等腰直角三角形．其中正确的结论有.(填写序号)

查看试题解析

三、解答题(本大题共9个小题，共86分)解答应写出必要的文字说明、证明过程或演算步骤

17. 解方程：

(1)、 $- x^{2} - x + 1 = 0$ ；

(2)、 ${(2 x + 3)}^{2} = {(3 x - 2)}^{2}$ ．

查看试题解析
18. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，将 $△ A B C$ 绕着点 $B$ 逆时针旋转得到 $△ F B E$ ，点 $C$ ， $A$ 的对应点分别为 $E$ ， $F$ ，点 $E$ 落在 $B A$ 上，连接 $A F$ ．

(1)、若 $∠ B A C = 36 °$ ，求 $∠ B A F$ 的度数；

(2)、若 $A C = 4$ ， $B C = 3$ ，求 $A F$ 的长．

查看试题解析
19. 如图，某中学要在教学楼后面的空地上用20米长的竹篱笆围出一个矩形地块作生物园，矩形的一边用教学楼的外墙(外墙足够长)，其余三边用竹篱笆．设矩形的边 $A B$ 的长为x米，矩形 $A B C D$ 面积为y平方米．

(1)、求y与x的函数关系式，并求自变量x的取值范围；

(2)、生物园的面积能否达到55平方米？请说明理由．

查看试题解析
20. 已知关于x的一元二次方程 $x^{2} - 2 k x + 1 = 0$ ，且 $k < - 1$ ．

(1)、求证：方程总有两个不相等的实数根；

(2)、若方程的两个实数根 $x_{1} ， x_{2}$ ，满足 $x_{1} - x_{2} = k$ ，求k的值．

查看试题解析
21. 阅读思考，并解答下列问题：
在2022年北京冬季奥林匹克运动会上，一个滑雪者从山坡滑下，为了得出滑行距离s（单位： $m$ ）与滑行时间t（单位： $s$ ）之间的关系式，测得一组数据(如下表)．
滑行时间 $t / s$
0
1
2
3
4
滑行距离 $s / m$
0
$4.5$
14
$28.5$
48

(1)、为观察s与t之间的关系，建立坐标系，以t为横坐标，s为纵坐标．如图，请描出表中数据对应的5个点，并用平滑的曲线连接它们；

(2)、观察图象，可以看出这条曲线像是我们学过的哪种函数的图象的一部分？请你推测滑行距离与滑行时间的关系，并用该函数模型来近似地表示s与t之间的关系；

(3)、如果该滑雪者滑行了 $270 m$ ，请你用（2）中的函数模型推测他滑行的时间是多少秒？（参考数据： $10 4^{2} = 10816$ ）

查看试题解析
22. 配方法是数学中重要的一种思想方法，利用配方法可求一元二次方程的根，也可以求二次函数的顶点坐标等，所谓配方法是指将一个式子的某部分通过恒等变形化为完全平方式或几个完全平方式的和的方法，其实这种方法还经常被用到代数式的变形中，并结合非负数的意义解决某些问题．我们规定：一个整数能表示成 $a^{2} + b^{2}$ (a ， b是整数)的形式，则称这个数为“完美数”．例如，5是“完美数”，理由：因为 $5 = 2^{2} + 1^{2}$ ，所以5是“完美数”．

(1)、【解决问题】：
下列各数中，“完美数”有 (只填序号)；
①10 ②24 ③34 ④60

(2)、【探究问题】：
若 $y = x^{2} - 4 x + 13$ 可配方成 $y = (x - m)^{2} + n^{2}$ (m ， n为常数)，则 $m n$ 的值为；

(3)、已知 $S = a^{2} + 4 a b + 5 b^{2} - 2 b + k$ (a ， b是整数，k是常数)，要使S为“完美数”，试求出符合条件的一个k值，并说明理由；

(4)、【拓展应用】：
已知实数x ， y均满足 $x - y^{2} = 3$ ，求代数式 $x^{2} + 2 y^{2} - 4 x + 2032$ 的最小值．

查看试题解析
23. 某水果商场经销一种高档水果，原价每千克80元，若每千克盈利10元，则每天可售出400千克．经市场调查发现，在进货价不变的情况下，商场决定采取适当的涨价措施，若每千克涨价 $0.5$ 元，日销售量将减少10千克．

(1)、在原价的基础上，连续两次降价后每千克 $51.2$ 元，若每次下降的百分率相同，求每次下降的百分率；

(2)、现该商场要保证每天盈利 $4480$ 元，且要尽快减少库存，那么每千克应涨价多少元？

(3)、若使商场每天的盈利达到最大，则应涨价多少元？此时每天的最大盈利是多少？

查看试题解析
24. 探究式学习是新课程倡导的重要学习方式，某兴趣小组拟做以下探究．
如下图，将两个完全相同的三角形纸片 $△ A B C$ 和 $△ D E C$ 重合放置，其中 $∠ C = 90 °$ ．若固定 $△ A B C$ ，将 $△ D E C$ 绕点C旋转．


(1)、当 $△ D E C$ 绕点C旋转到点D恰好落在 $A B$ 边上时，如下图．

①当 $∠ B = ∠ E = 40 °$ 时，求此时旋转角的大小；
②当 $∠ B = ∠ E = α$ 时，直接写出此时旋转角的大小(用含α的式子表示)．

(2)、当 $△ D E C$ 绕点C旋转到如下图所示的位置时，小组长猜想： $△ B D C$ 的面积与 $△ A E C$ 的面积相等，试判断小组长的猜想是否正确，若正确，请你证明小组长的猜想．若不正确，请说明理由．


查看试题解析
25. 如图，已知抛物线 $y = a x^{2} + b x + 3 \sqrt{3}$ 交x轴于 $A (- 3 ， 0) ， B (9 ， 0)$ 两点，交y轴于点C ，点P是抛物线上一动点，连接 $A C ， B C$ ．

(1)、求抛物线的解析式；

(2)、在抛物线的对称轴上是否存在点Q ，使 $| B Q - C Q |$ 最大？若存在，求出点Q的坐标；若不存在，请说明理由；

(3)、连接 $C P ， B P$ ，若 $S_{△ B C P} = \frac{9}{4} S_{△ A O C}$ ，求点P的坐标．

查看试题解析

滑行时间 $t / s$	0	1	2	3	4
滑行距离 $s / m$	0	$4.5$	14	$28.5$	48

四川省南充市仪陇县2023-2024学年九年级上学期数学期中考试试卷

一、选择题(本大题共10个小题，每小题4分，共40分)每小题都有代号为A、B、C、D四个答案选项，其中只有一个是正确的．请根据正确选项的代号填涂答题卡对应位置，填涂正确记4分，不涂、错涂或多涂记0分．

二、 填空题(本大题共6个小题，每小题4分，共24分)请将答案填在答题卡对应的横线上．

三、 解答题(本大题共9个小题，共86分)解答应写出必要的文字说明、证明过程或演算步骤

二、填空题(本大题共6个小题，每小题4分，共24分)请将答案填在答题卡对应的横线上．

三、解答题(本大题共9个小题，共86分)解答应写出必要的文字说明、证明过程或演算步骤