四川省绵阳市游仙区2023-2024学年九年级上学期数学月考考试试卷(10月)
试卷更新日期:2023-12-25 类型:月考试卷
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 方程化为一元二次方程的一般形式后,二次项系数、一次项系数、常数项分别是( )A、 , , B、 , , C、 , , D、 , ,2. 二次函数的图象与轴的交点个数是( )A、个 B、个 C、个 D、不能确定3. 用配方法解方程x2+8x+7=0,则配方正确的是( )
A、(x+4)2=9 B、(x-4)2=9 C、(x-8)2=16 D、(x+8)2=574. 方程的一般式为时,的值为( )A、 B、 C、 D、5. 关于的一元二次方程的根的情况是( )A、没有实数根 B、有两个不相等的实数根
C、有两个相等的实数根 D、无法确定6. 抛物线的顶点坐标是( )A、 , B、 C、 D、7. 飞机着陆后滑行的距离单位:与滑行的时间单位:的函数解析式是 , 那么飞机着陆后滑行多长时间才能停下来( )A、 B、 C、 D、8. 将抛物线的图象先向右平移个单位,再向上平移个单位,得到的抛物线的解析式是( )A、 B、
C、 D、9. 二次函数若 , 则自变量的取值范围是( )A、或 B、或 C、 D、10. 若函数的图象与轴只有一个交点,则的值是( )A、或 B、 C、 D、11. 如图,在平面直角坐标系中,抛物线经过点 , 对称轴为直线若 , 则的取值范围是( ) A、 B、 C、 D、或12. 云南省是我国花卉产业大省,一年四季都有大量鲜花销往全国各地,花卉产业已成为该省许多地区经济发展的重要项目.近年来某乡的花卉产值不断增加, 2020年花卉产值是1000万元, 2022年花卉产值达到1400万元.设2021和2022年花卉产值的年平均增长率均为x,则下列方程正确的是( )A、1000(1+x)=1400 B、1000(1+2x)=1400 C、1000(1+x)2=1400 D、1000(1+x)+1000(1+x)2=1400
A、 B、 C、 D、或12. 云南省是我国花卉产业大省,一年四季都有大量鲜花销往全国各地,花卉产业已成为该省许多地区经济发展的重要项目.近年来某乡的花卉产值不断增加, 2020年花卉产值是1000万元, 2022年花卉产值达到1400万元.设2021和2022年花卉产值的年平均增长率均为x,则下列方程正确的是( )A、1000(1+x)=1400 B、1000(1+2x)=1400 C、1000(1+x)2=1400 D、1000(1+x)+1000(1+x)2=1400二、填空题(本大题共6小题,共24.0分)
-
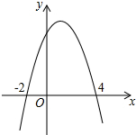
13. 方程的二次项系数、一次项系数、常数项的和为 .14. 关于的一元二次方程有一根为 , 则 .15. 已知关于的一元二次方程无实数根,则一次函数的图形不经过第 象限.16. 在一次足球邀请赛中,参赛的每两个队之间都要比赛一场,共比赛28场,设共有个队参赛,根据题意,可列方程为 .17. 已知函数是二次函数,则 .18. 如图,二次函数的图象与轴相交于和两点,当函数值时,自变量的取值范围是 .
三、解答题(本大题共9小题,共90.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 解方程:(1)、;(2)、 .20. 已知是方程的一个根,求代数式的值.21. 随着“共享经济”的概念迅速普及,共享汽车也进入了人们的视野,某共享汽车租赁公司年初在某地投放了一批共享汽车,全天包车的租金定为每辆元据统计,三月份的全天包车数为次,在租金不变的基础上,四、五月的全天包车数持续走高,五月份的全天包车数达到次.(1)、若从三月份到五月份的全天包车数月平均增长率不变,求全天包车数的月平均增长率;
(2)、从六月份起,该公司决定降低租金,尽可能地让利顾客,经调查发现,租金每降价元,全天包车数增加次,当租金降价多少元时,公司将获利元?22. 已知关于的方程 .(1)、取什么值时,方程有两个实数根;
(2)、如果方程有两个实数根 , , 且 , 求的值.23. 已知抛物线经过点和点 , 求该抛物线的解析式.24. 已知二次函数的函数值和自变量的部分对应取值如下表所示:(1)、当时.
求这个二次函数的解析式;
当抛物线下降时,求的取值范围;(2)、如果、、这三个实数中,只有一个是正数,求的取值范围.25. 如图,抛物线与轴交于点 , , 与轴交于点 , 点的坐标为 , 点的坐标为 . (1)、求抛物线的表达式;(2)、当时,抛物线有最小值 , 求的值.26. 网络销售已经成为一种热门的销售方式,为了减少农产品的库存,某市市长亲自在网络平台上进行直播销售板栗,为提高大家购买的积极性,直播时,板栗公司每天拿出元现金,作为红包发给购买者已知该板栗的成本价格为元 , 每日销售量与销售单价元满足关系式:经销售发现,销售单价不低于成本价且不高于元设板栗公司销售该板栗的日获利为元 .(1)、请求出日获利与销售单价之间的函数关系式;(2)、当销售单价定为多少时,销售这种板栗日获利最大?最大利润为多少元?27. 如图,已知正比例函数的图象与抛物线相交于点 .
(1)、求抛物线的表达式;(2)、当时,抛物线有最小值 , 求的值.26. 网络销售已经成为一种热门的销售方式,为了减少农产品的库存,某市市长亲自在网络平台上进行直播销售板栗,为提高大家购买的积极性,直播时,板栗公司每天拿出元现金,作为红包发给购买者已知该板栗的成本价格为元 , 每日销售量与销售单价元满足关系式:经销售发现,销售单价不低于成本价且不高于元设板栗公司销售该板栗的日获利为元 .(1)、请求出日获利与销售单价之间的函数关系式;(2)、当销售单价定为多少时,销售这种板栗日获利最大?最大利润为多少元?27. 如图,已知正比例函数的图象与抛物线相交于点 .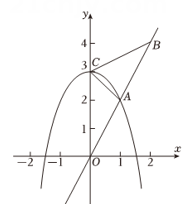 (1)、求与的值;(2)、若点在函数的图象上,抛物线的顶点是 , 求的面积;(3)、若点是轴上一个动点,求当最小时点的坐标.
(1)、求与的值;(2)、若点在函数的图象上,抛物线的顶点是 , 求的面积;(3)、若点是轴上一个动点,求当最小时点的坐标.