四川省达州市渠县2023-2024学年八年级上学期数学月考考试试卷（9月）

试卷更新日期：2023-12-25 类型：月考试卷

进入出卷网下载

一、选择题（共10小题，每小题4分，满分40分）

1. 在实数3.14， $\frac{4}{5} π$ ， $\frac{1}{2}$ ， $|- 3|$ ， $- \sqrt{3}$ ，0.33333......， 1.2323323332 ......（每相邻的两个2之间多一个3）中，无理数的个数为（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 直角三角形的最长边的长为13，一条直角边长为5，另一条直角边长为（）

A、12 B、10 C、8 D、6

查看试题解析
3. 如图字母B所代表的正方形的面积是（）

A、12 B、13 C、144 D、194

查看试题解析
4. 9的算术平方根是( )

A、3 B、±3 C、 $\sqrt{3}$ D、± $\sqrt{3}$

查看试题解析
5. 四根小棒的长分别是5，9，12，13，从中选择三根小棒首尾相接，搭成边长如下的四个三角形，其中是直角三角形的是(　　)

A、5，9，12 B、5，12，13 C、5，9，13 D、9，12，13

查看试题解析
6. 如图有一块菜地，经人工测得菜地的四周分别为AB=13，BC=3，CD=4，AD=12，∠C=90°，则这块菜地的面积为（）

A、24 B、30 C、32 D、36

查看试题解析
7. 如图，在Rt△OAB中，∠OAB＝90°，OA＝AB，边OA在数轴上．点A表示的数为1，以O为圆心，OA的长为半径画弧交数轴负半轴于点C，则C表示的数是(　　)

A、 $- \frac{3}{2}$ B、 $- \frac{5}{3}$ C、1 $- \sqrt{2}$ D、 $- \sqrt{2}$

查看试题解析
8. 如果梯子的底端离建筑物1.5米，2.5米长的梯子可以达到建筑物的高度是（）

A、2米 B、2.5米 C、3米 D、3. 5米

查看试题解析
9. 如图，图中小正方形的边长都为1，△ABC的顶点都在格点上，则△ABC是（）

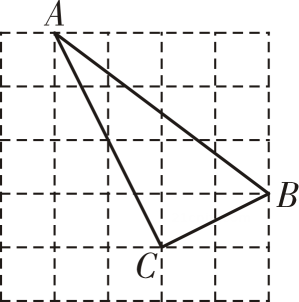A、直角三角形 B、锐角三角形 C、钝角三角形 D、无法判断

查看试题解析
10. 若3－ $\sqrt{2}$ 的整数部分为x ，小数部分为y ，则 $x - y$ 的值是(　　)

A、 $1 - \sqrt{2}$ B、 $\sqrt{2} - 1$ C、 $2 - \sqrt{2}$ D、 $\sqrt{2} - 2$

查看试题解析

二、填空题（每小题4分，共20分）

11. 如果一个直角三角形的两条直角边的长分别为3和4，则斜边上的高的长度为．

查看试题解析
12. 若一个正数的两个平方根分别是 $2 a - 1$ 和 $a + 4$ ，则 $a$ 的值是。

查看试题解析
13. 已知，如图，一轮船从港口A出发向东北方向航行了50海里，另一轮船同时从港口A出发向东南方向航行120海里，此时则两船相距海里 .

查看试题解析
14. 如果直角三角形的三条边分别为3、5、 $a$ ，那么 $a^{2}$ 的值等于

查看试题解析
15. 等腰三角形的周长是16cm，底边长是6cm，则它的面积是 $c m_{}^{2}$

查看试题解析

三、解答题（共90分）

16. 计算：

(1)、计算： $\sqrt{64} - \sqrt{144}$ ；

(2)、 ${(\sqrt{3})}^{2} - \sqrt{36} + \sqrt{{(- 2)}^{2}}$

查看试题解析
17. 有一块四边形的土地，量得各边的长分别为：AB=130米，BC=120米，CD=40米，AD=30米，∠D=90°. 求这块土地是面积是多少平方米？

查看试题解析
18. 一个正数 $x$ 的平方根分别是 $3 a ＋ 13 与 a - 5$ ，求 $a$ 和 $x$ 的值．

查看试题解析
19. 若△ABC中，∠C=90°．

(1)、若 $a = 5 ， b = 12$ ，求 $c$ ；

(2)、若 $a = 6 ， c = 10 ，$ 求 $b$ ；

查看试题解析
20. 如图，A、B两个村在河流CD的同侧，分别到河的距离为AC=10千米，BD=30千米，且CD=30千米，现在要在河边建一自来水厂，向A、B俩村供水，铺设水管的费用为每千米1万，请你在河流CD上选择水厂的位置P，使铺设水管的费用最节省，并求出总费用是多少？

查看试题解析
21. 已知 $\sqrt{a - 25}$ +3 $\sqrt{25 - a} = b - 24$ .

(1)、求 $a 、 b$ 的值；

(2)、求 $a^{2} - b^{2}$ 的平方根

查看试题解析
22. 如果a、b、c满足 $\sqrt{a - 2} + |2 b + 6| + {(c - 4)}^{2} = 0$ ，求代数式 ${(a + b + c)}^{2} - {(a - b - c)}^{2}$ 的值

查看试题解析
23. 在直角三角形△ABC中，∠ACB=90°，BC=6，AC=8. 点D是BC上一点，将△CD沿着AD折叠，使点C与定E重合。求△BDE的周长 .

查看试题解析
24. 如图，圆柱的高为6cm，底面圆的周长为12cm，在圆柱底部的A处，有一只蚂蚁，A点的对侧，圆柱内部的B处，有一小块实物，蚂蚁咬吃到B处的食物，它咬爬过的最短路程为多少cm？

查看试题解析
25. 如图，在Rt△ABC中，AC=28，BC=21，一个动点P从点A出发，以每秒1个单位的速度向点C运动，同时另一个动点Q从点B出发，以每秒2个单位的速度向点A运动，当一个点运动到达终点时另一个点也随之停止运动，运动时间为ts.

(1)、用含t的代数式表示线段AQ和CP；

(2)、t为何值时，AP=AQ?

(3)、在动点P，Q的运动过程中，判断AP与BP能否相等，并说明理由.

查看试题解析

四川省达州市渠县2023-2024学年八年级上学期数学月考考试试卷（9月）

一、 选择题（共10小题，每小题4分，满分40分）

二、填空题（每小题4分，共20分）

三、解答题（共90分）

一、选择题（共10小题，每小题4分，满分40分）