北京市四十四中2023-2024学年八年级八年级上学期数学期中考试试卷
试卷更新日期:2023-12-25 类型:期中考试
一、选择题(本题共16分,每小题2分)
-
1. 下列四个图形中,线段AD是△ABC中BC边上的高的是( )A、
 B、
B、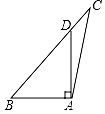 C、
C、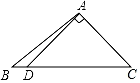 D、
D、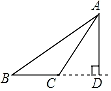 2. 用下列长度的三条线段能组成三角形的是( )A、2cm , 3cm , 5cm B、3cm , 3cm , 5cm C、5cm , 10cm , 4cm D、8cm , 12cm , 2cm3. 下列运算结果正确的是( )A、(a2)3=a6 B、a3•a4=a12 C、m3•m2•m=m5 D、(3a)3=9a34. 点M(3,﹣4)关于x轴的对称点M′的坐标是( )A、(3,4) B、(﹣3,﹣4) C、(﹣3,4) D、(﹣4,3)5. 若如图中的两个三角形全等,图中的字母表示三角形的边长,则∠1的度数为( )
2. 用下列长度的三条线段能组成三角形的是( )A、2cm , 3cm , 5cm B、3cm , 3cm , 5cm C、5cm , 10cm , 4cm D、8cm , 12cm , 2cm3. 下列运算结果正确的是( )A、(a2)3=a6 B、a3•a4=a12 C、m3•m2•m=m5 D、(3a)3=9a34. 点M(3,﹣4)关于x轴的对称点M′的坐标是( )A、(3,4) B、(﹣3,﹣4) C、(﹣3,4) D、(﹣4,3)5. 若如图中的两个三角形全等,图中的字母表示三角形的边长,则∠1的度数为( ) A、40° B、50° C、60° D、70°6. 等腰三角形的一个内角是70°,则它顶角的度数是( )A、 B、 或 C、 或 D、7. 如图,在△ABC中,BC的垂直平分线分别交AC , BC于点D , E . 若△ABC的周长为22,BE=4,则△ABD的周长为( )
A、40° B、50° C、60° D、70°6. 等腰三角形的一个内角是70°,则它顶角的度数是( )A、 B、 或 C、 或 D、7. 如图,在△ABC中,BC的垂直平分线分别交AC , BC于点D , E . 若△ABC的周长为22,BE=4,则△ABD的周长为( )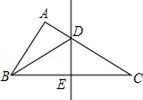 A、14 B、18 C、20 D、268. 如图,△ABC中,∠ABC、∠EAC的角平分线PA、PB交于点P , 下列结论:①PC平分∠ACF;②∠ABC+∠APC=180°;③若PM⊥BE于点M , PN⊥BF于点N , 则AM+CN=AC;④∠BAC=2∠BPC . 其中正确的是( )
A、14 B、18 C、20 D、268. 如图,△ABC中,∠ABC、∠EAC的角平分线PA、PB交于点P , 下列结论:①PC平分∠ACF;②∠ABC+∠APC=180°;③若PM⊥BE于点M , PN⊥BF于点N , 则AM+CN=AC;④∠BAC=2∠BPC . 其中正确的是( ) A、只有①②③ B、只有①③④ C、只有②③④ D、只有①③
A、只有①②③ B、只有①③④ C、只有②③④ D、只有①③二、填空题(本题共16分,每小题2分)
-
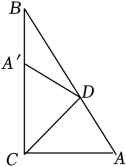
9. 在△ABC中,∠C=90°,∠A-∠B=30°,则∠A= .10. 一个多边形的内角和是720°,这个多边形的边数是 .11. 如图,Rt△ABC中,∠ACB=90°,∠A=58°,将∠A折叠,使点A落在边CB上A'处,折痕为CD , 则∠A'DB= .
 12. 如图,∠ABC=∠DCB , 请补充一个条件: , 使△ABC≌△DCB .
12. 如图,∠ABC=∠DCB , 请补充一个条件: , 使△ABC≌△DCB .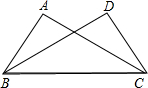 13. 已知a-2b=10,ab=5,则a2+4b2的值是 .14. 已知x2-8x+k是一个完全平方式,则常数k的值是 .15. 如图,已知∠ABC=60°,DB=24,DE=DF , 若EF=4,则BE= .
13. 已知a-2b=10,ab=5,则a2+4b2的值是 .14. 已知x2-8x+k是一个完全平方式,则常数k的值是 .15. 如图,已知∠ABC=60°,DB=24,DE=DF , 若EF=4,则BE= . 16. 如图,已知∠MON , 在边ON 上顺次取点P1 , P3 , P5…,在边OM 上顺次取点P2 , P4 , P6…,使得OP1=P1P2=P2P3=P3P4=P4P5…,得到等腰△OP1P2 , △P1P2P3 , △P2P3P4 , △P3P4P5…
16. 如图,已知∠MON , 在边ON 上顺次取点P1 , P3 , P5…,在边OM 上顺次取点P2 , P4 , P6…,使得OP1=P1P2=P2P3=P3P4=P4P5…,得到等腰△OP1P2 , △P1P2P3 , △P2P3P4 , △P3P4P5…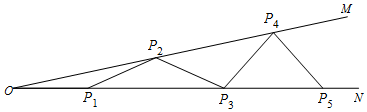 (1)、若∠MON=30°,可以得到的最后一个等腰三角形是;(2)、若按照上述方式操作,得到的最后一个等腰三角形是△P3P4P5 , 则∠MON 的度数α 的取值范围是 .
(1)、若∠MON=30°,可以得到的最后一个等腰三角形是;(2)、若按照上述方式操作,得到的最后一个等腰三角形是△P3P4P5 , 则∠MON 的度数α 的取值范围是 .三、解答题(本大题9小题共68分,17题20分,18题6分,19题4分,20题6分,21题5分,22、23、25题各7分,24题6分)
-
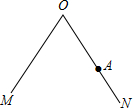
17. 计算:(1)、(a2)3•a5;(2)、2x•(x+2y);(3)、(3x+1)(3x-1);(4)、(2m-n)2;(5)、(x+2y)(5-3x);(6)、(y+2)(y-2)-(y-1)(y+5).18. 化简求值:已知a2-2a=5,求代数式(a-2)2-2(a+1)+4a的值.19. 如图,∠MON及ON上一点A .
求作:点P , 使得PA⊥ON , 且点P到∠MON两边的距离相等.
作法:
 20. 如图,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别是A(2,3),B(1,0),C(1,2).
20. 如图,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别是A(2,3),B(1,0),C(1,2).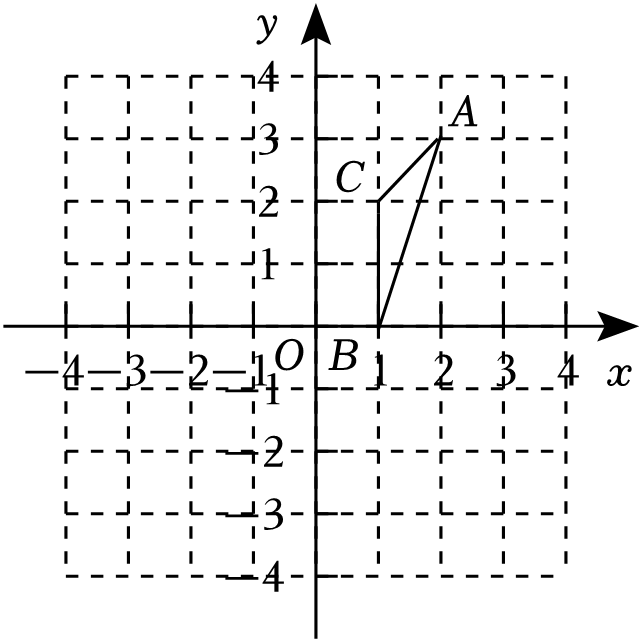 (1)、在图中作出△ABC关于y轴对称的△A1B1C1;(2)、写出点A关于x轴的对称点的坐标 ;(3)、△ABC的面积为 ;(4)、如果要使以B、C、D为顶点的三角形与△ABC全等,写出所有符合条件的点D(不与点A重合)坐标.21. 已知:如图,点A、E、F、C在同一条直线上,DF=BE,∠B=∠D,AD∥BC,求证:AE=CF.
(1)、在图中作出△ABC关于y轴对称的△A1B1C1;(2)、写出点A关于x轴的对称点的坐标 ;(3)、△ABC的面积为 ;(4)、如果要使以B、C、D为顶点的三角形与△ABC全等,写出所有符合条件的点D(不与点A重合)坐标.21. 已知:如图,点A、E、F、C在同一条直线上,DF=BE,∠B=∠D,AD∥BC,求证:AE=CF.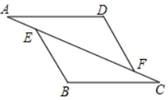 22. 如图,AB⊥AC , AB=AC , 过点B , C分别向射线AD作垂线,垂足分别为E , F .
22. 如图,AB⊥AC , AB=AC , 过点B , C分别向射线AD作垂线,垂足分别为E , F . (1)、依题意补全图形;(2)、求证:BE=EF+FC .23. 如图,CB=CD , ∠D+∠ABC=180°,CE⊥AD于E .
(1)、依题意补全图形;(2)、求证:BE=EF+FC .23. 如图,CB=CD , ∠D+∠ABC=180°,CE⊥AD于E . (1)、求证:AC平分∠DAB;(2)、若AE=10,DE=4,求AB的长.24. 我们在学习《从面积到乘法公式》时,曾用两种不同的方法计算同一个图形的面积,探索了单项式乘多项式的运算法则:m(a+b+c)=ma+mb+mc(如图1),多项式乘多项式的运算法则:(a+b)(c+d)=ac+ad+bc+bd(如图2),以及完全平方公式:(a+b)2=a2+2ab+b2(如图3).
(1)、求证:AC平分∠DAB;(2)、若AE=10,DE=4,求AB的长.24. 我们在学习《从面积到乘法公式》时,曾用两种不同的方法计算同一个图形的面积,探索了单项式乘多项式的运算法则:m(a+b+c)=ma+mb+mc(如图1),多项式乘多项式的运算法则:(a+b)(c+d)=ac+ad+bc+bd(如图2),以及完全平方公式:(a+b)2=a2+2ab+b2(如图3).把几个图形拼成一个新的图形,通过图形面积的计算,常常可以得到一些等式,这是研究数学问题的一种常用方法.
 (1)、请设计一个图形说明等式(a+b)(2a+b)=2a2+3ab+b2成立(画出示意图,并标上字母)(2)、如图4,它是由四个形状、大小完全相同的直角三角形与中间的小正方形EFGH拼成的一个大正方形ABCD . 如果每个直角三角形的较短的边长为a , 较长的边长为b , 最长的边长为c , 试用两种不同的方法计算这个大正方形的面积,你能发现直角三角形的三边长a、b、c的什么数量关系?(注:写出解答过程)25. 在△ABC中,∠C=90°,AC>BC , D是AB的中点.E为直线AC上一动点,连接DE . 过点D作DF⊥DE , 交直线BC于点F , 连接EF .
(1)、请设计一个图形说明等式(a+b)(2a+b)=2a2+3ab+b2成立(画出示意图,并标上字母)(2)、如图4,它是由四个形状、大小完全相同的直角三角形与中间的小正方形EFGH拼成的一个大正方形ABCD . 如果每个直角三角形的较短的边长为a , 较长的边长为b , 最长的边长为c , 试用两种不同的方法计算这个大正方形的面积,你能发现直角三角形的三边长a、b、c的什么数量关系?(注:写出解答过程)25. 在△ABC中,∠C=90°,AC>BC , D是AB的中点.E为直线AC上一动点,连接DE . 过点D作DF⊥DE , 交直线BC于点F , 连接EF . (1)、如图1,当E是线段AC上一点时,请依题意补全图形,并判断以AE、BF、EF三条线段为边构成的三角形是 三角形;(2)、当点E在线段CA的延长线上时,请依题意补全图2,并判断(1)中的结论是否仍成立,如果成立,请说明理由.26. 已知:在△ABC中,∠CAB=2α,且0°<α<30°,AP平分∠CAB .
(1)、如图1,当E是线段AC上一点时,请依题意补全图形,并判断以AE、BF、EF三条线段为边构成的三角形是 三角形;(2)、当点E在线段CA的延长线上时,请依题意补全图2,并判断(1)中的结论是否仍成立,如果成立,请说明理由.26. 已知:在△ABC中,∠CAB=2α,且0°<α<30°,AP平分∠CAB .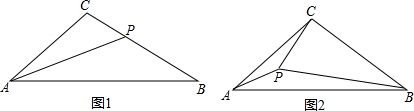 (1)、如图1,若α=21°∠ABC=32°,且AP交BC于点P , 试探究线段AB , AC与PB之间的数量关系,并对你的结论加以证明;(2)、如图2,若∠ABC=60°-α,点P在△ABC的内部,且使∠CBP=30°,求∠APC的度数(用含α的代数式表示).
(1)、如图1,若α=21°∠ABC=32°,且AP交BC于点P , 试探究线段AB , AC与PB之间的数量关系,并对你的结论加以证明;(2)、如图2,若∠ABC=60°-α,点P在△ABC的内部,且使∠CBP=30°,求∠APC的度数(用含α的代数式表示).