四川省眉山市青神县 2023-2024学年九年级上学期11月期中数学试题
试卷更新日期:2023-12-25 类型:期中考试
一、选择题:本大题共12个小题,每小题4分,共48分.
-
1. 下列二次根式属于最简二次根式的是( )A、 B、 C、 D、2. 要使二次根式 有意义,则x应满足( )A、x≠1 B、x≥1 C、x≤1 D、x<13. 一元二次方程的二次项系数、一次项系数、常数项分别是( )A、 B、 C、 D、4. 已知a:b=2:3,那么下列等式中成立的是( )A、3a=2b B、2a=3b C、 D、5. 下列各组数中互为相反数的是( )A、–2与 B、–2与 C、2与(–)2 D、|–|与6. 将一元二次方程2x2+8x+13=0通过配方转换成(x+n)2=p的形式(n,p为常数),则np的值为( )A、3 B、5 C、-5 D、-97. 若两个相似多边形的面积之比为1:4,则它们的周长之比为( )A、1:4 B、1:2 C、2:1 D、4:18. 一个等腰三角形的边长是6,腰长是一元二次方程x2-7x+12=0的一根,则此三角形的周长是( )A、12 B、12 或13 C、14 D、12或149. 为解决群众看病贵的问题,有关部门决定降低药价,对某种原价为300元的药品进行连续两次降价后为243元,设平均每次降价的百分率为x,则下面所列方程正确的是(A、300(1﹣x)2=243 B、243(1﹣x)2=300 C、300(1﹣2x)=243 D、243(1﹣2x)=30010. 如图 , 则下列式子中不成立的是( )
 A、 B、 C、 D、11. 如图,在梯形中, , , 对角线与相交于点 , 把、、、的面积分别记作、、、 , 那么下列结论中,不正确( ).
A、 B、 C、 D、11. 如图,在梯形中, , , 对角线与相交于点 , 把、、、的面积分别记作、、、 , 那么下列结论中,不正确( ). A、 B、 C、 D、12. 如图,在钝角三角形中,分别以和为斜边向的外侧作等腰直角三角形和等腰直角三角形 , 平分交于点 , 取的中点 , 的中点 , 连接 , , , 下列结论:①;②;③;④.其中正确结论有( )
A、 B、 C、 D、12. 如图,在钝角三角形中,分别以和为斜边向的外侧作等腰直角三角形和等腰直角三角形 , 平分交于点 , 取的中点 , 的中点 , 连接 , , , 下列结论:①;②;③;④.其中正确结论有( ) A、1个 B、个 C、个 D、个
A、1个 B、个 C、个 D、个二、填空题(本大题共6小题,每小题4分,共24分)
-
13. 计算的结果等于 .14. 已知 , 则的值是 .15. 已知: ,则 .16. 已知关于的方程、、为常数,的解是 , , 那么方程的解是 .17. 若关于x的方程ax2+2x+1=0有两个不相等的实数根,则实数a的取值范围是 .18. 如图,正方形的边长是3. , 连接、交于点 , 并分别与边、交于点、 , 连接 , 下列到结论:①;②;③;④;⑤当时, , 其中正确结论是: .

三、解答题(本大题共8小题,共78分)
-
19. 用适当的方法解下列方程.(1)、x2-2x=2x+1;(2)、x(x-2)-3x2=-1;20. 计算:21. 如图,△ABC中,AB=9,AC=6,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,求线段EF的长.
 22. 关于 的一元二次方程 有两个不相等的实数根.(1)、求 的取值范围;(2)、当 取满足条件的最大整数时,求方程的根.23. 在平面直角坐标系中,的三个顶点的坐标分别是 , , .
22. 关于 的一元二次方程 有两个不相等的实数根.(1)、求 的取值范围;(2)、当 取满足条件的最大整数时,求方程的根.23. 在平面直角坐标系中,的三个顶点的坐标分别是 , , .
⑴画出关于轴成轴对称的△;
⑵画出以点为位似中心,位似比为的△ .
24. 如图,在平行四边形中, , 点、是对角线上的两点,且 , 的延长线交于点 , 的延长线交于点 . (1)、求的长;(2)、设的面积为 , 求四边形的面积.(用含的代数式表示)25. 某商场销售一批鞋子,平均每天可售出40双,每双盈利50元.为了扩大销售,增加盈利,商场决定采取降价措施,调查发现,每双鞋子每降价1元,商场平均每天可多售出2双.(1)、若每双鞋子降价20元,商场平均每天可售出多少双鞋子?(2)、若商场每天要盈利2448元,且让顾客尽可能多得实惠,每双鞋子应降价多少元?(3)、每双鞋子售价多少元时?每天可以获得最大利润。最大利润为多少元?26. 如图,在菱形中, , 点在射线上,连接 , 绕点顺时针旋转,旋转后得到的线段与对角线交于点 , 旋转角 . 射线与射线交于点 .
(1)、求的长;(2)、设的面积为 , 求四边形的面积.(用含的代数式表示)25. 某商场销售一批鞋子,平均每天可售出40双,每双盈利50元.为了扩大销售,增加盈利,商场决定采取降价措施,调查发现,每双鞋子每降价1元,商场平均每天可多售出2双.(1)、若每双鞋子降价20元,商场平均每天可售出多少双鞋子?(2)、若商场每天要盈利2448元,且让顾客尽可能多得实惠,每双鞋子应降价多少元?(3)、每双鞋子售价多少元时?每天可以获得最大利润。最大利润为多少元?26. 如图,在菱形中, , 点在射线上,连接 , 绕点顺时针旋转,旋转后得到的线段与对角线交于点 , 旋转角 . 射线与射线交于点 .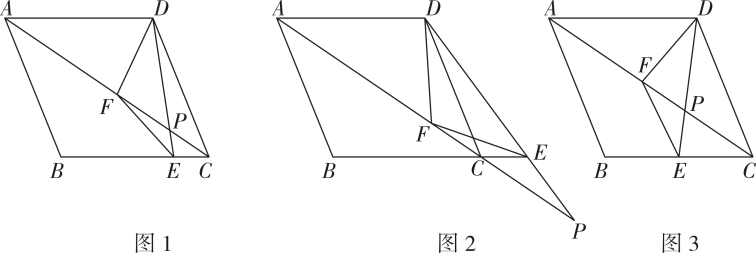 (1)、如图1,当点在线段上时,求证: .(2)、如图2,点在线段的延长线上,当时,求线段的长.(3)、如图3,连接 , 当时,求线段的长.
(1)、如图1,当点在线段上时,求证: .(2)、如图2,点在线段的延长线上,当时,求线段的长.(3)、如图3,连接 , 当时,求线段的长.