湖南省长沙市长郡教育集团2023-2024学年九年级上学期期中数学试卷
试卷更新日期：2023-12-25 类型：期中考试
一、选择题（在下列各题的四个选项中，只有一项是符合题意的.请在答题卡中填涂符合题意的选项.本大题共10个小题，每小题3分，共30分）
-
1. 下列各数中，是无理数的是（ ）A、 B、0 C、 D、-32. 某新闻媒体发布“王亚平成为中国首位出舱的女航天员”，据不完全统计，总播放量超过29600000次，将数据29600000用科学记数法表示为（ ）A、 B、 C、 D、3. 下列事件是必然事件的是（ ）A、四边形内角和是360° B、校园排球比赛，九年一班获得冠军 C、掷一枚硬币时，正面朝上 D、打开电视，正在播放神舟十六号载人飞船发射实况4. 中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录，如图四幅作品分别代表“立春”，“立夏”“芒种”“大雪”，其中既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
5. 要使二次根式有意义，则x的取值范围是（ ）A、x≤-2 B、x≥-2 C、 D、6. 不等式组的解集在数轴上表示为（ ）A、
B、
C、
D、
7. 如图，线段是的直径，于点E ， 若长为16，长为6，则半径是（ ）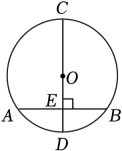
A、5 B、6 C、8 D、108. 已知一个扇形的圆心角为150°，半径是6，则这个扇形的面积是（ ）A、15π B、10π C、5π D、2.5π9. 在同一平面内，点P到圆上的点的最大距离为6，最小距离为4，则此圆的半径为（ ）A、2 B、5 C、1 D、5或110. 如图所示是抛物线y＝ax2+bx+c（a≠0）的部分图象，其顶点坐标为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间，则下列结论：①a-b+c＜0；②3a+c＞0；③b2＝4a（c-n）；④一元二次方程ax2+bx+c-n-2＝0没有实数根．其中正确的结论个数是（ ）
A、1个 B、2个 C、3个 D、4个二、填空题（本大题共有6小题，每小题3分，共18分.）
-
11. 已知M（a，3）和N（-4，b）关于原点对称，则a+b＝ ．12. 在一个不透明的箱子里放有7个红球和3个黑球，它们除颜色外其余都相同．从这个箱子里随机摸出一个球，摸出的球是红球的概率是 ．13. 一元二次方程2x2-mx+3＝0的一根为3，则m的值为 ．14. 如图，在⊙O中，弦BC＝2，点A是圆上一点，且∠BAC＝30°，则⊙O的半径是 ．
15. 如图，将三角形 绕点 顺时针旋转得到三角形 ，若点 恰好在 的延长线上，若 ，则 的度数为.
16. 如图，二次函数y=ax2+bx+c的图象与x轴交于（﹣2，0）和（4，0）两点，当函数值y＞0时，自变量x的取值范围是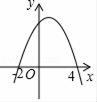
三、解答题（本大题共有9小题，第17、18、19题每小题6分，第20、21题每小题6分，第22、23题每小题6分，第24、25题每小题6分，共72分.请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）
-
17. 计算： ．18. 先化简，再求值： ， 其中x＝5．19. 如图，在平面直角坐标系内，△ABC三个顶点的坐标分别为A（1，-2），B（4，-1），C（3，-3）（网格中，每个小正方形的边长都是1个单位长度）．
(1)、以坐标原点O为旋转中心，将△ABC逆时针旋转90°，得到△A1B1C1 ， 请画出△A1B1C1 ， 写出点A1的坐标；(2)、求旋转过程中点C经过的路径长．20. 2022年虎年新春，中国女足3：2逆转韩国，时隔16年再夺亚洲杯总冠军：2022年国庆，中国女篮高歌猛进，时隔28年再夺世界杯亚军，展现了中国体育的风采！为了培养青少年体育兴趣、体育意识，某校初中开展了“阳光体育活动”，决定开设篮球、足球、乒乓球、羽毛球、排球这五项球类活动，为了了解学生对这五项活动的喜爱情况，随机调查了一些学生（每名学生必选且只能选择这五项活动中的一种）．根据以下统计图提供的信息，请解答下列问题：
(1)、本次被调查的学生有 ▲ 名，补全条形统计图；(2)、扇形统计图中“羽毛球”对应的扇形的圆心角度数是 ；(3)、学校准备推荐甲、乙、丙、丁四名同学中的2名参加全市中学生篮球比赛，则甲和乙同学同时被选中的概率是多少？21. 如图，在平面直角坐标系中，已知抛物线y＝ax2+bx-4 过点（3，-4），与x轴相交于A，B两点，与y轴相交于C点，点A的坐标为（-1，0）．
(1)、求抛物线的解析式及其对称轴；(2)、点P是直线BC下方抛物线上一动点，过点P作y轴平行线交直线BC于点Q，求线段PQ的最大值及此时点P的坐标．22. “一盔一带”安全守护行动是公安部在全国开展的一项安全守护行动，也是营造文明城市，做文明市民的重要标准，“一盔”是指安全头盔，电动自行车驾驶人和乘坐人员应当戴安全头盔，某商场欲购进一批头盔，已知购进8个甲型头盔和6个乙型头盔需要630元，购进6个甲型头盔和8个乙型头盔需要700元．(1)、购进1个甲型头盔和1个乙型头盔分别需要多少元？(2)、若该商场准备购进200个这两种型号的头盔，总费用不超过10200元，以甲型头盔58元/个、乙型头盔98元/个的价格销售完．要使总利润不少于6180元，有多少种进货方案？其中利润最大的方案是甲型头盔和乙型头盔各多少个？最大利润是多少？23. 新定义：已知y是x的函数，若函数图象上存在一点P（a，a+2），则称点P为函数图象上的“朴实点”．例如：直线y＝2x+1上存在的“朴实点”是P（1，3）．(1)、判断直线y＝x+4上是否有“朴实点”？若有，直接写出其坐标；若没有，请说明理由；(2)、若抛物线y＝x2+3x+2-k上存在两个“朴实点”，两个“朴实点”之间的距离为2 ， 求k的值；(3)、若二次函数y＝x2+（m-t+1）x+2n+2t-2的图象上存在唯一的“朴实点”，且当-2≤m≤3时，n的最小值为t+4，求t的值．24. 如图，△ABC内接于⊙O，AC＝BC，弦CD与AB交于点E， ， 过点A作AF⊥BC于点F．
(1)、判断∠ABC与∠ABD的大小关系，并说明理由；(2)、求证：AC＝2CF+BD；(3)、若 S△CFA＝S△CBD ， 求的值．