山东省青岛市市南区2023-2024学年八年级上学期期中数学试卷
试卷更新日期:2023-12-25 类型:期中考试
一、选择题(共8小题,满分24分,每小题3分)
-
1. 下列图各组数中,是勾股数的是( )A、6,8,12 B、0.6,0.8,1 C、8,15,16 D、9,12,152. 下列条件中,不能判定△ABC是直角三角形的是( )A、∠A=∠B+∠C B、a:b:c=5:12:13 C、a2=(b+c)(b-c) D、∠A:∠B:∠C=3:4:53. 如图,“赵爽弦图”是用四个相同的直角三角形与一个小正方形无缝隙地铺成一个大正方形,已知大正方形面积为25,(x+y)2=49,用x,y表示直角三角形的两直角边(x>y),下列选项中正确的是( )
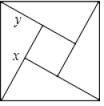 A、小正方形面积为4 B、x2+y2=5 C、x2-y2=7 D、xy=244. 如图,数轴上点A所表示的实数是( )
A、小正方形面积为4 B、x2+y2=5 C、x2-y2=7 D、xy=244. 如图,数轴上点A所表示的实数是( )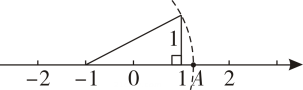 A、 B、 C、 D、25. 下列计算正确的是( )A、 B、 C、 D、6. 点P(a-2,a+1)在x轴上,则a的值为( )A、2 B、0 C、1 D、-17. 一条公路旁依次有A,B,C三个村庄,甲、乙两人骑自行车分别从A村、B村同时出发前往C村,甲、乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,下列结论:①A,B两村相距10km;②甲出发2h后到达C村;③甲每小时比乙多骑行8km;④相遇后,乙又骑行了30min或55min时两人相距4km.其中正确的是( )
A、 B、 C、 D、25. 下列计算正确的是( )A、 B、 C、 D、6. 点P(a-2,a+1)在x轴上,则a的值为( )A、2 B、0 C、1 D、-17. 一条公路旁依次有A,B,C三个村庄,甲、乙两人骑自行车分别从A村、B村同时出发前往C村,甲、乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,下列结论:①A,B两村相距10km;②甲出发2h后到达C村;③甲每小时比乙多骑行8km;④相遇后,乙又骑行了30min或55min时两人相距4km.其中正确的是( ) A、①③④ B、①②③ C、①②④ D、①②③④8. 若直线y=kx+b经过一、二、四象限,则直线y=bx﹣k的图象只能是图中的( )A、
A、①③④ B、①②③ C、①②④ D、①②③④8. 若直线y=kx+b经过一、二、四象限,则直线y=bx﹣k的图象只能是图中的( )A、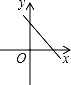 B、
B、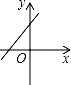 C、
C、 D、
D、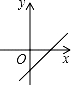
二、填空题(共6小题,满分18分,每小题3分)
-
9. 已知直角三角形的两边长分别为3cm和4cm,则第三边长为 .10. 有一个数值转换器,原理如图所示,当输入x的值为16时,输出y的值是 .
 11. 实数a,b在数轴上的位置如图所示,则|b-a|-|a+b|= .
11. 实数a,b在数轴上的位置如图所示,则|b-a|-|a+b|= . 12. 已知 是一次函数,则m=.13. 如图,在桌面上的长方体ABCD-EFGH中,长AB为8米,宽BC为6米,高BF为4米,点M在棱HG上,且HM=3MG.一只蚂蚁从A点出发沿长方体的表面爬到M点,则它爬行的最短路程为 米.
12. 已知 是一次函数,则m=.13. 如图,在桌面上的长方体ABCD-EFGH中,长AB为8米,宽BC为6米,高BF为4米,点M在棱HG上,且HM=3MG.一只蚂蚁从A点出发沿长方体的表面爬到M点,则它爬行的最短路程为 米. 14. 如图,在平面直角坐标系中,点A1 , A2 , A3 , …都在x轴上,点B1 , B2 , B3 , …都在直线y=x上,OA1=1,且△B1A1A2 , B2A2A3 , B3A3A4 , …,△BnAnAn+1 , …分别是以A1 , A2 , A3 , …,An , …为直角顶点的等腰直角三角形,则△B10A10A11的面积是 .
14. 如图,在平面直角坐标系中,点A1 , A2 , A3 , …都在x轴上,点B1 , B2 , B3 , …都在直线y=x上,OA1=1,且△B1A1A2 , B2A2A3 , B3A3A4 , …,△BnAnAn+1 , …分别是以A1 , A2 , A3 , …,An , …为直角顶点的等腰直角三角形,则△B10A10A11的面积是 .
三、解答题(共9小题,满分78分)
-
15. 计算(1)、;(2)、(3)、(4)、.16. 如图所示,在平面直角坐标系中,已知A(0,1)、B(2,0)、C(4,3).
 (1)、在平面直角坐标系中画出△ABC,则△ABC的面积是 ▲ ;(2)、若点D与点C关于y轴对称,则点D的坐标为 ;(3)、已知P为x轴上一点,若△ABP的面积为1,求点P的坐标.17. 如图,点D在△ABC中,∠BDC=90°,AB=6,AC=BD=4,CD=2.
(1)、在平面直角坐标系中画出△ABC,则△ABC的面积是 ▲ ;(2)、若点D与点C关于y轴对称,则点D的坐标为 ;(3)、已知P为x轴上一点,若△ABP的面积为1,求点P的坐标.17. 如图,点D在△ABC中,∠BDC=90°,AB=6,AC=BD=4,CD=2.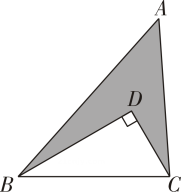 (1)、求BC的长;(2)、求图中阴影部分的面积.18. 已知6a+34的立方根是4,5a+b-2的算术平方根是5,c是9的算术平方根.(1)、求a,b,c的值;(2)、求3a-b+c的平方根.19. 甲、乙两家体育用品商店出售相同的乒乓球和乒乓球拍,乒乓球每盒定价20元,乒乓球拍每副定价100元.现两家商店都搞促销活动,甲店每买一副球拍赠两盒乒乓球,乙店按八折优惠.某俱乐部需购球拍4副,乒乓球盒.(1)、若在甲店购买付款(元),在乙店购买付款(元),分别写出 , 与x的函数关系式.(2)、若该俱乐部需要购买乒乓球30盒,在哪家商店购买合算?20. 甲、乙两车早上从A城车站出发匀速前往B城车站,在整个行程中,两车离开A城的距离s与时间t的对应关系如图所示.
(1)、求BC的长;(2)、求图中阴影部分的面积.18. 已知6a+34的立方根是4,5a+b-2的算术平方根是5,c是9的算术平方根.(1)、求a,b,c的值;(2)、求3a-b+c的平方根.19. 甲、乙两家体育用品商店出售相同的乒乓球和乒乓球拍,乒乓球每盒定价20元,乒乓球拍每副定价100元.现两家商店都搞促销活动,甲店每买一副球拍赠两盒乒乓球,乙店按八折优惠.某俱乐部需购球拍4副,乒乓球盒.(1)、若在甲店购买付款(元),在乙店购买付款(元),分别写出 , 与x的函数关系式.(2)、若该俱乐部需要购买乒乓球30盒,在哪家商店购买合算?20. 甲、乙两车早上从A城车站出发匀速前往B城车站,在整个行程中,两车离开A城的距离s与时间t的对应关系如图所示. (1)、A,B两城之间距离是多少?(2)、求甲、乙两车的速度分别是多少?(3)、乙车出发多长时间追上甲车?(4)、从乙车出发后到甲车到达B城车站这一时间段,在何时间点两车相距40km?21. 小丽根据学习“数与式”积累的经验,想通过“由特殊到一般”的方法探究下面二次根式的运算规律.
(1)、A,B两城之间距离是多少?(2)、求甲、乙两车的速度分别是多少?(3)、乙车出发多长时间追上甲车?(4)、从乙车出发后到甲车到达B城车站这一时间段,在何时间点两车相距40km?21. 小丽根据学习“数与式”积累的经验,想通过“由特殊到一般”的方法探究下面二次根式的运算规律.下面是小丽的探究过程,请补充完整:
(1)、具体运算,发现规律,特例1:
特:2:
特:3:
特例4: . (填写一个符合上述运算特征的例子);
(2)、观察、归纳,得出猜想.如果n为正整数,用含n的式子表示上述的运算规律为:;
(3)、证明你的猜想;(4)、应用运算规律化简:= .22. (1)、如图1,长方体的长为4cm,宽为3cm,高为12cm.求该长方体中能放入木棒的最大长度;(2)、如图2,长方体的长为4cm,宽为3cm,高为12cm.现有一只蚂蚁从点A处沿长方体的表面爬到点G处,求它爬行的最短路程;(3)、若将题中的长方体换成透明圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处.求蚂蚁吃到饭粒需要爬行的最短路程是多少?23. 如图,在平面直角坐标系中,直线y=kx+b与x轴交于点B(-5,0),与y轴交于点A,直线y=-x+4过点A,与x轴交于点C,点P是x轴上方一个动点.
(1)、如图1,长方体的长为4cm,宽为3cm,高为12cm.求该长方体中能放入木棒的最大长度;(2)、如图2,长方体的长为4cm,宽为3cm,高为12cm.现有一只蚂蚁从点A处沿长方体的表面爬到点G处,求它爬行的最短路程;(3)、若将题中的长方体换成透明圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处.求蚂蚁吃到饭粒需要爬行的最短路程是多少?23. 如图,在平面直角坐标系中,直线y=kx+b与x轴交于点B(-5,0),与y轴交于点A,直线y=-x+4过点A,与x轴交于点C,点P是x轴上方一个动点. (1)、求直线AB的函数表达式;(2)、若点P在线段AB上,且S△APC=S△AOB , 求点P的坐标;(3)、当S△PBC=S△AOB时,动点M从点B出发,先运动到点P,再从点P运动到点C后停止运动.点M的运动速度始终为每秒1个单位长度,运动的总时间为t(秒),请直接写出t的最小值.
(1)、求直线AB的函数表达式;(2)、若点P在线段AB上,且S△APC=S△AOB , 求点P的坐标;(3)、当S△PBC=S△AOB时,动点M从点B出发,先运动到点P,再从点P运动到点C后停止运动.点M的运动速度始终为每秒1个单位长度,运动的总时间为t(秒),请直接写出t的最小值.四、附加题(共2小题,满分0分)
-
24. 我们已经学过完全平方公式a2±2ab+b2=(a±b)2 , 知道所有的非负数都可以看作是一个数的平方,如2=()2 , 3=()2 , 7=()2 , 0=02 , 那么,我们可以利用这种思想方法和完全平方公式来计算下面的题:
例:求3-2的算术平方根.
解:3- , ∴3-2的算术平方根是-1.
你看明白了吗?请根据上面的方法化简:
(1)、(2)、(3)、25. 在如图的平面直角坐标系中,直线n过点A(0,-2),且与直线l交于点B(3,2),直线l与y轴交于点C.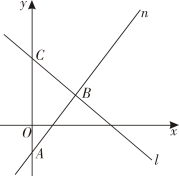 (1)、求直线n的函数表达式;(2)、若△ABC的面积为9,求点C的坐标;(3)、若△ABC是等腰三角形,求直线l的函数表达式.
(1)、求直线n的函数表达式;(2)、若△ABC的面积为9,求点C的坐标;(3)、若△ABC是等腰三角形,求直线l的函数表达式.