安徽省黄山地区2023-2024学年八年级上学期期中考试数学试题

试卷更新日期：2023-12-25 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，满分30分.）

1. 下列图案中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列长度的三条线段能组成三角形的是（）

A、3，4，8 B、5，6，11 C、6，6，6 D、9，9，19

查看试题解析
3. 如图，△ABC≌△DEF，则∠E的度数为（）

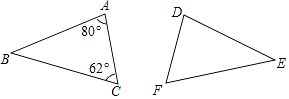A、80° B、40° C、62° D、38°

查看试题解析
4. 如图，在△ABC中，∠B＝55°，∠C＝30°，分别以点A和点C为圆心，大于 $\frac{1}{2}$ AC的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD，则∠BAD的度数为（）

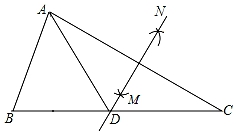A、65° B、60° C、55° D、45°

查看试题解析
5. 如图，已知 $∠ C A B = ∠ D A B$ ，则添加下列一个条件不一定能使△ABC≌△ABD的是（）

A、 $B C = B D$ B、 $∠ C = ∠ D$ C、 $A C = A D$ D、 $∠ A B C = A B D$

查看试题解析
6. 如图，BP是∠ABC的平分线，AP⊥BP于P，连接PC，若△ABC的面积为1cm²则△PBC的面积为（）.

A、0.4 cm² B、0.5 cm² C、0.6 cm² D、不能确定

查看试题解析
7. 如图，在△ABC中，点E和F分别是AC、BC上一点，EF∥AB，∠BCA的平分线交AB于点D，∠MAC是△ABC的外角，若 $∠ M A C = α$ ， $∠ E F C = β$ ， $∠ A D C = γ$ ，则 $α$ 、 $β$ 、 $γ$ 三者间的数量关系是（）

A、 $β = α + γ$ B、 $β = 2 γ - α$ C、 $β = α + 2 γ$ D、 $β = 2 α - 2 γ$

查看试题解析
8. 下列图形中有稳定性的是（）

A、 B、 C、 D、

查看试题解析
9. 如图，△ABC中， $A B = A C$ ， $∠ B = 30 °$ ， AD⊥AB交BC于点D， $A D = 3$ ，则BC的长是（）

A、11 B、10 C、9 D、8

查看试题解析
10. 如图，正△ABC和正△CDE中，B、C、D共线，且 $B C = 3 C D$ ，连接AD和BE相交于点F，以下结论：
① $∠ A F B = 60 °$ ；②连接FC，则FC平分∠BFD；③ $B F = 3 D F$ ；④ $B F = A F + F C$ ．
其中正确的个数是（）

A、4 B、3 C、2 D、1

查看试题解析

二、填空题（本大题共6小题，每空3分，满分21分.）

11. 在平面直角坐标系中，点 $P (- 2 ， 1)$ 关于y轴对称的点的坐标是．

查看试题解析
12. 用一条长18cm的细绳围成一个等腰三角形，若有一边长是8cm，则所围成等腰三角形的底边长为cm．

查看试题解析
13. 已知一张三角形纸片ABC（如图甲），其中 $A B = A C$ ，将纸片沿过点B的直线折叠，使点C落到AB边上的E点处，折痕为BD（如图乙），再将纸片沿过点E的直线折叠，点A恰好与点D重合，折痕为EF（如图丙）．原三角形纸片ABC中，∠ABC的大小为．

查看试题解析
14. 一个n边形的每个外角都等于72°，则 $n =$ ．

查看试题解析
15. 如图，D是AB上一点，DF交AC于点E，E为DF的中点，FC∥AB，若 $B D = 3$ ， $F C = 8$ ，则 $A B =$ ．

查看试题解析
16. 已知在平面直角坐标系中，点 $A (2 ， 0)$ 、 $B (0 ， 3)$ 、 $C (0 ， 2)$ ，点D在第二象限，且△AOB≌△OCD.

(1)、点D的坐标是．

(2)、若点P在y轴上，且△APC为等腰三角形，则满足要求的点P有个．

查看试题解析

三、解答题（本大题共5小题，满分49分.）

17. 已知△ABC中， $∠ B = 2 ∠ A$ ， $∠ C = ∠ A + 20 °$ ，求△ABC各个内角的度数．

查看试题解析
18. 如图 $A E = B D$ ， $A C = D F$ ， $B C = E F$ ，求证：EF∥BC．

查看试题解析
19. 图，AD是△ABC的中线，E是AD上一点，BE交AC于F，若 $E F = A F$ ， $B E = 7.5$ ， $C F = 6$ ，求线段EF的长度.

查看试题解析
20. 如图，在△ABC中， $A B = A C$ ，点D、E、F分别在边AB、BC、AC上，且 $B E = C F$ ， $B D = C E$ ．

(1)、求证：△DEF是等腰三角形；

(2)、当 $∠ A = 40 °$ 时，求∠DEF的度数．

查看试题解析
21. 如图，是一个8×10正方形格纸，△ABC中A点坐标为 $(- 2 ， 1)$ ， B点的坐标为 $(- 1 ， 2)$ ．
⑴请在图中建立平面直角坐标系，并指出△ABC和△ $A^{'} B^{'} C^{'}$ 关于哪条直线对称（直接写答案）？
⑵作出△ABC关于x轴的对称图形△A₁B₁C₁；
⑶若点M在x轴上，当△ $A B^{'} M$ 的周长最小时，点M的坐标为．

查看试题解析
22. 如图，已知点A、C分别在∠GBE的边BG、BE上，且 $A B = A C$ ， BD平分∠GBE，AD∥BE，连接CD．
求证：

(1)、 $A B = A D$ ；

(2)、CD平分∠ACE．

查看试题解析
23. 如图

(1)、如图①，在△ADC中，DP、CP分别平分∠ADC和∠ACD，请直接写出∠P 与∠A的数量关系：．

(2)、如图②，四边形ABCD中，DP、CP分别平分∠ADC、∠BCD，∠P与∠A+∠B有怎样的数量关系？请证明你的结论．

查看试题解析