安徽省宿州市埇桥区教育集团2023-2024学年九年级上学期期中数学试题
试卷更新日期:2023-12-25 类型:期中考试
一、选择题(本大题共10小题,每小题4分,满分40分)
-
1. 下列说法:
①四边相等的四边形一定是菱形
②顺次连接矩形各边中点形成的四边形一定是正方形
③对角线相等的四边形一定是矩形
④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分
其中正确的有( )个.
A、4 B、3 C、2 D、12. 下列方程中,是一元二次方程的是( )A、2x+1=0 B、x2+1=0 C、y2+x=1 D、+x2=13. 若 , 则的值为( )A、1 B、 C、 D、4. 一个家庭有两个孩子,两个都是男孩的概率是( )A、 B、 C、 D、无法确定5. 下列说法中,错误的是A、所有的等边三角形都相似 B、和同一图形相似的两图形相似 C、所有的等腰直角三角形都相似 D、所有的矩形都相似6. 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( ) A、 B、 C、5 D、47. 若关于x的一元二次方程方程有两个不相等的实数根,则k的取值范围是( )A、 B、 , 且 C、 , 且 D、8. 如图,点D,E分别在的AB,AC边上,增加下列条件中的一个:① , ② , ③ , ④ , ⑤ , 使与一定相似的有( )
A、 B、 C、5 D、47. 若关于x的一元二次方程方程有两个不相等的实数根,则k的取值范围是( )A、 B、 , 且 C、 , 且 D、8. 如图,点D,E分别在的AB,AC边上,增加下列条件中的一个:① , ② , ③ , ④ , ⑤ , 使与一定相似的有( )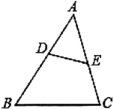 A、①②④ B、②④⑤ C、①②③④ D、①②③⑤9. 我们知道,四边形具有不稳定性,如图,在平面直角坐标系中,边长为2的正方形的边在x轴上,的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点处,则点C的对应点的坐标为( )
A、①②④ B、②④⑤ C、①②③④ D、①②③⑤9. 我们知道,四边形具有不稳定性,如图,在平面直角坐标系中,边长为2的正方形的边在x轴上,的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点处,则点C的对应点的坐标为( )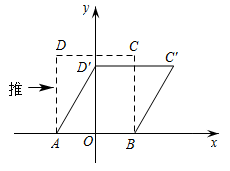 A、 B、 C、 D、10. 已知菱形ABCD的两条对角线长分别为6和8,M、N分别是边BC,CD的中点,P是对角线BD上一点,则的最小值为( )
A、 B、 C、 D、10. 已知菱形ABCD的两条对角线长分别为6和8,M、N分别是边BC,CD的中点,P是对角线BD上一点,则的最小值为( )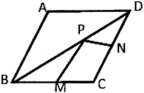 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题(本大题共4小题,每小题5分,满分20分)
-
11. 若3是关于x的方程的一个根,则方程的另一个根等于 .12. 如图所示,矩形ABCD两条对角线夹角为 , , 则对角线AC长为 .
 13. 从 三个数中任取两个不同的数作为点的坐标,则该点在坐标轴上的概率是 .14. 四边形ABCD是边长为4的正方形,点E在边AD所在的直线上,连接CE,以CE为边,作正方形CEFG(点D,点F在直线CE的同侧),连接BF.
13. 从 三个数中任取两个不同的数作为点的坐标,则该点在坐标轴上的概率是 .14. 四边形ABCD是边长为4的正方形,点E在边AD所在的直线上,连接CE,以CE为边,作正方形CEFG(点D,点F在直线CE的同侧),连接BF.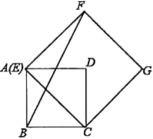
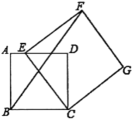
图1 图2
(1)、如图1,当点E与点A重合时,;(2)、如图2,当点E在线段AD上时, , 则 .三、(本大题共2小题,每小题8分,满分16分)
-
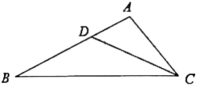
15. 解方程:(1)、(2)、16. 如图,在中,点D是AB上一点,且 , , .
求证: .
四、(本大题共2小题,每小题8分,满分16分)
-
17. 如图是的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹,不需要证明).
图1
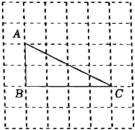 图2
图2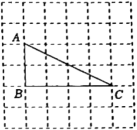 (1)、如图1,在边BC上找一点P,使得;(2)、如图2,在边AC上找一点Q,使得B.18. 已知等腰三角形的一边长为9,另一边长为方程的根,求该等腰三角形的周长.
(1)、如图1,在边BC上找一点P,使得;(2)、如图2,在边AC上找一点Q,使得B.18. 已知等腰三角形的一边长为9,另一边长为方程的根,求该等腰三角形的周长.五、(本大题共2小题,每小题10分,满分20分)
-
19. 如图,在▱ABCD中,已知E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
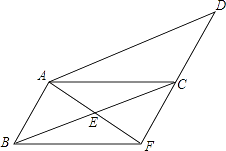 (1)、求证:AB=CF;(2)、当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.20. 如图所示,已知在中, , , , 点Q从点A开始沿AB边向点B以的速度移动,点P从点B开始沿BC边向点C以的速度移动.
(1)、求证:AB=CF;(2)、当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.20. 如图所示,已知在中, , , , 点Q从点A开始沿AB边向点B以的速度移动,点P从点B开始沿BC边向点C以的速度移动.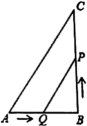 (1)、如果Q、P分别从A、B两点出发,那么几秒后,的面积等于?(2)、在(1)中,的面积能否等于?试说明理由.
(1)、如果Q、P分别从A、B两点出发,那么几秒后,的面积等于?(2)、在(1)中,的面积能否等于?试说明理由.六、(本题满分12分)
-
21. 某校在一次大课间活动中,采用了四种活动形式:A、跑步,B、跳绳,C、做操,D、游戏.全校学生都选择了一种形式参与活动,小杰对同学们选用的活动形式进行了随机抽样调查,根据调查统计结果,绘制了不完整的统计图.

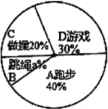
请结合统计图,回答下列问题:
(1)、本次调查学生共 ▲ 人, ▲ , 并将条形图补充完整;(2)、如果该校有学生2000人,请你估计该校选择“跑步”这种活动的学生约有多少人?(3)、学校让每班在A、B、C、D四种活动形式中,随机抽取两种开展活动,请用树状图或列表的方法,求每班抽取的两种形式恰好是“跑步”和“跳绳”的概率.七、(本题满分12分)
-
22. 每年某购物网站都会举办“双十一”购物活动,许多商家都会利用这个契机进行打折让利的促销活动.甲网店销售一件A商品成本为50元,网上标价80元.(1)、“双十一”购物活动当天,甲网店连续两次降价销售A商品吸引买主,问平均每次降价率为多少,才能使这件A商品的售价为51.2元?(2)、据媒体爆料,有一些淘宝商家在“双十一”购物活动当天,先提高商品的网上标价后再推出促销活动,存在欺诈行为.“双十一”活动之前,乙网店销售A商品的成本、网上标价与甲网店一致,一周可售出1000件A商品.在“双十一”购物活动这天,乙网店先将网上标价提高a%,再推出五折销售的促销活动,吸引了大量网购者,乙网店在“双十一”购物活动当天卖出的A商品数量也比原来一周卖出的A商品数量增加了2a%,这样“双十一”活动当天乙网店的利润达到了2万元,求乙网店在“双十一”购物活动这天的网上标价为多少?
八、(本题满分14分)
-
23. 是等边三角形,点D是射线BC上的一个动点(点D不与点B、C重合),是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB、AC于点F、G,连接BE.
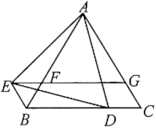

图(a) 图(b)
(1)、如图(a)所示,当点D在线段BC上时.①求证:;
②探究四边形BCGE是怎样特殊的四边形?并说明理由;
(2)、如图(b)所示,当点D在BC的延长线上时,直接写出(1)中的两个结论是否成立?(3)、在(2)的情况下,当点D运动到什么位置时,四边形BCGE是菱形?并说明理由.
-
-