【浙教版】数学八年级上册期末冲刺满分攻略16 函数基础知识
试卷更新日期:2023-12-25 类型:复习试卷
一、选择题
-
1. 下列关系式中,y不是x的函数的是( )A、 B、 C、 D、2. 函数y= 中自变量x的取值范围是( )A、x≠-2 B、x≠2 C、x<2 D、x>23. 下列图象中,表示y是x的函数的个数有( )
 A、1 B、2个 C、3个 D、4个4. 某辆速度为v(km/h)的车从甲地开往相距s(km)的乙地,全程所用的时间为t(h),在这个变化过程中,( )A、s是变量 B、t是常量 C、v是常量 D、s是常量5. 下列函数中,自变量的取值范围选取错误的是( )A、y=2x2中,x取全体实数 B、y=中,x取x≠-1的实数 C、y=中,x取x≥2的实数 D、y=中,x取x≥-3的实数6. 台州市2023年中考体育排球项目考试的评分标准如下表:
A、1 B、2个 C、3个 D、4个4. 某辆速度为v(km/h)的车从甲地开往相距s(km)的乙地,全程所用的时间为t(h),在这个变化过程中,( )A、s是变量 B、t是常量 C、v是常量 D、s是常量5. 下列函数中,自变量的取值范围选取错误的是( )A、y=2x2中,x取全体实数 B、y=中,x取x≠-1的实数 C、y=中,x取x≥2的实数 D、y=中,x取x≥-3的实数6. 台州市2023年中考体育排球项目考试的评分标准如下表:个数
分值
10
9
8
7
6
个数
分值
5
4
3
2
1
现有两种说法:①是的函数;②是的函数.下列判断正确的是( )
A、①对,②错 B、①错,②对 C、①对,②对 D、①错,②错7. 甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙走完全程用了36分钟;③乙用16分钟追上甲;④乙到达终点时,甲离终点还有300米.其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个8. 早上9点,甲车从地出发去地,20分钟后,乙车从地出发去地.两车离开各自出发地的路程(千米)与时间(小时)的函数关系如图所示,下列描述中不正确的是( )
A、1个 B、2个 C、3个 D、4个8. 早上9点,甲车从地出发去地,20分钟后,乙车从地出发去地.两车离开各自出发地的路程(千米)与时间(小时)的函数关系如图所示,下列描述中不正确的是( ) A、两地相距240千米 B、乙车平均速度是90千米/小时 C、乙车在12:00到达地 D、甲车与乙车在早上10点相遇9. 在直角三角形ABC中, , , , 则y与x之间的函数关系式是( )A、
A、两地相距240千米 B、乙车平均速度是90千米/小时 C、乙车在12:00到达地 D、甲车与乙车在早上10点相遇9. 在直角三角形ABC中, , , , 则y与x之间的函数关系式是( )A、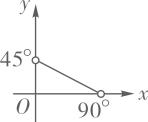 B、
B、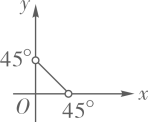 C、
C、 D、
D、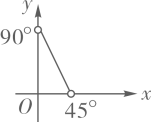 10. 如图,小明使用图形计算器探究函数的图象,他输入了一组a,b的值,得到了下面的函数图象,由学习函数的经验,可以推断出小明输入的a,b的值满足( )
10. 如图,小明使用图形计算器探究函数的图象,他输入了一组a,b的值,得到了下面的函数图象,由学习函数的经验,可以推断出小明输入的a,b的值满足( ) A、a>0,b>0 B、a>0,b<0 C、 D、
A、a>0,b>0 B、a>0,b<0 C、 D、二、填空题
-
11. 三角形的面积公式中S=ah其中底边a保持不变,则常量是 ,变量是 .12. 如图,某链条每节长为 , 每两节链条相连接部分重叠的圆的直径为 , 按这种连接方式,x节链条总长度为 , 则y关于x的函数关系式是.
 13. 在直角坐标系中,有A(3,﹣3),B(5,3)两点,现另取一点C(1,n),当△ABC周长最小时,n的值是 .14. 某公司准备与汽车租赁公司签订租车合同,以每月用车路程x(千米)计算,甲汽车租赁公司每月收取的租赁费为y1元,乙汽车租赁公司每月收取的租赁费为y2元,y1 , y2与x之间的函数关系如图所示.当月用车路程为2300千米时,选汽车租赁公司比较合算.
13. 在直角坐标系中,有A(3,﹣3),B(5,3)两点,现另取一点C(1,n),当△ABC周长最小时,n的值是 .14. 某公司准备与汽车租赁公司签订租车合同,以每月用车路程x(千米)计算,甲汽车租赁公司每月收取的租赁费为y1元,乙汽车租赁公司每月收取的租赁费为y2元,y1 , y2与x之间的函数关系如图所示.当月用车路程为2300千米时,选汽车租赁公司比较合算. 15. 函数 的自变量x取值范围是16. 如图1,在中,动点从点出发沿折线匀速运动至点后停止.已知点的运动速度是每秒2个单位长度,设点运动时间为 , 线段的长度为 , 图2是与的函数关系的大致图象,其中点为曲线的最低点,则的高长是.
15. 函数 的自变量x取值范围是16. 如图1,在中,动点从点出发沿折线匀速运动至点后停止.已知点的运动速度是每秒2个单位长度,设点运动时间为 , 线段的长度为 , 图2是与的函数关系的大致图象,其中点为曲线的最低点,则的高长是.
三、解答题
-
17. 当x=2及x=﹣3时,分别求出下列函数的函数值:
(1)y=(x+1)(x﹣2);
(2)y= .
18. 如图,等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.试写出重叠部分的面积y cm2与MA的长度x cm之间的关系式,并指出其中的常量与变量. 19. 如表是某报纸公布的世界人口数据情况:
19. 如表是某报纸公布的世界人口数据情况:年份
1957
1974
1987
1999
2010
2025
人口数
30亿
40亿
50亿
60亿
70亿
80亿
(1)表中有几个变量?
(2)如果要用x表示年份,用y表示世界人口总数,那么随着x的变化,y的变化趋势是怎样的?
20. 物体自由下落的高度h(米)和下落时间t(秒)的关系是:在地球上大约是h=4.9t2 , 在月球上大约是h=0.8t2 , 当h=20米时,(1)物体在地球上和在月球上自由下落的时间各是多少?
(2)物体在哪里下落得快?
21. 如图,正方形EFGH的四个顶点分别在边长为1的正方形ABCD的四条边上. (1)、设 , 试求正方形EFGH的面积y关于x的函数式,并写出自变量x的取值范围;(2)、当时,求正方形EFGH的面积.22. 如图,小赵和小李相约去农庄游玩.小李从小区甲骑电动车出发.同时,小赵从小区乙开车出发,途中,他去超市买了一些东西后,按原来的速度继续去农庄,小区甲、乙、超市和农庄之间的路程图所示,设他们离小区甲的路程为s(km),出发的时间为t(分).根据下图回答问题:
(1)、设 , 试求正方形EFGH的面积y关于x的函数式,并写出自变量x的取值范围;(2)、当时,求正方形EFGH的面积.22. 如图,小赵和小李相约去农庄游玩.小李从小区甲骑电动车出发.同时,小赵从小区乙开车出发,途中,他去超市买了一些东西后,按原来的速度继续去农庄,小区甲、乙、超市和农庄之间的路程图所示,设他们离小区甲的路程为s(km),出发的时间为t(分).根据下图回答问题: (1)、点A的坐标为 , 小赵的开车速度为km/分;(2)、求线段CB的函数表达式,并写出自变量t的取值范围(3)、求小赵离开超市后追上小李时,距离农庄多少km?23. 某游泳池的平面图如图1,宽30米,深水区长40米,浅水区长8米.游泳池应定期换水.图2是小明给游泳池放水时,游泳池的存水量Q(立方米)与放水时间t(小时)的函数图象.其中表示正好放到浅水区底部时的状态.
(1)、点A的坐标为 , 小赵的开车速度为km/分;(2)、求线段CB的函数表达式,并写出自变量t的取值范围(3)、求小赵离开超市后追上小李时,距离农庄多少km?23. 某游泳池的平面图如图1,宽30米,深水区长40米,浅水区长8米.游泳池应定期换水.图2是小明给游泳池放水时,游泳池的存水量Q(立方米)与放水时间t(小时)的函数图象.其中表示正好放到浅水区底部时的状态.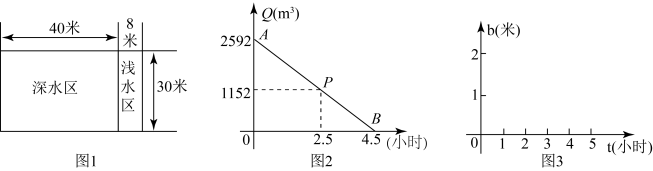 (1)、观察图1,图2.可知:深水区的面积是平方米,浅水区的面积是平方米,放水速度是每小时立方米;(2)、求Q关于t的函数表达式,并写出自变量t的取值范围;(3)、游泳池清理干净后,又将水放到原来的高度.若进水速度与放水速度相同,请在图3中,画出游泳池中的水深h(米)关于进水时间t(小时)的函数图象(请标注关键点的坐标).
(1)、观察图1,图2.可知:深水区的面积是平方米,浅水区的面积是平方米,放水速度是每小时立方米;(2)、求Q关于t的函数表达式,并写出自变量t的取值范围;(3)、游泳池清理干净后,又将水放到原来的高度.若进水速度与放水速度相同,请在图3中,画出游泳池中的水深h(米)关于进水时间t(小时)的函数图象(请标注关键点的坐标).