【浙教版】2023-2024学年数学八年级上册期末冲刺满分攻略14 有序数对与平面直角坐标系

试卷更新日期：2023-12-25 类型：复习试卷

进入出卷网下载

一、选择题

1. 点 $P (- 1 ， 3)$ 所在的象限为（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 根据下列表述，不能确定具体位置的是（）

A、某电影院1号厅的3排4座 B、慈溪市孙塘北路824号 C、某灯塔南偏西30°方向 D、东经108°，北纬53°

查看试题解析
3. 在平面直角坐标系中，点M（m-1，2m）在x轴上，则点M的坐标是（）

A、（1，0） B、（-1，0） C、（0，2） D、（0，-1）

查看试题解析
4. 如图是中国象棋棋盘的一部分，建立如图所示的平面直角坐标系，已知“車”所在位留的坐标为 $(- 2 ， 2)$ ，则“炮”所在位置的坐标为（）．

A、 $(3 ， 1)$ B、 $(1 ， 3)$ C、 $(4 ， 1)$ D、 $(3 ， 2)$

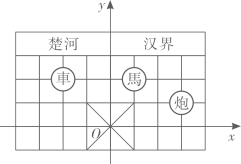查看试题解析
5. 在平面直角坐标系中，已知点 $P (3 ， a)$ 到x轴的距离为2，则a的值为（）

A、2 B、-2 C、±2 D、不能确定

查看试题解析
6. 在平面直角坐标系中，点A（a ， a²-1）在第二象限内，则a的取值可以是（）

A、 $- \frac{1}{2}$ B、 $- \frac{3}{2}$ C、 $\frac{1}{2}$ D、 $\frac{3}{2}$

查看试题解析
7.
如图，动点P从（0，3）出发，沿所示方向运动，每当碰到矩形的边时反弹，反弹时反射角等于入射角，当点P第2014次碰到矩形的边时，点P的坐标为（　　）

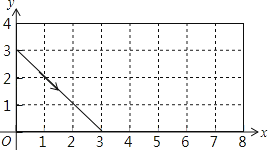A、（1，4） B、（5，0） C、（6，4） D、（8，3）

查看试题解析
8. 有甲、乙、丙三人，它们所在的位置不同，他们三人都以相同的单位长度建立不同的平面直角坐标系，甲说：“如果以我为坐标原点，乙的位置是(4，3)．”丙说：“如果以我为坐标原点，乙的位置是(-3，-4)．”如果以乙为坐标原点，那么甲和丙的位置分别是（）

A、(3，4)，(-3，-4) B、(4，-3)，(3，-4) C、(-3，-4)，(4，3) D、(-4，-3)，(3，4)

查看试题解析
9. 用大小完全相同的长方形在直角坐标系中摆成如图所示图案，已知点A的坐标为（-14，6)，则点B的坐标是（）

A、 $(1 ， - 7)$ B、 $(- 1 ， 7)$ C、 $(2 ， - 10)$ D、 $(- 2 ， 10)$

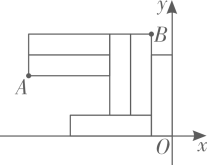查看试题解析
10. 中国象棋中“马走日字”（“马”从两个小方格组成的“日”字的一角走到相对的另一对角，横着走竖着走都可以），如“马”从点 $P (1 ， 0)$ 出发，可到达A，B，C，D，E，F中任意一点，若“马”从点P出发连续走了n次“日”字后到达点 $Q (16 ， 12)$ ，则n的最小值为（）

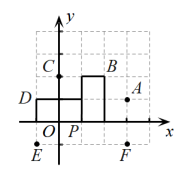A、6 B、7 C、8 D、9

查看试题解析

二、填空题

11. 在如图所示的方格纸上建立适当的平面直角坐标系，若点 $A$ 的坐标为 $(0 ， 1)$ ，点 $B$ 的坐标为 $(2 ， 2)$ ，则点 $C$ 的坐标为.

查看试题解析
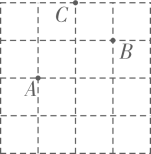12. 点 $A (3 - a ， 2 a - 4)$ 在x轴上，则点A的坐标是．

查看试题解析
13. 在平面直角坐标系中，点 $A$ 在 $x$ 轴上，且位于原点右侧，距离原点3个单位长度，则点 $A$ 的坐标为.

查看试题解析
14. 如图，玉环漩门湾农业观光园的示意图的三个地点刚好在网格的格点上，若神农广场的坐标为 $(- 3 ， 0)$ ，游客中心的坐标为 $(2 ， 1)$ ，则农展馆的坐标为．

查看试题解析
15. 若点A的坐标（x，y）满足条件(x－3)²＋ $\sqrt{y + 2}$ ＝0，则点A在第象限

查看试题解析
16. 如图，正方形 $O A_{1} B_{1} C_{1}$ ， $C_{1} A_{2} B_{2} C_{2}$ ， $C_{2} A_{3} B_{3} C_{3}$ ， …的顶点 $A_{1} ， A_{2} ， A_{3}$ ， …在直线 $y = k x + b$ 上，顶点 $C_{1}$ ， $C_{2}$ ， $C_{3}$ ， …在x轴上，已知 $B_{1} (1 ， 1)$ ， $B_{2} (3 ， 2)$ ，那么点 $A_{8}$ 的坐标为.

查看试题解析

三、解答题

17. 在平面直角坐标系中，点A，B的坐标分别为 $A (- 1 ， 3)$ ， $B (- 2 ， - 1)$ ，将线段 $A B$ 向右平移4单位，向下平移1单位，平移后A对应D，B对应C，

(1)、在如图直角坐标系中，画出这个四边形 $A B C D$ .

(2)、写出点C、D的坐标，则C ， D.

(3)、四边形 $A B C D$ 的周长为.

查看试题解析
18. 如图，在平面直角坐标系中，有一个三角形ABC，点A'的坐标是（-2，2)，现将三角形ABC平移，使点A变换为点A'，点B'，C"分别是点B，C的对应点.

(1)、请画出平移后的三角形A'B'C'(不写画法），并直接写出点B'，C'的坐标；

(2)、若三角形ABC内部有一点P，其平移后的对应点为P'(-2，1)，则点P的坐标是.

查看试题解析
19. 在平面直角坐标系中，已知点 $P (m - 3 ， 5 - 2 m)$ ， m是任意实数.

(1)、当 $m = 0$ 时，点P在第几象限？

(2)、当点P在第三象限时，求m的取值范围.

(3)、判断命题“点P不可能在第一象限”的真假，并说明理由.

查看试题解析
20. 已知点P（-3a-4，2+a），解答下列各题：

(1)、若点P在x轴上，则点P的坐标为P；

(2)、若Q（5，8），且PQ∥y轴，则点P的坐标为P；

(3)、若点P在第二象限，且它到x轴、y轴的距离相等，求a²⁰²⁰+2021的值.

查看试题解析
21. 温州一位老人制作的仿真郑和宝船尺寸如图，已知在某一直角坐标系中点A坐标为（9，0），请你直接在图中画出该坐标系，并写出其余5点的坐标．

查看试题解析
22. 在某河流的北岸有A、B两个村子，A村距河北岸的距离为1千米，B村距河北岸的距离为4千米，且两村相距5千米，B在A的右边，现以河北岸为x轴，A村在y轴正半轴上（单位：千米）.

(1)、请建立平面直角坐标系，并描出A、B两村的位置，写出其坐标.

(2)、近几年，由于乱砍滥伐，生态环境受到破坏，A、B两村面临缺水的危险.两村商议，共同在河北岸修一个水泵站，分别向两村各铺一条水管，要使所用水管最短，水泵站应修在什么位置在图中标出水泵站的位置，并求出所用水管的长度.

查看试题解析
23. 对于平面直角坐标中的任意两点P，Q，若点P到两坐标轴的距离之和等于点Q到两坐标轴的距离之和，则称P，Q两点为“和合点”，如图1中的P，Q两点即为“和合点”．

(1)、已知点 $A (- 4 ， 8)$ ， $B (6 ， 0)$ ， $C (6 ， 6)$ ， $D (- 2 ， 9)$ ．
①在上面四点中，与点 $E (- 5 ， - 7)$ 为“和合点”的是 ▲ ；
②若点 $F (- 3 ， 0)$ ，过点F作直线 $l ⊥ x$ 轴，点G直线l上，A、G两点为“和合点”，则点G的坐标为 ▲ ；
③若点 $M (2 a ， 3 b)$ 在第二象限，点 $N (- 3 a ， - b)$ 在第四象限，且A、M两点为“和合点”，D、N两点为“和合点”，求a，b的值．

(2)、如图2，已知点 $H (- 5 ， 0)$ ， $K (0 ， 5)$ ，点 $R (x ， y)$ 是线段 $H K$ 上的一动点，且满足 $x - y = - 5$ ，过点 $T (n ， 0)$ 作直线 $m ⊥ x$ 轴，若在直线m上存在点S，使得R，S两点为“和合点”，直接写出n的取值范围．

查看试题解析