广西壮族自治区玉林市容县2023-2024学年七年级上学期期中数学试卷

试卷更新日期：2023-12-24 类型：期中考试

进入出卷网下载

一、选择题：本大题共12小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的，将正确答案涂在答题卡相应的位置上。

1. $\frac{1}{9}$ 的相反数是（　　）

A、 $- \frac{1}{9}$ B、 $\frac{1}{9}$ C、-9 D、9

查看试题解析
2. “十一假期”到南宁动物园旅游人数为45000人次，数据45000用科学记数法表示为（　　）

A、45×10⁴ B、4.5×10⁴ C、4.5×10⁵ D、4.5×10⁶

查看试题解析
3. 下列各数比-3小的数是（　　）

A、0 B、1 C、-4 D、-1

查看试题解析
4. 某市某天的最高气温为8℃，最低气温为-2℃，则这天的最高气温比最低气温高（　　）

A、10℃ B、6℃ C、-6℃ D、-10℃

查看试题解析
5. 下列去括号中，正确的是（　　）

A、a²-（-4a+3）＝a²+4a+3 B、a²+（-3-4a）＝a²-3+4a C、（a-3b）-（4c-2）＝a-3b-4c+2 D、a-（c-d）＝a-c-d

查看试题解析
6. 代数式 $\frac{1}{2 x} ， - \frac{3 m n}{4} ， \frac{a + b}{2}$ ， a ， x+y ， 2023中单项式的个数有（　　）

A、3个 B、4个 C、5个 D、6个

查看试题解析
7. 下列各数-（-2），（-2）² ， -3² ，（-2）³中，负数有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 已知2x³y²和-x³^my²是同类项，则式子3m-24的值是（　　）

A、20 B、-20 C、-21 D、21

查看试题解析
9. 下列说法正确的是（　　）

A、单项式-2²xab²的次数是6 B、2x-3xy-2是一次三项式 C、单项式- $\frac{2}{3}$ πxy²的系数是- $\frac{2}{3}$ D、0是单项式

查看试题解析
10. 已知a-b＝2，c+d＝3，则（b+c）-（a-d）的值是（　　）

A、-1 B、1 C、-5 D、15

查看试题解析
11. 某同学做了一道数学题：“已知两个多项式为A、B ，且B＝2x-3y ，求A-B的值．”他误将“A-B”看成了“A+B”，结果求出的答案是x-y ，那么原来的A-B的值应该是（　　）

A、5x-3y B、3y-5x C、3x-5y D、5y-3x

查看试题解析
12. 已知a、b为有理数，下列式子：①ab＝-1；② $\frac{a}{b}$ ＜0；③| $\frac{a}{b}$ |＝- $\frac{a}{b}$ ；④|ab|＞ab ，其中一定能够确定a、b异号的有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题：本大题共6小题，每小题2分，共12分。请将答案填入答题卡相应的位置上.

13. 如果收入15元记作+15元，那么支出10元记作元．

查看试题解析
14. 比较大小：-12 -20（用“＞”“＝”或“＜”表示）．

查看试题解析
15. 用四舍五入法取近似值：4.106≈ ．（精确到百分位）

查看试题解析
16. 如图，数轴上的点P表示的数是-1，将点P移动3个单位长度得到点P'，则点P'表示的数是．

查看试题解析
17. 已知a ， b互为相反数，c ， d互为倒数，m的绝对值是2，则 $\frac{| a + b |}{2 m^{2} + 1} + 2 m - {(- c d)}^{2023}$ ＝．

查看试题解析
18. 蜜蜂是自然界神奇的“建筑师”，它能用最少的材料造成最牢固的建筑物“蜂窝”，观察下列的“蜂窝图”：

则第n个图案中的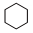个数是．（用含n的代数式表示）.

查看试题解析

三、解答题：本大题共8小题，满分共72分。将解答过程写在答题卡的相应位置上，作图或添辅助线先用铅笔画完，再用水性笔描黑。

19. 计算：-15-（-8）+（-5）．

查看试题解析
20. 计算：-3²+3÷（-1）⁴-（-4×5）．

查看试题解析
21. 先化简，再求值：2a²b-[2ab²+2（a²b-2ab²）]，其中a＝1， $b = - \frac{1}{2}$ ．

查看试题解析
22. 已知a ， b ， c在数轴上的位置如图，且|a|＜|c|．

(1)、c-a 0，abc 0，c-b 0（请用“＜”或“＞”填空）；

(2)、化简：|a-b|+|b+c|-|c-a|．

查看试题解析
23. 出租车司机某天在五一路（近似地看成一条直线）上行驶，如果规定向东为“正”，向西为“负”，他这天上午的行程可以表示为：+5，-3，+3，-10，+2，-2，+4，-5，+8，-8（单位：千米）．

(1)、司机将最后一名乘客送达目的地后需要返回出发地换班，请问司机该如何行驶才能回到出发地？

(2)、若汽车耗油量为0.8升/千米，发车前油箱有34.8升汽油，若司机将最后一名乘客送达目的地，再返回出发地，问司机今天上午是否需要加油？若要加油至少需要加多少才能返回出发地？若不用加油，请说明理由．

查看试题解析
24. 已知：A＝2x²+3xy-2x-2，B＝-x²+xy-1．

(1)、求A+B的值；

(2)、若2A+4B的值与x无关，求y的值．

查看试题解析
25. 音箱厂家生产A、B两种款式的音箱，其中每天生产A种音箱x个，两种音箱的成本和售价如表所示：

成本（元/个）
售价（元/个）
A
8
15
B
10
20

(1)、若该厂家每天生产A种音箱4000个，B种音箱2000个，求每天生产音箱的总成本；

(2)、若该厂家每天共生产音箱7500个，求每天生产音箱的总成本（用含x的式子表示）；

(3)、若该厂家每天生产B种音箱的数量是A种音箱数量的 $\frac{1}{5}$ ，则所生产的音箱全部销售完后，每天共可获利多少元？（用含x的式子表示）

查看试题解析
26. 在解决数学问题的过程中，我们常用到“分类讨论“的数学思想，下面是运用“分类讨论”的数学思想解决问题的过程，请仔细阅读，并解答问题．
【提出问题】已知有理数x ， y ， z满足xyz＞0，求 $\frac{| x |}{x} + \frac{| y |}{y} + \frac{| z |}{z}$ 的值．
【解决问题】解：由题意，得x ， y ， z三个都为正数或其中一个为正数，另两个为负数．
①当x ， y ， z都为正数，即x＞0，y＞0，z＞0时， $\frac{| x |}{x} + \frac{| y |}{y} + \frac{| z |}{z} = \frac{x}{x} + \frac{y}{y} + \frac{z}{z} = 1 + 1 + 1 = 3$ ；
②当x ， y ， z中有一个为正数，另两个为负数时，不妨设x＞0，y＜0，z＜0，则 $\frac{| x |}{x} + \frac{| y |}{y} + \frac{| z |}{z} = \frac{x}{x} + \frac{- y}{y} + \frac{- z}{z} = 1 + (- 1) + (- 1) = - 1$ ．
综上所述， $\frac{| x |}{x} + \frac{| y |}{y} + \frac{| z |}{z}$ 的值为3或-1．
【探究拓展】请根据上面的解题思路解答下面的问题：

(1)、已知x ， y是不为0的有理数，当|xy|＝-xy时， $\frac{| x |}{x} + \frac{| y |}{y}$ ＝；

(2)、已知x ， y ， z是有理数，当xyz＜0时，求 $\frac{x}{| x |} + \frac{y}{| y |} + \frac{z}{| z |}$ 的值；

(3)、已知x ， y ， z是有理数，x+y+z＝0，xyz＜0，求 $\frac{| y + z |}{x} + \frac{| x + z |}{y} + \frac{| x + y |}{z}$ 的值．

查看试题解析

	成本（元/个）	售价（元/个）
A	8	15
B	10	20