广西南宁四十七中2023-2024学年九年级上学期期中数学试卷

试卷更新日期：2023-12-24 类型：期中考试

进入出卷网下载

一、选择题（共12小题，每小题3分，共36分.在每小题给出的四个选项中只有一项是符合要求的，用2B铅笔把答题卡上对应题目的答案标号涂黑.)

1. 如果将“收入50元”记作“+50元”，那么“支出20元”记作（）

A、+20元 B、﹣20元 C、+30元 D、﹣30元

查看试题解析
2. 下列四个图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列方程中，属于一元二次方程是（）

A、2x-3＝0 B、x²+1＝ $\frac{1}{x}$ C、x²+2xy+y²＝0 D、x²-3x+2＝0

查看试题解析
4. 已知5G信号的传播速度为300000000m/s，将300000000用科学记数法表示为（）

A、3×10⁷ B、3×10⁸ C、3×10⁹ D、3×10¹⁰

查看试题解析
5. 如图，点A，B，C在⊙O上，∠AOB=72°，则∠ACB等于（）

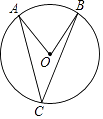A、28° B、54° C、18° D、36°

查看试题解析
6. 下列调查中，最适合采用抽样调查的是（）

A、对旅客上飞机前的安检 B、了解全班同学每周体育锻炼的时间 C、了解南宁市中学生的眼睛视力情况 D、了解某班学生的身高情况

查看试题解析
7. 把抛物线y＝x²+1先向右平移3个单位长度，再向下平移5个单位长度后，所得函数的表达式为（）

A、y＝（x+3）²-5 B、y＝（x+3）²-4 C、y＝（x-3）²+6 D、y＝（x-3）²-4

查看试题解析
8. 若点P（m，m-n）与点Q（-2，3）关于原点对称，则点M（m，n）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
9. 如图，菱形ABCD的对角线AC，BD相交于点O，AC＝12，CD＝10，则S_菱形BABCD＝（）

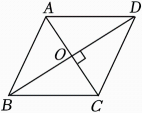A、8 B、40 C、96 D、192

查看试题解析
10. 《九章算术》中有这样一道题：今有共买羊，人出五，不足四十五；人出七，不足三，问人数、羊价几何？这道题的意思是：今有若干人共买一头羊，若每人出5钱，则还差45钱；若每人出7钱，则仍然差3钱．求买羊的人数和这头羊的价格．设买羊的人数为x人，根据题意，可列方程为（）

A、5x-45＝7x+3 B、5x+45＝7x-3 C、5x-45＝7x-3 D、5x+45＝7x+3

查看试题解析
11. 已知二次函数y＝ax²+bx+c的部分图象如图所示．有以下结论：①abc＜0；②a+c＞0：③4a+2b+c＜0；④a+b＞0．其中正确的有（）

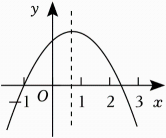A、4个 B、3个 C、2个 D、1个

查看试题解析
12. 在平面直角坐标系中，已知点A（0，1），B（0，﹣5），若在x轴正半轴上有一点C，使∠ACB＝30°，则点C的横坐标是（）

A、3 $\sqrt{3} +$ 4 $\sqrt{2}$ B、12 C、6+3 $\sqrt{3}$ D、6 $\sqrt{3}$

查看试题解析

二、填空题（本大题共6小题，每小题2分，共12分.）

13. 若分式 $\frac{1}{a}$ 在实数范围内有意义，则实数a的取值范围为．

查看试题解析
14. 分解因式：x²﹣9= .

查看试题解析
15. 关于x的方程x²-2x+k＝0有两个相等的实数根，则k的值是．

查看试题解析
16. 如图，有三条道路围成Rt△ABC，其中BC＝1000m，一个人从B处出发沿着BC行走了800m，到达D处，AD恰为∠CAB的平分线，则此时这个人到AB的最短距离为 m．

查看试题解析
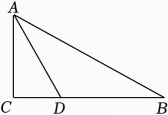17. 直线AB与⊙O相切于B点，C是⊙O与OA的交点，点D是⊙O上的动点（D与B，C不重合），若∠A＝40°，则∠BDC的度数是．

查看试题解析
18. 如图，正方形ABCD的边长为2，其面积标记为S₁ ，以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S₂ ， …按照此规律继续下去，则S₂₀₂₃的值为．

查看试题解析

三、解答题（本大题共8小题，共72分.解答应写出文字说明，证明过程或演算步骤）

19. 计算：-2²+|5-8|+ $\sqrt{16}$ +（-3）× $\frac{1}{3}$ ．

查看试题解析
20. 先化简，再求值：（2a+b）²-2a（2a-b），其中a＝-3，b＝-1．

查看试题解析
21. 如图，在平面直角坐标系xOy中，△ABC的三个顶点坐标分别为A（1，1），B（4，0），C（4，4）．

(1)、按下列要求作图：
①将△ABC向左平移4个单位，再向上平移1个单位得到△A₁B₁C₁ ．
②将△A₁B₁C₁绕点B₁逆时针旋转90°，得到△A₂B₁C₂ ．

(2)、求点C₁在旋转过程中所经过的路径长．

查看试题解析
22. 为了提高同学们的学习积极性，某校九年级举行了“数学知识竞赛”活动，并随机抽查了部分参赛同学的成绩，整理并制作图表如：
分数段
频数
频率
60≤x＜70
30
0.1
70≤x＜80
90
n
80≤x＜90
m
0.4
90≤x＜100
60
0.2
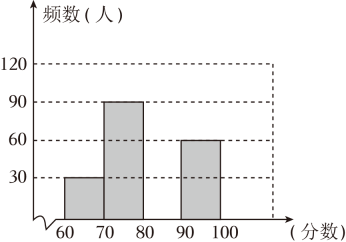
请根据图表提供的信息，解答下列问题：

(1)、请求出：m＝， n＝，抽查的总人数为人；

(2)、抽查成绩的中位数应落在分数段内；

(3)、若满分人数有甲、乙、丙、丁四人，现决定从这四名同学中任选两名参加市里的决赛，求恰好选中甲、乙两位同学的概率．（用树状图或列表法解答）

查看试题解析
23. 如图，AB为⊙O的直径，C、D为⊙O上的两个点， $\overset{⌢}{AC}$ ＝ $\overset{⌢}{C D}$ ＝ $\overset{⌢}{D B}$ ，连接AD ，过点D作DE⊥AC交AC的延长线于点E ．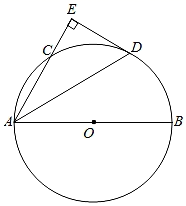

(1)、求证：DE是⊙O的切线．

(2)、若直径AB＝6，求AD的长．

查看试题解析
24. 某宾馆有50个房间可供游客居住，当每个房间每天的定价为180元时，房间会全部住满，当每个房间每天的定价增加10元时，就会有一个房间空闲，如果游客居住房间，宾馆需对每个房间每天支出20元的各种费用，设每个房间的定价增加x元（x为10的整数倍），此时入住的房间数为y间，宾馆每天的利润为w元．

(1)、直接写出y（间）与x（元）之间的函数关系；

(2)、如何定价才能使宾馆每天的利润w（元）最大？

(3)、若宾馆每天的利润为10800元，则每个房间每天的定价为多少元？

查看试题解析
25. 阅读理解：已知三角形的中线具有等分三角形面积的性质，即如图①，AD是△ABC中BC边上的中线，则S_△ABD＝S_△ACD＝ $\frac{1}{2}$ S_△AB_C ，理由：∵BD＝CD，∴S_△ABD＝ $\frac{1}{2}$ BD，AH＝ $\frac{1}{2}$ CD·AH= S_△ACD₌ $\frac{1}{2}$ S_△AB_C ，即：等底同高的三角形面积相等．
回答下列问题：

(1)、如图②，点A、B、C分别是CE、AF、BD的中点，且S_△ABC＝2，则图②中阴影部分的面积为；

(2)、如图③，已知四边形ABCD的面积是m，E、F、G、H分别是AB、BC、CD、DA的中点，点P是四边形ABCD内一点，求出图中阴影部分的面积．

查看试题解析
26. 如图，抛物线y＝ax²+4x+c经过原点O（0，0）和点A（3，3），P为抛物线上的一个动点，过点P作x轴的垂线，垂足为B（m，0），并与直线OA交于点C．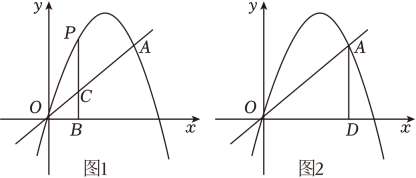

(1)、求抛物线的解析式；

(2)、当点P在直线OA上方时，求线段PC的最大值；

(3)、过点A作AD⊥x轴于点D，在抛物线上是否存在点P，使得以P、A、C、D四点为顶点的四边形是平行四边形？若存在，求m的值；若不存在，请说明理由．

查看试题解析

分数段	频数	频率
60≤x＜70	30	0.1
70≤x＜80	90	n
80≤x＜90	m	0.4
90≤x＜100	60	0.2