广西桂林市临桂区2023-2024学年八年级上学期期中数学试卷

试卷更新日期：2023-12-24 类型：期中考试

进入出卷网下载

一、选择题（共12小题，每小题3分，共36分）

1. 下列各式为分式的是（　　）

A、x-1 B、 $\frac{1}{x}$ C、x D、 $\frac{x}{2}$

查看试题解析
2. 要使分式 $\frac{1}{x + 2}$ 的值存在，则x满足的条件是（　　）

A、x＝-2 B、x≠2 C、x＞-2 D、x≠-2

查看试题解析
3. 一个三角形的两边长分别是2和3，若它的第三边长为奇数，则这个三角形的周长为（　　）

A、3 B、5 C、7 D、8

查看试题解析
4. 小时候我们用肥皂水吹泡泡，其泡沫的厚度约0.000326毫米，用科学记数法表示为（　　）

A、3.26×10^﹣⁴毫米 B、0.326×10^﹣⁴毫米 C、3.26×10^﹣⁴厘米 D、32.6×10^﹣⁴厘米

查看试题解析
5. 已知等腰三角形的一个内角为70°，则另两个内角的度数是（）

A、55°，55° B、70°，40° C、55°，55°或70°，40° D、以上都不对

查看试题解析
6. 一个等腰三角形两边的长分别为4和9，那么这个三角形的周长是（）

A、13 B、17 C、22 D、17或22

查看试题解析
7. 下列运算正确的是（）

A、x³•x³＝x⁹ B、x⁸÷x⁴＝x² C、（ab³）²＝ab⁶ D、（2x）³＝8x³

查看试题解析
8. 为了践行“绿色生活”的理念，甲、乙两人每天骑自行车出行，甲匀速骑行30公里的时间与乙匀速骑行25公里的时间相同，已知甲每小时比乙多骑行2公里，设甲每小时骑行x公里，根据题意列出的方程正确的是（　　）

A、 $\frac{25}{x} = \frac{30}{x + 2}$ B、 $\frac{25}{x - 2} = \frac{30}{x}$ C、 $\frac{25}{x} = \frac{30}{x - 2}$ D、 $\frac{25}{x + 2} = \frac{30}{x}$

查看试题解析
9. 如图，点A、B、C表示某公司三个车间的位置，现在要建一个仓库，要求它到三个车间的距离相等，则仓库应建在（　　）

A、△ABC三边的中线的交点上 B、△ABC三内角平分线线交点上 C、△ABC三条边高的交点上 D、△ABC三边垂直平分线的交点上

查看试题解析
10. 若分式 $\frac{x^{2} - 4}{x + 2}$ 的值为0，则x的值为（）

A、﹣2 B、0 C、2 D、±2

查看试题解析
11. 如图，在△ABC中，已知点D ， E ， F分别为边BC，AD ， CE的中点，S_△_ABC＝8cm² ，则阴影部分的面积（　　）

A、4 B、2 C、1 D、 $\frac{1}{2}$

查看试题解析
12. 如图，在△ABC中，点D为BC边的中点，点E为AC上一点，将∠C沿DE翻折，使点C落在AB上的点F处，若∠A=55°，∠AEF的度数为（　　）

A、70° B、40° C、75° D、50°

查看试题解析

二、填空题（共6小题，每小题2分，共12分）

13. $\frac{2 x}{3 y} = \frac{()}{3 x y}$ ．

查看试题解析
14. 若解分式方程 $\frac{x - 1}{x + 4} = \frac{m}{x + 4}$ 产生增根，则m= ．

查看试题解析
15. 分式 $\frac{3}{4 a^{2} b} 与 \frac{1}{a b^{2} c}$ 的最简公分母是．

查看试题解析
16. 已知，如图：∠ABC＝∠DEF ， BE＝CF ，要说明△ABC≌△DEF，若以“SAS”为依据，还要添加的条件为．

查看试题解析
17. 如图，在等腰三角形ABC中，AB＝AC ， DE垂直平分AB，已知∠ADE＝40°，则∠DBC＝°．

查看试题解析
18. 如图，在△ABC中，∠B＝40°，三角形的外角∠DAC和∠ACF的平分线交于点E，则∠AEC＝．

查看试题解析

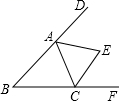
三、解答题（本大题共8题，共72分，请将答案写在答题卡上）.

19. 计算：|-4|+（-1）²⁰²³×（π-3.14）⁰+（- $\frac{1}{2}$ ）^-1 ．

查看试题解析
20. 解方程： $\frac{x - 3}{x - 2} + 1 = \frac{3}{2 - x}$ ．

查看试题解析
21. 先化简分式 $\frac{a^{2} - 1}{a^{2} + 2 a + 1} \div \frac{a^{2} - a}{a + 1}$ ，然后请你选取一个合适的a值代入，求分式的值．

查看试题解析
22. 如图，△ABD≌△EBC ， AB＝2cm，BC=5cm

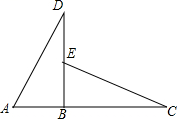(1)、求DE的长；

(2)、若A、B、C在一条直线上，则DB与AC垂直吗？为什么？

查看试题解析
23. 如图，在△ABC中，BD平分∠ABC ，

(1)、作图：作BC边的垂直平分线分别交BC ， BD于点E ， F（用尺规作图法，保留作图痕迹，不要求写作法）；

(2)、在（1）的条件下，连接CF ，若∠A=60°，∠ABD＝24°，求∠ACF的度数．

查看试题解析
24. 某文化用品商店用1000元购进一批“晨光”套尺，很快销售一空；商店又用1500元购进第二批该款套尺，购进时单价是第一批的 $\frac{5}{4}$ 倍，所购数量比第一批多100套．

(1)、求第一批套尺购进时单价是多少？

(2)、若商店以每套4元的价格将这两批套尺全部售出，可以盈利多少元？

查看试题解析
25. 如图：在△ABC中，BE、CF分别是AC、AB两边上的高，在BE上截取BD＝AC ，在CF的延长线截取CG=AB，连接AD、AG ．

(1)、求证：AD＝AG；

(2)、AD与AG的位置关系如何，请说明理由．

查看试题解析
26. 数学模型学习与应用：
白日登山望峰火，黄昏饮马傍交河．——《古从军行》唐李欣
模型学习：诗中隐含着一个有趣的数学问题，我们称之为“将军饮马”问题．关键是利用轴对称变换，把直线同侧两点的折线问题转化为直线两侧的线段问题，从而解决距离和最短的一类问题，“将军饮马”问题的数学模型如图1所示：在直线l上存在点P ，使PA+PB的值最小．
作法：作A点关于直线l的对称点A'，连接A'B ， A'B与直线l的交点即为点P ．此时PA+PB的值最小．

(1)、模型应用：
如图2，已知△ABC为等边三角形，高AH＝8cm ， P为AH上一动点，D为AB的中点．
①当PD+PB的最小值时，在图中确定点P的位置（要有必要的画图痕迹，不用写画法）．
②则PD+PB的最小值为 ▲ cm ．

(2)、模型变式：
如图3所示，某地有块三角形空地AOB ，已知∠AOB＝30°，P是△AOB内一点，连接PO后测得PO＝10米，现当地政府欲在三角形空地AOB中修一个三角形花坛PQR ， 点Q、R分别是OA ， OB边上的任意一点（不与各边顶点重合），求△PQR周长的最小值.

查看试题解析