广东省佛山市三水区九校联考2023-2024学年八年级上学期数学期中试卷

试卷更新日期：2023-12-23 类型：期中考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. $9$ 的平方根是（）

A、 $- 3$ B、 $3$ C、 $\pm 3$ D、 $81$

查看试题解析
2. 下列各数中，是无理数的是（）

A、 $- 2$ B、 $- π$ C、 $\sqrt{16}$ D、 $\frac{1}{7}$

查看试题解析
3. 下列二次根式中，属于最简二次根式的是（）

A、 $\sqrt{7}$ B、 $\sqrt{12}$ C、 $\sqrt{8}$ D、 $\sqrt{1.5}$

查看试题解析
4. 在平面直角坐标系中，点P $(3 ， - 1)$ 关于y轴的对称点的坐标是（）

A、 $(- 1 ， 3)$ B、 $(- 3 ， 1)$ C、 $(3 ， 1)$ D、 $(- 3 ， - 1)$

查看试题解析
5. 下列计算正确的是（　　）

A、 $\sqrt{12} - \sqrt{3} = \sqrt{3}$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $3 \sqrt{5} \times \sqrt{5} = 4 \sqrt{5}$ D、 $(2 \sqrt{2})^{2} = 4 \sqrt{2}$

查看试题解析
6. 估计 $\sqrt{13}$ 的值在（）

A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间

查看试题解析
7. 一个直角三角形的两直角边长分别为5和12，则它斜边上的高长为（）

A、13 B、 $\frac{13}{2}$ C、 $\frac{60}{13}$ D、 $\frac{12}{5}$

查看试题解析
8. 点P在第二象限，且到y轴的距离为3，到x轴的距离为5，则P点的坐标是（）

A、（3，－5） B、（5，－3） C、（－3，5） D、（－5，3）

查看试题解析
9. 如图，在 $4 \times 4$ 的网格中，每个小正方形的边长均为1，点A、B都在格点上，则下列结论错误的是（）

A、 $△ A B C$ 的面积为10 B、 $∠ B A C = 90 °$ C、 $A B = 2 \sqrt{5}$ D、点A到直线 $B C$ 的距离是2

查看试题解析
10. 如图，已知四边形ABCD的顶点为 $A (1 ， 2)$ ， $B (- 1 ， 2)$ ， $C (- 1 ， - 2)$ ， $D (1 ， - 2)$ ，点M和点N同时从点 $E (0 ， 2)$ 出发作顺时针运动，点M的速度为1个单位每秒，点N的速度为4个单位每秒，那么点N第2024次追上点M时的坐标为（）

A、 $(1 ， - 1)$ B、 $(- 1 ， - 1)$ C、 $(0 ， 2)$ D、 $(- 1 ， 1)$

查看试题解析

二、填空题（每题3分，共18分）

11. 若代数式 $\sqrt{x - 1}$ 有意义，则实数x 的取值范围是.

查看试题解析
12. 如图，数字代表所在正方形的面积，则A所代表的正方形的面积为.

查看试题解析
13. 比较大小：5 $2 \sqrt{5}$ （填“ $<$ ”、“＝”或“ $>$ ”）．

查看试题解析
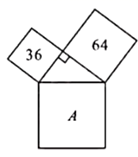14. 如果点 $P (- 2 ， b)$ 和点 $Q (a ， - 3)$ 关于x轴对称，那么a-b的值是．

查看试题解析
15. 若有一个数m ，它的平方根是a+1和2a-7，则m为．

查看试题解析
16. 如图，点 $A (1 ， 0) ， B (2 ， 3)$ 在x轴上找一点P ，使 $△ P A B$ 是等腰三角形，则满足条件的P点坐标是．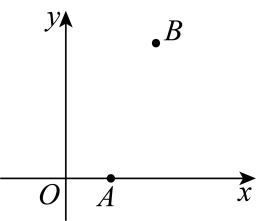

查看试题解析

三、解答题（17-20题每题6分，21-23每题8分，24-25每题12分）

17.

(1)、计算： $\frac{\sqrt{6} \times \sqrt{3}}{\sqrt{2}}$ ；

(2)、计算： $(\sqrt{27} - \sqrt{\frac{1}{3}}) \times \sqrt{3}$

查看试题解析
18. 计算 $\sqrt{\frac{3}{2}} - \sqrt{24} + \sqrt{\frac{6}{5}} \times \sqrt{45}$ ．

查看试题解析
19. 已知 $\sqrt{a + 2} + | b - 1 | = 0$ ，求 ${(a + b)}^{2023}$ 的值．

查看试题解析
20. 如图，在平面直角坐标系中， $△ A B C$ 的三个顶点的坐标分别为 $A (- 2 ， 4) ， B (- 4 ， 1) ， C (- 1 ， 2)$ ．

(1)、作出 $△ A B C$ 关于y轴对称的 $△ A_{1} B_{1} C_{1}$ ，并写出点 $A_{1}$ 的坐标；

(2)、求 $△ A B C$ 的面积．

查看试题解析
21. 已知 $2 a - 1$ 的平方根是 $\pm 3$ ， $2 a - b$ 的立方根是 $2$ ，求 $a + 2 b$ 的平方根

查看试题解析
22. 已知：在四边形ABCD中，∠ACB=90°，AB=15，BC=9，AD=5，CD=13.

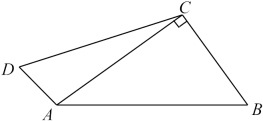(1)、求 $A C$ 的长．

(2)、 $△ A C D$ 是直角三角形吗？如果是，请说明理由．

(3)、求这块空地的面积．

查看试题解析
23. 小宇手里有一张直角三角形纸片 $A B C$ ，他无意中将直角边AC折叠了一下，恰好使 $A C$ 落在斜边 $A E$ 上，且C点与E点重合，（如图）小宇经过测量得知两直角边 $A C = 6$ ， $B C = 8$ ．他想用所学知识求出CD的长.

(1)、 $A B =$ ； $A E =$ ； $B E =$ ；

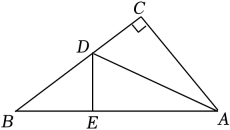(2)、设 $C D$ 为 $x$ ，则 $B D$ 可用 $x$ 表示为；

(3)、利用以上结论求出 $C D$ 的长．

查看试题解析
24. 已知：如图，有一块 $R t △ A B C$ 的绿地，量得两直角边 $A C = 8$ m， $B C = 6 m$ ，现要将这块绿地扩充成等腰 $△ A B D$ ，且扩充部分（ $△ A D C$ ）是以8m为直角边长的直角三角形，求扩充后等腰△ABD的周长.

(1)、在图1中，当 $A B = A D = 10$ m时， $△ A B D$ 的周长为；

(2)、在图2中，当 $B A = B D = 10$ m时， $△ A B D$ 的周长为；

(3)、在图3中，当 $D A = D B$ 时，求 $△ A B D$ 的周长．

查看试题解析
25. 综合与实践．

(1)、积累经验
我们在第十二章《全等三角形》中学习了全等三角形的性质和判定，在一些探究题中经常用以上知识转化角和边，进而解决问题．例如：我们在解决：“如图1，在△ABC中， $∠ A C B ＝ 90 °$ ， $A C ＝ B C$ ，线段DE经过点C，且 $A D ⊥ D E$ 于点D ， $B E ⊥ D E$ 于点E ．求证： $A D ＝ C E$ ，只要证明 $△ A D C ≌ △ C E B$ ，即可得到解决；

(2)、类比应用
如图2，在平面直角坐标系中， $△ A B C$ 中，∠ACB=90°， $A C ＝ B C$ ，点A的坐标为 $(0 ， 2) ，$ 点C的坐标为 $(1 ， 0)$ ，求点B的坐标．

(3)、拓展提升
如图3， $△ A B C$ 在平面直角坐标系中， $∠ A C B ＝ 90 °$ ， AC=BC，点A的坐标为 $(2 ， 1)$ ，点C的坐标为 $(4 ， 2)$ ，则点B坐标为．

查看试题解析