广西南宁市江南区2023-2024学年上学期七年级期中数学试卷

试卷更新日期：2023-12-23 类型：期中考试

进入出卷网下载

一、选择题（共12小题，每小题3分，共36分，在每小题给出的四个选项中只有一项是

1. 2023的倒数是（）

A、2023 B、-2023 C、 $- \frac{1}{2023}$ D、 $\frac{1}{2023}$

查看试题解析
2. 多项式3xy-5x²y+4的常数项为（）

A、3 B、-5 C、4 D、-4

查看试题解析
3. 第19届亚运会将于2023年9月23日在杭州举行，其主体育场及田径项目比赛场地——杭州奥体中心体育场，俗称“大莲花”，总建筑面积约216000平方米，将数216000用科学记数法表示为（）

A、216×10³ B、21.6×10⁴ C、2.16×10⁵ D、0.216×10⁶

查看试题解析
4. 下列代数式3，a+1，a，1-y，3x中，单项式共有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
5. 下列各组数中，互为相反数的是（）

A、 $- \frac{1}{3}$ 和-3 B、-2和2 C、-3.5和5.3 D、 $\frac{3}{5}$ 和 $\frac{5}{3}$

查看试题解析
6. 下列计算正确的是（）

A、4a-2a＝2a B、5a³-3a²＝2a C、5a+2b＝7ab D、y²+2y²＝3y⁴

查看试题解析
7. 气温由-2℃上升3℃后是（）

A、-5℃ B、1℃ C、5℃ D、3℃

查看试题解析
8. 下列多项式中，属于三次二项式的是（）

A、3a-2 B、a²-c C、1-2x³ D、x³-2y+1

查看试题解析
9. 用四舍五入法对有理数1.688取近似数，其中正确的是（）

A、1.6（精确到十分位） B、1（精确到个位） C、1.68（精确到0.01） D、1.7（精确到0.1）

查看试题解析
10. 下列去括号正确的是（）

A、+（a-b）＝a+b B、+（a-b）＝-a+b C、-（a-b）＝-a-b D、-（a-b）＝-a+b

查看试题解析
11. 已知数a，b在数轴上表示的点的位置如图所示，则下列结论正确的是（）

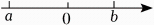A、a+b＞0 B、a-b＞0 C、a•b＞0 D、-a＞-b

查看试题解析
12. 一个两位数，十位上的数为a，个位上的数为b，若把这个两位数的十位上的数和个位上的数交换位置，计算所得的数和原数的和，用a，b可以表示为（）

A、11a+11b B、11ab C、10a+10b D、10ab

查看试题解析

二、填空题（本大题共6小题，每小题2分，共12分）

13. |-4|＝．

查看试题解析
14. 单项式-3xy²次数是．

查看试题解析
15. 比较大小：-3 -5．（用符号＞、＜、＝填空）

查看试题解析
16. 如果单项式x²y³与2x²y^b是同类项，那么b＝．

查看试题解析
17. 某种商品原价是每件a元，商店老板为了增加销量，减少库存，第一次降价打“八折”，第二次降价每一件又减8元．两次降价后的每件售价是元．

查看试题解析
18. 如图，A点的初始位置位于数轴上表示1的点，现对A点做如下移动：第1次向左移动3个单位长度至B点，第2次从B点向右移动6个单位长度至C点，第3次从C点向左移动9个单位长度至D点，第4次从D点向右移动12个单位长度至E点，…，依此类推，这样第次移动到的点到原点的距离为2023．

查看试题解析

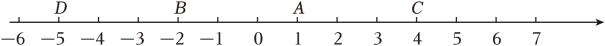
三、解答题（本大题共8小题，共72分，解答应写出文字说明、证明过程或演算步骤，）

19. 计算：-1³+3×（-2）²-8÷2．

查看试题解析
20. 先化简，再求值：2（3a²b+ab）-（ab+6a²b），其中a＝-1，b＝2．

查看试题解析
21. 画出数轴，在数轴上表示下列各数，并按从小到大用“＜”把这些数连接起来．
3.5，-2，0，-1.6， $- \frac{1}{3}$ ， $\frac{3}{2}$ ．

查看试题解析
22. 在“老城换新颜”小区改造中，为了提高居民的宜居环境，某小区规划修建一个广场（平面图形如图阴影部分所示）．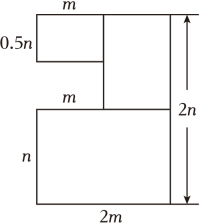

(1)、用含m，n的代数式表示广场（阴影部分）的面积S；

(2)、若m＝12米，n＝20米，修建每平方米需费用20元，求出修建该广场的总费用．

查看试题解析
23. 若a、b互为相反数，c、d互为倒数，m的绝对值为2.

(1)、直接写出a＋b ， cd ， m的值；

(2)、求m＋cd＋ $\frac{a + b}{m}$ 的值．

查看试题解析

24. 某校七年级（1）班学生在劳动课上采摘成熟的白萝卜，一共采摘了9筐，以每筐25千克为标准，超过的千克数记作正数，不足的千克数记作负数，称重后记录如下：

（1）	（2）	（3）	（4）	（5）	（6）	（7）	（8）	（9）

-2.5	1.5	-3	2	-0.5	1	-2	-2	-2.5

回答下面问题：

(1)、这9筐白萝卜，最接近25千克的这筐白萝卜实际质量为千克．

(2)、以每筐25千克为标准，这9筐白萝卜总计超过或不足多少千克？

(3)、若白萝卜每千克售价2元，则售出这9筐白萝卜可得多少元？

查看试题解析

25. 某商场电器销售一种微波炉和电磁炉，微波炉每台定价500元，电磁炉每台定价200元．“双11”期间商场决定开展促销活动，活动期间向客户提供两种优惠方案．
方案一：买一台微波炉送一台电磁炉；
方案二：微波炉和电磁炉都按定价的80%付款．现某客户要到该卖场购买微波炉10台，电磁炉x台（x＞10）．

(1)、若该客户按方案一购买，需付款多少元．（用含x的代数式表示）；
若该客户按方案二购买，需付款多少元．（用含x的代数式表示）

(2)、若x＝30，通过计算说明此时按哪种方案购买较为合算？

(3)、当x＝30时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法．

查看试题解析
26. 在解决数学问题的过程中，我们常用到“分类讨论”的数学思想，下面是运用分类讨论思想解决问题的过程，请仔细阅读，并解答问题．
⑴[提出问题]三个有理数a，b，c满足abc＞0，求 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值．
⑵[解决问题]由题意，得a，b，c三个有理数都为正数或其中一个为正数，另外两个为负数．
①a，b，c都是正数，即a＞0，b＞0，c＞0时，则 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ = $\frac{a}{a} + \frac{b}{b} + \frac{c}{c}$ ＝1+1+1＝3；
②当a，b，c中有一个为正数，另外两个为负数时，不妨设a＞0，b＜0，c＜0，则 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ ＝ $\frac{- a}{a} + \frac{- b}{b} + \frac{- c}{c}$ ＝1+（-1）+（-1）＝-1．
综上所述， $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值为3或-1．
⑶[探究拓展]请根据上面的解题思路解答下面的问题：

(1)、已知a，b是不为0的有理数，当|ab|＝-ab时，则 $\frac{| a |}{a} + \frac{| b |}{b}$ 的值是；

(2)、已知a，b，c是有理数，当abc＜0时，求 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值；

(3)、已知a，b，c是有理数，a+b+c＝0，abc＜0，求 $\frac{b + c}{| a |} + \frac{c + a}{| b |} + \frac{a + b}{| c |}$ 的值．

查看试题解析