广西南宁市部分校联考2023-2024学年九年级上学期9月份月考数学试卷

试卷更新日期：2023-12-23 类型：月考试卷

进入出卷网下载

一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）

1. 我们生活在一个充满对称的世界中，生活中的轴对称图形随处可见，下面几幅图片是校园中运动场上代表体育项目的图标，其中可以看作是轴对称图形的是（）

A、乒乓球 B、跳远 C、举重 D、武术

查看试题解析
2. 下列方程中，属于一元二次方程的是（）

A、 $x - 2 y = 1$ B、 $x^{2} + 3 = \frac{2}{x}$ C、 $x^{2} - 2 y + 4 = 0$ D、 $x^{2} - 2 x + 1 = 0$

查看试题解析
3. 以下调查中，最适合用来全面调查的是（）

A、调查柳江流域水质情况 B、了解全国中学生的心理健康状况 C、了解全班学生的身高情况 D、调查春节联欢晚会收视率

查看试题解析
4. 将方程 $x^{2} - 8 x = 10$ 化为一元二次方程的一般形式，其中二次项系数为 $1$ ，一次项系数、常数项分别是（）

A、 $- 8$ 、 $- 10$ B、 $- 8$ 、 $10$ C、 $8$ 、 $- 10$ D、 $8$ 、 $10$

查看试题解析
5. 关于二次函数 $y = 2 {(x - 4)}^{2} + 6$ 的最大值或最小值，下列说法正确的是（）

A、有最大值4 B、有最小值4 C、有最大值6 D、有最小值6

查看试题解析
6. 把函数 $y = 2 x^{2}$ 的图象向下平移 $2$ 个单位长度得到新图象，则新函数的表达式是（）

A、 $y = 2 (x - 2)^{2}$ B、 $y = 2 (x + 2)^{2}$ C、 $y = 2 x^{2} + 2$ D、 $y = 2 x^{2} - 2$

查看试题解析
7. 抛物线 $y = a (x + 1)^{2} + 2$ 的一部分如图所示，该抛物线在 $y$ 轴右侧部分与 $x$ 轴交点的坐标是（）

A、 $(\frac{1}{2} ， 0)$ B、 $(1 ， 0)$ C、 $(2 ， 0)$ D、 $(3 ， 0)$

查看试题解析
8. 一元二次方程 $2 x^{2} - m x + 3 = 0$ 的一根为 $3$ ，则 $m$ 的值为（）

A、 $7$ B、 $5$ C、 $- 7$ D、 $- 5$

查看试题解析
9. 从地面竖直向上抛出一小球，小球的高度 $h ($ 单位： $m)$ 与小球的运动时间 $t ($ 单位： $s)$ 之间的关系式是 $h = 30 t - 5 t^{2}$ ，小球运动到最高点所需的时间是（）

A、 $2 s$ B、 $3 s$ C、 $4 s$ D、 $5 s$

查看试题解析
10. 在“双减政策”的推动下，某初级中学校学生课后作业时长明显减少 $. 2021$ 年上学期每天作业平均时长为 $100 m i n$ ，经过 $2021$ 年下学期和 $2022$ 年上学期两次调整后， $2022$ 年下学期平均每天作业时长为 $70 m i n .$ 设该校平均每天作业时长这两学期每期的下降率为 $x$ ，则可列方程为（）

A、 $100 (1 - x^{2}) = 70$ B、 $70 (1 + x^{2}) = 100$ C、 $100 (1 - x)^{2} = 70$ D、 $70 (1 + x)^{2} = 100$

查看试题解析
11. 二次函数 $y = {(x - \frac{3}{2})}^{2} + \frac{3}{4}$ 的图象 $(1 \leq x \leq 3)$ 如图所示，则该函数在所给自变量的取值范围内，函数值y的取值范围是（）

A、 $y \geq 1$ B、 $1 \leq y \leq 3$ C、 $\frac{3}{4} \leq y \leq 3$ D、 $0 \leq y \leq 3$

查看试题解析
12. 如图所示，将边长为 $12 c m$ 的正方形 $A B C D$ 沿其对角线 $A C$ 剪开，再把 $△ A B C$ 沿着 $A D$ 方向平移得到 $△ A' B' C'$ ，若两个三角形重叠部分的面积为 $32 c m^{2}$ ，则它移动的距离 $A A'$ 等于（）

A、 $4 c m$ B、 $6 c m$ C、 $8 c m$ D、 $4 c m$ 或 $8 c m$

查看试题解析

二、填空题（本大题共6小题，共12.0分）

13. 若 $\sqrt{x - 2}$ 在实数范围内有意义，则实数x的取值范围是．

查看试题解析
14. 若点 $A (- 1 ， y_{1})$ ， $B (2 ， y_{2})$ 在抛物线． $y = 2 x^{2}$ 上，则 $y_{1}$ ， $y_{2}$ 的大小关系为： $y_{1}$ $y_{2} . ($ 选填“ $>$ ”“ $<$ 或“ $=$ ” $)$

查看试题解析
15. 关于x的一元二次方程x²+2x+m=0有两个相等的实数根，则m的值是．

查看试题解析
16. 如图，在菱形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点 $O$ ， $B D = 8$ ， $A C = 6$ ， $O E / / A B$ ，交 $B C$ 于点 $E$ ，则 $O E$ 的长为．

查看试题解析
17. 已知等腰三角形的底边长为 $7$ ，腰长是 $x^{2} - 8 x + 15 = 0$ 的一个根，则这个三角形周长为．

查看试题解析
18. 已知实数 $a \geq 0$ ， $b \geq 0$ ，且 $a + b = 4$ ，记代数式 $w = a^{2} + a b + b^{2}$ ，记 $w_{1}$ ， $w_{2}$ 分别为代数式 $w$ 的最大值与最小值，则 $w_{1} - w_{2}$ 的值为．

查看试题解析

三、解答题（本大题共8小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）

19. 计算： $(- 1)^{0} - \sqrt{9} + (- 2)^{2} + | - 2 |$ ．

查看试题解析
20. 用配方法解方程： $x^{2} - 6 x + 8 = 0$

查看试题解析
21. 2023年4月24日中国航天日主场活动暨中国航天大会在合肥市开幕，今年中国航天日的主题是“格物致知，叩问苍穹”.某学校为了解八年级学生对航空航天知识的了解情况，组织了一次知识竞赛活动，从两班各随机抽取了10名学生的成绩，整理如下：（成绩得分用 $x$ 表示，共分成四组：A. $80 \leq x < 85$ ， B. $85 \leq x < 90$ ， C. $90 \leq x < 95$ ， D. $95 \leq x \leq 100$ ）
八年级（1）班10名学生的成绩是：96，80，96，86，99，98，92，100，89，84.
八年级（2）班10名学生的成绩在C组中的数据是：94，90，92.
通过数据分析，列表如下：
八年级（1）班、（2）班抽取的学生竞赛成绩统计表

班级
平均数
中位数
众数
方差
八年级（1）班
92
          $b$
          $c$
43.4
八年级（2）班
92
93
100
50.4
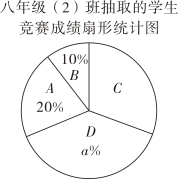
根据以上信息，解答下列问题：

(1)、填空： $a =$ ， $b =$ ， $c =$ ；

(2)、学校欲选派成绩比较稳定的班级参加下一阶段的活动，根据表格中的数据，学校会选派哪一个班级?请说明理由；

(3)、已知八年级两个班共120人参加了此次竞赛活动，估计两班参加此次竞赛活动成绩优秀 $(x \geq 90)$ 的学生总人数是多少?

查看试题解析
22. 已知二次函数 $y = x^{2} - 4$ 的图象与 $x$ 轴交于 $A$ 、 $B$ 两点 $(A$ 在 $B$ 左侧 $)$ ，与 $y$ 轴交于 $C$ 点．

(1)、0分别写出 $A$ 、 $B$ 、 $C$ 三点坐标： $A$ ， $B$ ， $C$ ；

(2)、在所给的平面直角坐标系中画出该函数图象示意图；

(3)、任写出两条该函数图象具备的特征：① ；② ．

查看试题解析
23. 在平面直角坐标系中，抛物线 $y = a x (x - 6) + 1 (a \neq 0)$ 的顶点为 $A$ ．

(1)、判断点 $(0 ， 1)$ 是否在抛物线 $y = a x (x - 6) + 1 (a \neq 0)$ 上，并说明理由；

(2)、若点 $A$ 到 $x$ 轴的距离为5，求 $a$ 的值．

查看试题解析
24. 甲、乙两工程队合作完成某修路工程，该工程总长为4800米，原计划32小时完成．甲工程队每小时修路里程比乙工程队的2倍多30米，刚好按时完成任务．

(1)、求甲工程队每小时修的路面长度；

(2)、通过勘察，地下发现大型溶洞，此工程的实际施工里程比最初的4800米多了1000米，在实际施工中，乙工程队修路效率保持不变的情况下，时间比原计划增加了( $m + 25$ )小时；甲工程队的修路速度比原计划每小时下降了 $3 m$ 米，而修路时间比原计划增加m小时，求m的值．

查看试题解析
25. 综合与实践
综合实践课上，老师让同学们以“三角形纸片的折叠”为主题开展数学活动．

(1)、【操作发现】对折 $△ A B C (A B > A C)$ ，使点 $C$ 落在边 $A B$ 上的点 $E$ 处，得到折痕 $A D$ ，把纸片展平，如图 $1 .$ 小明根据以上操作发现：四边形 $A E D C$ 满足 $A E = A C$ ， $D E = D C .$ 查阅相关资料得知，像这样的有两组邻边分别相等的四边形叫作“筝形” $.$ 请写出图 $1$ 中筝形 $A E D C$ 的一条性质．

(2)、【探究证明】如图 $2$ ，连接 $E C$ ，设筝形 $A E D C$ 的面积为 $S .$ 若 $A D + E C = 12$ ，求 $S$ 的最大值；

(3)、【迁移应用】在 $R t △ A B C$ 中， $∠ A = 90 °$ ， $A B = 2$ ， $A C = 1$ ，点 $D$ ， $E$ 分别在 $B C$ ， $A B$ 上，当四边形 $A E D C$ 是筝形时，请直接写出四边形 $A E D C$ 的面积．

查看试题解析
26. 如图，在平面直角坐标系中，直线 $A B$ 和抛物线交于点 $A (- 4 ， 0)$ ， $B (0 ， 4)$ ，且抛物线的对称轴为直线 $x = - 1$ ．

(1)、求抛物线的解析式；

(2)、点 $N$ 在第四象限的抛物线上，且 $△ N A B$ 是以 $A B$ 为底的等腰三角形，求 $N$ 点的坐标；

(3)、点 $P$ 是直线 $A B$ 上方抛物线上的一动点，当点 $P$ 在何处时，点 $P$ 到直线 $A B$ 的距离最大，并求出最大距离．

查看试题解析

班级	平均数	中位数	众数	方差
八年级（1）班	92	$b$	$c$	43.4
八年级（2）班	92	93	100	50.4