人教A版高一(上)数学期末突击训练专题:第五章(选择题)
试卷更新日期:2023-12-22 类型:复习试卷
一、选择题
-
1. 如图是杭州2023年第19届亚运会会徽,名为“潮涌”,主体图形由扇面、钱塘江、钱江潮头、赛道、互联网符号及象征亚奥理事会的太阳图形六个元素组成,集古典美和现代美于一体,富有东方神韵和时代气息。其中扇面的圆心角为 , 从里到外半径以1递增,若这些扇形的弧长之和为(扇形视为连续弧长,中间没有断开),则最小扇形的半径为( )
 A、6 B、8 C、9 D、122. 已知 为正方体 表面上的一个动点, 是棱 延长线上一点,且 ,若 ,则动点 的运动轨迹的长为( )A、 B、 C、 D、3. 在平面直角坐标系xOy中,以原点O为圆心的单位圆与锐角x的终边交于点P,过点作x轴的垂线与锐角x的终边交于点T,如图所示,的面积小于扇形AOP的面积,扇形AOP的面积小于的面积,则( )
A、6 B、8 C、9 D、122. 已知 为正方体 表面上的一个动点, 是棱 延长线上一点,且 ,若 ,则动点 的运动轨迹的长为( )A、 B、 C、 D、3. 在平面直角坐标系xOy中,以原点O为圆心的单位圆与锐角x的终边交于点P,过点作x轴的垂线与锐角x的终边交于点T,如图所示,的面积小于扇形AOP的面积,扇形AOP的面积小于的面积,则( ) A、 , B、 , C、 , D、 ,4. 如图,以棱长为2的正方体的顶点A为球心,以 为半径做一个球面,则该正方体的表面被球面所截得的所有弧长之和为( ).
A、 , B、 , C、 , D、 ,4. 如图,以棱长为2的正方体的顶点A为球心,以 为半径做一个球面,则该正方体的表面被球面所截得的所有弧长之和为( ). A、 B、 C、 D、5. 已知实数 , 满足 , 则的最小值为( )A、 B、 C、 D、6. 在数学史上,为了三角计算的简便并追求计算的精确性,曾经出现过下列两种三角函数:定义 为角 的正矢,记作 ;定义 为角 的余矢,记作 .则下列说法正确的是( )A、 B、若 ,则 C、函数 在 上单调递增 D、函数 的最小值为7. 《周髀算经》中给出的弦图是由四个全等的直角三角形和中间一个小正方形拼成的一个大的正方形,若图中所示的角为 ,且小正方形与大正方形面积之比为 ,则 的值为( )
A、 B、 C、 D、5. 已知实数 , 满足 , 则的最小值为( )A、 B、 C、 D、6. 在数学史上,为了三角计算的简便并追求计算的精确性,曾经出现过下列两种三角函数:定义 为角 的正矢,记作 ;定义 为角 的余矢,记作 .则下列说法正确的是( )A、 B、若 ,则 C、函数 在 上单调递增 D、函数 的最小值为7. 《周髀算经》中给出的弦图是由四个全等的直角三角形和中间一个小正方形拼成的一个大的正方形,若图中所示的角为 ,且小正方形与大正方形面积之比为 ,则 的值为( ) A、 B、 C、 D、8. 水车是一种利用水流动力进行灌溉的工具,是人类一项古老的发明,也是人类利用自然和改造自然的象征.如图是一个水车的示意图,已知水车逆时针匀速旋转一圈的时间是80秒,半径为3米,水车中心(即圆心)距水面1.5米.若以水面为 轴,圆心到水面的垂线为 轴建立直角坐标系,水车的一个水斗从出水面点 处开始计时,经过 秒后转到 点的位置,则点 到水面的距离 与时间 的函数关系式为( )
A、 B、 C、 D、8. 水车是一种利用水流动力进行灌溉的工具,是人类一项古老的发明,也是人类利用自然和改造自然的象征.如图是一个水车的示意图,已知水车逆时针匀速旋转一圈的时间是80秒,半径为3米,水车中心(即圆心)距水面1.5米.若以水面为 轴,圆心到水面的垂线为 轴建立直角坐标系,水车的一个水斗从出水面点 处开始计时,经过 秒后转到 点的位置,则点 到水面的距离 与时间 的函数关系式为( ) A、 B、 C、 D、9. 已知函数 ,函数 ,为奇函数,若函数 与 图象共有6个交点为 ,则 ( )A、0 B、6 C、12 D、2410. 对于集合 ,定义: 为集合 相对于 的“余弦方差”,则集合 相对于 的“余弦方差”为( )A、 B、 C、 D、11. 已知 sin= , 0<x< , 则 的值为( )
A、 B、 C、 D、9. 已知函数 ,函数 ,为奇函数,若函数 与 图象共有6个交点为 ,则 ( )A、0 B、6 C、12 D、2410. 对于集合 ,定义: 为集合 相对于 的“余弦方差”,则集合 相对于 的“余弦方差”为( )A、 B、 C、 D、11. 已知 sin= , 0<x< , 则 的值为( )
A、 B、 C、 D、12. 已知tan100°=K,则cos10°=( )A、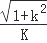 B、
B、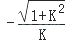 C、
C、 D、
D、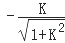 13. 已知则( )A、 B、 C、 D、14. 已知函数 , 给出下列四个结论:
13. 已知则( )A、 B、 C、 D、14. 已知函数 , 给出下列四个结论:①存在无数个零点; ②在上有最大值;
③若 , 则; ④区间是的单调递减区间.
其中所有正确结论的序号为( )
A、①②③ B、②③④ C、①③ D、①②③④15. 设.若对任意 , 都存在 , 使得 , 则可以是( )A、 B、 C、 D、16. 已知函数.若 , 且在区间上单调,则( )A、 B、或4 C、4 D、或17. 定义在实数集上的函数 , 如果 , 使得 , 则称为函数的不动点.给定函数 , , 已知函数 , , 在上均存在唯一不动点,分别记为 , 则( )A、 B、 C、 D、18. 给出定义:若函数在上可导,即存在,且导函数在上也可导,则称在上存在二阶导函数.记 , 若在上恒成立,则称在上为凸函数.以下四个函数在上是凸函数的有( )① , ② , ③ , ④.
A、4个 B、3个 C、2个 D、1个19. 若函数 在区间内没有最值,则的取值范围是( )A、 B、 C、 D、20. 若角 , , 且 , , 则( )A、 B、 C、 D、21. 洛阳栾川老君山形成于十九亿年前的大陆造山运动,造就了其千姿百态、群蜂竞秀、拔地通天、气势磅礴的景观,塑造了“华夏绿色心脏,世界地质奇观”的主题形象.某旅游爱好者在老君山山脚(处的海拔高度约为830m)测得山顶的仰角为45°,沿倾斜角为15°的斜坡向上走1200m到达处,在处测得山顶的仰角为75°,则老君山的海拔高度约为( )(参考数值: , ) A、1469m B、1869m C、2299m D、2399m22. 的值是( )A、16 B、8 C、4 D、223. 已知 , , 则( )A、 B、 C、 D、24. 1471年米勒向诺德尔教授提出的有趣问题:在地球表面的什么部位,一根垂直的悬杆看上去最长(即可见角最大).后人将其称为“米勒问题”,是载入数学史上的第一个极值问题.我们把地球表面抽象为平面 , 悬杆抽象为线段AB(或直线l上两点A,B),则上述问题可以转化为如下的数学模型:如图1,一条直线l垂直于一个平面 , 直线l有两点A,B位于平面的同侧,求平面上一点C,使得最大.建立如图2所示的平面直角坐标系.设A,B两点的坐标分别为 , .设点C的坐标为 , 当最大时,( )
A、1469m B、1869m C、2299m D、2399m22. 的值是( )A、16 B、8 C、4 D、223. 已知 , , 则( )A、 B、 C、 D、24. 1471年米勒向诺德尔教授提出的有趣问题:在地球表面的什么部位,一根垂直的悬杆看上去最长(即可见角最大).后人将其称为“米勒问题”,是载入数学史上的第一个极值问题.我们把地球表面抽象为平面 , 悬杆抽象为线段AB(或直线l上两点A,B),则上述问题可以转化为如下的数学模型:如图1,一条直线l垂直于一个平面 , 直线l有两点A,B位于平面的同侧,求平面上一点C,使得最大.建立如图2所示的平面直角坐标系.设A,B两点的坐标分别为 , .设点C的坐标为 , 当最大时,( ) A、2ab B、ab C、 D、25. 如图,函数的图象交坐标轴于点B,C,D,直线BC与曲线的另一交点为A.若 , 的重心为 , 则( )
A、2ab B、ab C、 D、25. 如图,函数的图象交坐标轴于点B,C,D,直线BC与曲线的另一交点为A.若 , 的重心为 , 则( ) A、函数在上单调递减 B、直线是函数图象的一条对称轴 C、 D、将的图象向左平移个单位长度,得到的图象26. 已知函数的图象向左平移个单位长度后,得到函数的图象,且的图象关于y轴对称,则的最小值为( )A、 B、 C、 D、27. 将函数的图象向左平移个单位长度后,得到函数的图象,若满足 , 则的最小值为( )A、 B、 C、 D、28. 如图所示的曲线就像横放的葫芦的轴截面的边缘线,我们把这样的曲线叫葫芦曲线(也像湖面上高低起伏的小岛在水中的倒影与自身形成的图形,也可以形象地称它为倒影曲线),它每过相同的间隔振幅就变化一次,且过点 , 其对应的方程为( , 其中为不超过x的最大整数,).若该葫芦曲线上一点N的横坐标为 , 则点N的纵坐标为( )
A、函数在上单调递减 B、直线是函数图象的一条对称轴 C、 D、将的图象向左平移个单位长度,得到的图象26. 已知函数的图象向左平移个单位长度后,得到函数的图象,且的图象关于y轴对称,则的最小值为( )A、 B、 C、 D、27. 将函数的图象向左平移个单位长度后,得到函数的图象,若满足 , 则的最小值为( )A、 B、 C、 D、28. 如图所示的曲线就像横放的葫芦的轴截面的边缘线,我们把这样的曲线叫葫芦曲线(也像湖面上高低起伏的小岛在水中的倒影与自身形成的图形,也可以形象地称它为倒影曲线),它每过相同的间隔振幅就变化一次,且过点 , 其对应的方程为( , 其中为不超过x的最大整数,).若该葫芦曲线上一点N的横坐标为 , 则点N的纵坐标为( ) A、 B、 C、 D、29. 已知函数的部分图象如图所示,其中B,C两点的纵坐标相等,若函数在上恰有3个零点,则实数a的取值范围是( )
A、 B、 C、 D、29. 已知函数的部分图象如图所示,其中B,C两点的纵坐标相等,若函数在上恰有3个零点,则实数a的取值范围是( ) A、 B、 C、 D、30. 函数的图象向右平移个单位得到函数 , 且在内没有零点,则的取值范围是( )A、 B、 C、 D、31. 已知函数 , 若存在实数、 , 使得 , 且 , 则的最大值为( )A、9 B、8 C、7 D、532. 筒车是我们古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图所示,已知筒车的半径为 ,筒车转轮的中心 到水面的距离为 ,筒车沿逆时针方向以角速度 转动,规定:盛水筒 对应的点 从水中浮现(即 时的位置)时开始计算时间,且以水轮的圆心 为坐标原点,过点 的水平直线为 轴建立平面直角坐标系 ,设盛水筒 从点 运动到点 时经过的时间为 (单位: ),且此时点 距离水面的高度为 (单位:米),筒车经过 第一次到达最高点,则下列叙述正确的是( )
A、 B、 C、 D、30. 函数的图象向右平移个单位得到函数 , 且在内没有零点,则的取值范围是( )A、 B、 C、 D、31. 已知函数 , 若存在实数、 , 使得 , 且 , 则的最大值为( )A、9 B、8 C、7 D、532. 筒车是我们古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图所示,已知筒车的半径为 ,筒车转轮的中心 到水面的距离为 ,筒车沿逆时针方向以角速度 转动,规定:盛水筒 对应的点 从水中浮现(即 时的位置)时开始计算时间,且以水轮的圆心 为坐标原点,过点 的水平直线为 轴建立平面直角坐标系 ,设盛水筒 从点 运动到点 时经过的时间为 (单位: ),且此时点 距离水面的高度为 (单位:米),筒车经过 第一次到达最高点,则下列叙述正确的是( )
 A、当 时,点 与点 重合 B、当 时, 一直在增大 C、当 时,盛水筒有 次经过水平面 D、当 时,点 在最低点
A、当 时,点 与点 重合 B、当 时, 一直在增大 C、当 时,盛水筒有 次经过水平面 D、当 时,点 在最低点