人教A版数学高一（上）期末提分专题复习10 三角函数的应用

试卷更新日期：2023-12-22 类型：复习试卷

进入出卷网下载

一、选择题

1. 为了研究钟表秒针针尖的运动变化规律，建立如图所示的平面直角坐标系，设秒针针尖位置为点 $P (x ， y)$ ．若初始位置为点 $P_{0} (\frac{\sqrt{2}}{2} ， \frac{\sqrt{2}}{2})$ ，秒针从 $P_{0}$ （规定此时 $t = 0$ ）开始沿顺时针方向转动，若点P的纵坐标为y， $t \in [0 ， 60]$ ，则 $y < - \frac{\sqrt{3}}{2}$ 时t的取值范围为（）

A、 $(\frac{25}{2} ， \frac{45}{2})$ B、 $(\frac{35}{2} ， \frac{55}{2})$ C、 $(\frac{45}{2} ， \frac{65}{2})$ D、 $(\frac{55}{2} ， \frac{75}{2})$

查看试题解析
2. 在西双版纳热带植物园中有一种原产于南美热带雨林的时钟花，其花开花谢非常有规律.有研究表明，时钟花开花规律与温度密切相关，时钟花开花所需要的温度约为 $2 0^{∘} C$ ，但当气温上升到 $3 1^{∘} C$ 时，时钟花基本都会凋谢.在花期内，时钟花每天开闭一次.已知某景区有时钟花观花区，且该景区6时 $\sim 14$ 时的气温 $T$ （单位： $^{∘} C$ ）与时间 $t$ （单位：小时）近似满足函数关系式 $T = 25 + 10 s i n (\frac{π}{8} t + \frac{3 π}{4})$ ，则在6时 $\sim 14$ 时中，观花的最佳时段约为（）（参考数据： $s i n \frac{π}{5} \approx 0.6$ ）

A、6.7时 $\sim 11.6$ 时 B、6.7时 $\sim 12.2$ 时 C、8.7时 $\sim 11.6$ 时 D、8.7时 $\sim 12.2$ 时

查看试题解析
3. “寸影千里”法是《周髀算经》中记载的一种远距离测量的估算方法，其具体方法是在同一天（如夏至）的正午，于两地分别竖起同高的标杆，然后测量标杆的影长，并根据“日影差一寸，实地相距千里”的原则推算两地距离．如图，某人在夏至的正午分别在同一水平面上的A，B两地竖起高度均为a寸的标杆 $A E$ 与 $B F$ ， $A C$ 与 $B D$ 分别为标杆 $A E$ 与 $B F$ 在地面的影长，再按影长 $A C$ 与 $B D$ 的差结合“寸影千里”来推算A，B两地的距离．记 $∠ C E A = α ， ∠ B D F = β (β < \frac{π}{2} - α)$ ，则按照“寸影千里”的原则，A，B两地的距离大约为（）

A、 $\frac{1000 a s i n (α + β)}{s i n α s i n β}$ 里 B、 $\frac{1000 a s i n (α + β)}{s i n α c o s β}$ 里 C、 $\frac{1000 a c o s (α + β)}{s i n β c o s α}$ 里 D、 $\frac{1000 a c o s (α + β)}{c o s α c o s β}$ 里

查看试题解析
4. 江西南昌的滕王阁，位于南昌沿江路赣江东岸，始建于唐永徽四年（即公元653年），是古代江南唯一的皇家建筑.因初唐诗人王勃所作《滕王阁序》而名传千古，流芳后世，被誉为“江南三大名楼”之首（另外两大名楼分别为岳阳的岳阳楼与武汉的黄鹤楼）.小张同学为测量滕王阁的高度，选取了与底部水平的直线 $D F$ ，将自制测量仪器分别放置于 $D$ ， $E$ 两处进行测量.如图，测量仪器高 $A D = 2$ m，点 $P$ 与滕王阁顶部平齐，并测得 $∠ C B P = 2 ∠ C A P = 60 °$ ， $A B = 64$ m，则小张同学测得滕王阁的高度约为（参考数据 $\sqrt{3} \approx 1.732$ ）（）

A、50m B、55.5m C、57.4m D、60m

查看试题解析
5. 如图，弹簧挂着一个小球作上下运动，小球在t秒时相对于平衡位置的高度h（厘米）由如下关系式确定： $h = 2 s i n (\frac{π}{6} t + ϕ)$ ， $t \in [0 ， + \infty)$ ， $ϕ \in (- π ， π)$ .已知当 $t = 2$ 时，小球处于平衡位置，并开始向下移动，则小球在 $t = 0$ 秒时h的值为（）

A、-2 B、2 C、 $- \sqrt{3}$ D、 $\sqrt{3}$

查看试题解析
6. 岳阳楼与湖北武汉黄鹤楼、江西南昌滕王阁并称为“江南三大名楼”，是“中国十大历史文化名楼”之一，世称“天下第一楼”．因范仲淹作《岳阳楼记》使得岳阳楼著称于世．小李为测量岳阳楼的高度选取了与底部水平的直线AC，如图，测得 $∠ D A C = 30 °$ ， $∠ D B C = 60 °$ ， $A B = 14$ 米，则岳阳楼的高度CD为（）

A、 $6 \sqrt{3}$ 米 B、 $7 \sqrt{3}$ 米 C、 $8 \sqrt{3}$ 米 D、 $9 \sqrt{3}$ 米

查看试题解析
7. 已知函数 $f (x) = A s i n (ω x + φ)$ （ $A > 0$ ， $ω > 0$ ， $| φ | < \frac{π}{2}$ ），M是函数 $f (x)$ 图象的一个最高点，K，N是函数图象上与它距离最近的两个对称中心， $Δ K M N$ 是边长为1的正三角形， $f (1) = \frac{3}{4}$ ，若函数 $f (x + t)$ 为偶函数，则 $| t |$ 的最小值为（）

A、 $\frac{1}{12}$ B、 $\frac{1}{6}$ C、 $\frac{5}{6}$ D、1

查看试题解析
8. 已知函数 $f (x) = s i n ω x$ ， $g (x) = c o s ω x$ ， $ω > 0$ 的图象的3个交点可以构成一个等腰直角三角形，则 $ω$ 的最小值为（）

A、 $\frac{π}{2}$ B、 $π$ C、 $\frac{\sqrt{2}}{2} π$ D、 $\sqrt{2} π$

查看试题解析
9. 如图，摩天轮上一点 $P$ 在 $t$ 时刻距离地面的高度满足 $y = A s i n (ω t + φ) + B$ ， $A > 0$ ， $ω > 0$ ， $φ \in [- π ， π]$ ，已知某摩天轮的半径为50米，点 $O$ 距地面的高度为60米，摩天轮做匀速运动，每10分钟转一圈，点 $P$ 的起始位置在摩天轮的最低点，则 $y$ （米）关于 $t$ （分钟）的解析式为（）

A、 $y = 60 - 50 s i n \frac{π}{5} t$ （ $t > 0$ ） B、 $y = 60 - 50 c o s \frac{π}{5} t$ （ $t > 0$ ） C、 $y = 60 - 50 c o s \frac{π}{10} t$ （ $t > 0$ ） D、 $y = 60 - 50 s i n \frac{π}{10} t$ （ $t > 0$ ）

查看试题解析
10. 图1是南北方向、水平放置的圭表（一种度量日影长的天文仪器，由“圭”和“表”两个部件组成）示意图，其中表高为h，日影长为l.图2是地球轴截面的示意图，虚线表示点A处的水平面.已知某测绘兴趣小组在冬至日正午时刻（太阳直射点的纬度为南纬 $23 ° 2 6^{'}$ ）在某地利用一表高为 $2 d m$ 的圭表按图1方式放置后，测得日影长为 $2.98 d m$ ，则该地的纬度约为北纬（）（参考数据： $t a n 34 ° \approx 0.67$ ， $t a n 56 ° \approx 1.49$ ）

A、 $23 ° 2 6^{'}$ B、 $32 ° 3 4^{'}$ C、 $34 °$ D、 $56 °$

查看试题解析

二、多项选择题

11. 如图，一圆形摩天轮的直径为100米，圆心O到水平地面的距离为60米，最上端的点记为Q，现在摩天轮开始逆时针方向匀速转动，30分钟转一圈，以摩天轮的中心为原点建立平面直角坐标系，则下列说法正确的是（）

A、点Q距离水平地面的高度与时间的函数为 $h (t) = 50 s i n (\frac{π t}{15} + \frac{π}{3}) + 10$ B、点Q距离水平地面的高度与时间的函数的对称中心坐标为 $(15 k ， 60) (k \in Z)$ C、经过10分钟点Q距离地面35米 D、摩天轮从开始转动一圈，点Q距离水平地面的高度不超过85米的时间为20分钟

查看试题解析
12. 某商场前有一块边长为60米的正方形地皮，为了方便消费者停车，拟划出一块矩形区域用于停放电动车等，同时为了美观，建造扇形花坛，现设计两种方案如图所示，方案一： $D E = \frac{2}{3} D F = \frac{1}{3} D A$ ， $R$ 在线段 $E F$ 上且 $R T / / C D$ ，方案二： $R$ 在圆弧上且 $R T / / C D$ ．若花坛区域工程造价0.2万元/平方米，停车区域工程造价为0.1万元/平方米，则下列说法正确的是（）

A、两个方案中矩形停车区域的最大面积为2400平方米 B、两个方案中矩形停车区域的最小面积为1200平方米 C、方案二中整个工程造价最低为 $(120 + 40 π)$ 万元 D、两个方案中整个工程造价最高为 $(240 + 20 π)$ 万元

查看试题解析
13. 衢州市柯城区沟溪乡余东村是中国十大美丽乡村，也是重要的研学基地，村口的大水车，是一道独特的风景.假设水轮半径为4米（如图所示），水轮中心O距离水面2米，水轮每60秒按逆时针转动一圈，如果水轮上点P从水中浮现时（图中 $P_{0}$ ）开始计时，则（）

A、点P第一次达到最高点，需要20秒 B、当水轮转动155秒时，点P距离水面2米 C、在水轮转动的一圈内，有15秒的时间，点P距水面超过2米 D、点P距离水面的高度h（米）与t（秒）的函数解析式为 $h = 4 s i n (\frac{π}{30} t - \frac{π}{6}) + 2$

查看试题解析
14. 血压是指血液在血管内流动时作用单位面积血管壁的侧压力，它是推动血液在血管内流动的动力.血压的最大值、最小值分别称为收缩压和舒张压.在未使用抗高血压药的前提下，18岁以上成人收缩压 $\geq 140 m m H g$ 或舒张压 $\geq 90 m m H g$ ，则说明这位成人有高血压.设从未使用过抗高血压药的小王今年26岁，从某天早晨6点开始计算（即早晨6点起， $t = 0$ ），他的血压 $p (t)$ （单位：）与经过的时间 $t$ （单位： $h$ ）满足关系式 $p (t) = 116 + 22 s i n (\frac{π}{6} t + \frac{π}{3})$ ，则（）

A、血压 $p (t)$ 的最小正周期为6 B、当天下午 $3$ 点小王的血压为105 C、当天小王有高血压 D、当天小王的收缩压与舒张压之差为44

查看试题解析
15. 为了研究钟表秒针针尖的运动变化规律，建立如图所示的平面直角坐标系，设秒针针尖位置为点 $P (x ， y)$ ．若初始位置为点 $P_{0} (\frac{1}{2} ， \frac{\sqrt{3}}{2})$ ，秒针从 $P_{0}$ （规定此时 $t = 0$ ）开始沿顺时针方向转动，则点P的纵坐标y与时间t的函数关系式可能为（）

A、 $y = 2 \sin (- \frac{π}{30} t + \frac{π}{3})$ B、 $y = - \sin (\frac{π}{60} t - \frac{π}{3})$ C、 $y = \sin (- \frac{π}{30} t + \frac{π}{3})$ D、 $y = \cos (\frac{π}{30} t + \frac{π}{6})$

查看试题解析

三、填空题

16. 某城市一年中12个月的平均气温与月份的关系可近似地用三角函数 $y = a + A c o s [\frac{π}{6} (x - 6)]$ （x=1，2，3，…，12）来表示，已知6月份的月平均气温为28℃；12月份的月平均气温为18℃，则10月份的平均气温为℃.

查看试题解析
17. 摩天轮是一种大型转轮状的机械建筑设施，某摩天轮最高点距离地面高度128米，转盘直径为120米，设置有48个座舱，开启后按逆时针方向匀速旋转，游客在座舱转到距离地面最近的位置进舱，转一周需要30分钟.若游客甲坐上摩天轮的座舱，开始旋转 $t$ 分钟后距离地面的高度为 $h$ 米，则 $h$ 关于 $t$ 的函数解析式为；若游客甲在 $t_{1}$ ， $t_{2}$ 时刻距离地面的高度相等，则 $t_{1} + t_{2}$ 的最小值为.

查看试题解析
18. 台球赛的一种得分战术手段叫做“斯诺克”：在白色本球与目标球之间，设置障碍，使得本球不能直接击打目标球.如图，某场比赛中，某选手被对手做成了一个“斯诺克”，本球需经过边 $B C$ ， $C D$ 两次反弹后击打目标球N，点M到 $C D ， B C$ 的距离分别为 $200 c m ， 60 c m$ ，点N到 $C D ， B C$ 的距离分别为 $80 c m ， 120 c m$ ，将M，N看成质点，本球在M点处，若击打成功，则 $t a n θ =$ ．

查看试题解析
19. 在平面直角坐标系xOy中，先将线段OP绕原点O按逆时针方向旋转角 $θ$ ，再将旋转后的线段OP的长度变为原来的 $ρ (ρ > 0)$ 倍得到 $O P_{1}$ ，我们把这个过程称为对点P进行一次 $T (θ ， ρ)$ 变换得到点 $P_{1}$ ，例如对点 $(1 ， 0)$ 进行一次 $T (\frac{π}{2} ， 3)$ 变换得到点 $(0 ， 3)$ ．若对点 $A (1 ， 0)$ 进行一次 $T (\frac{2 π}{3} ， 2)$ 变换得到点 $A_{1}$ ，则 $A_{1}$ 的坐标为；若对点 $B (\frac{4}{5} ， \frac{3}{5})$ 进行一次 $T (θ ， ρ)$ 变换得到点 $B_{1} (- 3 ， - 4)$ ，对点 $B_{1}$ 再进行一次 $T (θ ， ρ)$ 变换得到点 $B_{2}$ ，则 $B_{2}$ 的坐标为．

查看试题解析
20. 摩天轮是一种大型转轮状的机械建筑设施，稳坐于永乐桥之上的“天津之眼”作为世界上唯一一座建在桥上的摩天轮，其巧夺天工和奇思妙想确是当之无愧的“世界第一”.如图，永乐桥摩天轮的直径为 $110 m$ ，到达最高点时，距离地面的高度为 $120 m$ ，能看到方圆 $40 km$ 以内的景致，是名副其实的“天津之眼”.实际上，单从高度角度来看，天津之眼超越了曾大名鼎鼎的伦敦之眼而跃居世界第一.永乐桥摩天轮设置有48个座舱，开启后按逆时针方向匀速旋转，游客在座舱转到距离地面最近的位置进舱，转一周大约需要 $30 \min$ .游客甲坐上摩天轮的座舱，开始转到 $t \min$ 后距离地面的高度为 $H m$ ，则转到 $10 \min$ 后距离地面的高度为 $m$ ，在转动一周的过程中， $H$ 关于 $t$ 的函数解析式为.

查看试题解析
21. 某城市一年中12个月的平均气温与月份的关系可近似地用三角函数 $y = A \cos [\frac{π}{6} (x - 6)] + B (x = 1, 2, ..., 12)$ 来表示.已知 $6$ 月份的平均气温最高，为 $28$ ℃，12月份的月平均气温最低，为18℃，则10月份的平均气温为℃.

查看试题解析
22. 已知直线 $y = a (x + 2) (a > 0)$ 与函数 $y = | \cos x |$ 的图像恰有四个公共点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ ， $C (x_{3} ， y_{3})$ ， $D (x_{4} ， y_{4})$ ，其中 $x_{1} < x_{2} < x_{3} < x_{4}$ ，则 $x_{4} + \frac{1}{\tan x_{4}} =$ ．

查看试题解析
23. 某城市一年中12个月的平均气温与月份的关系可近似地用三角函数 $y = a + A cos [\frac{π}{6} (x - 6)] (x = 1 ， 2 ， 3 ， \dots ， 12)$ 来表示，已知6月份的月平均气温最高，为 $28 ° C$ ，12月份的月平均气温最低，为 $18 ° C$ ，则10月份的平均气温值为 $° C$ ．

查看试题解析
24. 若电灯B可在过桌面上一点O且垂直于桌面的垂线上移动，桌面上有与点O距离为a的另一点A，问电灯与点0的距离，可使点A处有最大的照度？（∠BAO=φ，BA=r，照度与sinφ成正比，与r²成反比）

查看试题解析
25. 在同一平面直角坐标系中，函数y=cos( $\frac{x}{2}$ + $\frac{3 π}{2}$ ) $(x \in [0 ， 2 π])$ 的图象和直线y= $\frac{1}{2}$ 的交点个数是个

查看试题解析

四、解答题

26. 已知函数 $y = f (x)$ ， $x \in D$ ，如果对于定义域D内的任意实数x，对于给定的非零常数P，总存在非零常数T，恒有 $f (x + T) < P \cdot f (x)$ 成立，则称函数 $f (x)$ 是D上的P级递减周期函数，周期为T；若恒有 $f (x + T) = P \cdot f (x)$ 成立，则称函数 $f (x)$ 是D上的P级周期函数，周期为T.

(1)、判断函数 $f (x) = x^{2} + 3$ 是R上的周期为1的2级递减周期函数吗，并说明理由？

(2)、已知 $T = \frac{π}{2}$ ， $y = f (x)$ 是 $[0 ， + ∞)$ 上的P级周期函数，且 $y = f (x)$ 是 $[0 ， + ∞)$ 上的严格增函数，当 $x \in [0 ， \frac{π}{2})$ 时， $f (x) = s i n x + 1$ .求当 $x \in [\frac{π}{2} n ， \frac{π}{2} (n + 1)) (n \in N^{*})$ 时，函数 $y = f (x)$ 的解析式，并求实数P的取值范围；

(3)、是否存在非零实数k，使函数 $f (x) = {(\frac{1}{2})}^{x} \cdot c o s k x$ 是R上的周期为T的T级周期函数？请证明你的结论.

查看试题解析
27. 某小区围墙一角要建造一个水池和两条小路．如图，四边形 $A B C D$ 中， $D A ⊥ A B$ ， $D C ∥ A B$ ，以 $A$ 为圆心、 $A D$ 为半径的四分之一圆及 $A B$ 与 $A D$ 圈成的区域为水池，线段 $D C$ 和 $C B$ 为两条小路，且 $C B$ 所在直线与圆弧相切．已知 $A D = 10$ 米，设 $∠ D A C = θ$ （ $0 < θ < \frac{π}{4}$ ），那么当 $θ$ 为多少时，才能使两条小路长之和 $D C + C B$ 最小？最小长度是多少？

查看试题解析
28. 如图，一个直径为 $5 m$ 的水车按逆时针方向每分钟转1.8圈，水车的中心 $O$ 距离水面的高度为 $1.25 m$ ，水车上的盛水筒 $P$ 到水面的距离为 $h$ （单位： $m$ ）（在水面下则 $h$ 为负数），若以盛水筒 $P$ 刚浮出水面时开始计时，则 $h$ 与时间 $t$ （单位： $s$ ）之间的关系为 $h = A s i n (ω t + φ) + b (A > 0 ， ω > 0 ， | φ | < \frac{π}{2})$ .

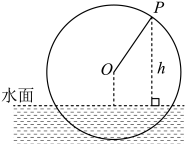(1)、求 $h$ 与 $t$ 的函数解析式；

(2)、求在一个旋转周期内，盛水筒 $P$ 在水面以上的时长.

查看试题解析
29. 某游乐场的摩天轮示意图如图．已知该摩天轮的半径为30米，轮上最低点与地面的距离为2米，沿逆时针方向匀速旋转，旋转一周所需时间为 $T = 24$ 分钟．在圆周上均匀分布12个座舱，标号分别为 $1 ~ 12$ （可视为点），现从图示位置，即1号座舱位于圆周最右端时开始计时，旋转时间为 $t$ 分钟．

(1)、当 $t = 6$ 时，求1号座舱与地面的距离；

(2)、记1号座舱与5号座舱高度之差的绝对值为 $H$ 米，若在 $0 ≤ t ≤ t_{0}$ 这段时间内， $H$ 恰有三次取得最大值，求 $t_{0}$ 的取值范围．

查看试题解析
30. 一个半径为2米的水轮如图所示，水轮圆心O距离水面1米．已知水轮按逆时针作匀速转动，每6秒转一圈，如果当水轮上点P从水中浮现时（图中点 $P_{0}$ ）开始计算时间．

(1)、以过点O且平行于水轮所在平面与水面的交线L的直线为x轴，以过点O且与水面垂直的直线为y轴，建立如图所示的直角坐标系，试将点P距离水面的高度h（单位：米）表示为时间t（单位：秒）的函数；

(2)、在水轮转动的任意一圈内，有多长时间点P距离水面的高度不低于2米？

查看试题解析