人教A版数学高一（上）期末提分专题复习4 指数函数

试卷更新日期：2023-12-22 类型：复习试卷

进入出卷网下载

一、选择题

1. 化简二次根式 $\sqrt{- 8 a^{3}}$ 的结果为（）

A、 $- 2 a \sqrt{- 2 a}$ B、 $2 a \sqrt{2 a}$ C、 $2 a \sqrt{- 2 a}$ D、 $- 2 a \sqrt{2 a}$

查看试题解析
2. 下列根式与分数指数幂的互化正确的是（）

A、 $- \sqrt{x} = {(- x)}^{\frac{1}{2}}$ B、 $\sqrt[6]{y^{2}} = y^{\frac{1}{3}} (y < 0)$ C、 $x^{- \frac{1}{3}} = \frac{1}{\sqrt[3]{x}} (x > 0)$ D、 ${[\sqrt[3]{(- x)^{2}}]}^{\frac{3}{4}} = x^{\frac{1}{2}}$

查看试题解析
3. 基本再生数 $R_{0}$ 与世代间隔 $T$ 是新冠肺炎的流行病学基本参数．基本再生数指一个感染者传染的平均人数，世代间隔指相邻两代间传染所需的平均时间．在新冠肺炎疫情初始阶段，可以用指数模型： $I (t) = e^{r t}$ 描述累计感染病例数 $I (t)$ 随时间 $t$ (单位：天)的变化规律，指数增长率 $r$ 与 $R_{0}$ ， $T$ 近似满足 $R_{0} = 1 + r T$ ．有学者基于已有数据估计出 $R_{0}$ =3.07， $T$ =6．据此，在新冠肺炎疫情初始阶段，累计感染病例数增加1倍需要的时间约为(参考数据：ln2≈0.69)（）

A、1.5天 B、2天 C、2.5天 D、3.5天

查看试题解析
4. 函数 $y = a^{x + 2} + 1$ （ $a > 0$ 且 $a \neq 1$ ）的图象过定点（）

A、 $(- 1 ， 1)$ B、 $(2 ， 1)$ C、 $(- 2 ， 2)$ D、 $(2 ， - 2)$

查看试题解析
5. 函数 $y = a^{x} - \frac{1}{a} (a > 0 ， a \neq 1)$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
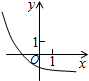6. 已知函数 $y = a {(\frac{1}{2})}^{x} + b$ 的图象过原点，且无线接近直线 $y = 2$ 但不与该直线相交，则（）

A、 $a = - 2$ ， $b = 2$ B、 $a = 2$ ， $b = 2$ C、 $a = - 1$ ， $b = 2$ D、 $a = 2$ ， $b = 1$

查看试题解析
7. 已知 $a = 3^{1.2} ， b = 1 . 2^{0} ， c = {(\frac{1}{3})}^{- 0.9}$ ，则 $a ， b ， c$ 的大小关系是（）

A、 $a < c < b$ B、 $c < b < a$ C、 $c < a < b$ D、 $b < c < a$

查看试题解析

8. 提丢斯一波得定则，简称“波得定律”，是表示各行星与太阳平均距离的一种经验规则.它是在1766年德国的一位中学教师戴维·提丢斯发现的.后来被柏林天文台的台长波得归纳成了一个如下经验公式来表示：记太阳到地球的平均距离为1，若某行星的编号为n，则该行星到太阳的平均距离表示为

a + b \times 2^{n - 1}

，那么编号为9的行星用该公式推得的平均距离位于（）

行星	金星	地球	火星	谷神星	木星	土星	天王星	海王星
编号	1	2	3	4	5	6	7	8
公式推得值	0.7	1	1.6	2.8	5.2	10	19.6	38.8
实测值	0.72	1	1.52	2.9	5.2	9.54	19.18	30.06

A、

(30 ， 50)

B、

(50 ， 60)

C、

(60 ， 70)

D、

(70 ， 80)

查看试题解析

9. 欧拉是瑞士著名数学家，他首先发现： $e^{i θ} = \cos θ + i \sin θ$ （e为自然对数的底数，i为虚数单位），此结论被称为“欧拉公式”，它将指数函数的定义域扩大到复数集，建立了三角函数和指数函数的关系．根据欧拉公式可知， $e^{i π}$ ＝（）

A、1 B、0 C、－1 D、1＋i

查看试题解析

二、多项选择题

10. 下列表达式中不正确的是（）

A、 $a^{\frac{5}{3}} \div a^{\frac{2}{3}} = a (a > 0)$ B、 ${(a^{2})}^{3} = a^{6}$ C、 $\frac{\sqrt{- a^{3}}}{a} = \sqrt{- a} (a \neq 0)$ D、 $\sqrt[4]{a^{2}} = a^{0.5}$

查看试题解析
11. 下列各式的值相等的是（）

A、 $(- 1)^{\frac{1}{3}}$ 和 $\sqrt[6]{(- 1)^{2}}$ B、 $3^{\frac{4}{3}}$ 和 $\frac{1}{3^{- \frac{4}{3}}}$ C、 $\sqrt{2}$ 和 $4^{\frac{1}{4}}$ D、 $4^{- \frac{3}{2}}$ 和 ${(\frac{1}{2})}^{- 3}$

查看试题解析
12. 已知 $3^{a} = 2 ， 5^{b} = 3$ ，则下列结论正确的是（）

A、 $a > b$ B、 $a + \frac{1}{a} > b + \frac{1}{b}$ C、 $a + b < 2 a b$ D、 $a + a^{b} < b + b^{a}$

查看试题解析
13. 下列结论中，正确的是（）

A、函数 $y = 2^{x - 1}$ 是指数函数 B、函数 $y = {(\frac{1}{3})}^{- x^{2} + 2 x}$ 的单调增区间是 $(1 ， + \infty)$ C、若 $a^{m} > a^{n} (a > 0 ， a \neq 1)$ 则 $m > n$ D、函数 $f (x) = a^{x - 2} - 3 (a > 0 ， a \neq 1)$ 的图像必过定点 $(2 ， - 2)$

查看试题解析

三、填空题

14. 计算： $1 6^{- \frac{1}{2}} - {(\frac{27}{8})}^{\frac{2}{3}} + \sqrt[4]{{(3 - π)}^{4}} =$ ．

查看试题解析
15. 若 $3^{m} - 3^{- m} = 2 \sqrt{3}$ ，则 $9^{m} + 9^{- m}$ 的值为.

查看试题解析
16. 若函数 $y = a^{x - 2} + 3$ （ $a > 0$ 且 $a \neq 1)$ 的图象恒过定点 $Q$ ，且点 $Q$ 在幂函数 $f (x) = x^{m}$ 的图象上，则 $f (4) =$ .

查看试题解析
17. 已知函数 $f (x) = {\begin{array}{l} | x + 2 | ， - 4 \leq x < 0 \\ 2 - e^{x} ， x \geq 0 \end{array}$ ，若存在 $x_{1} ， x_{2} ， x_{3} (x_{1} < x_{2} < x_{3})$ ，使 $f (x_{1}) = f (x_{2}) = f (x_{3})$ ，则 $x_{1} + x_{2} + x_{3}$ 的取值范围是．

查看试题解析
18. 已知函数 $f (x) = 3 a^{x + 2} - 1$ 过定点 $M$ 的坐标为．

查看试题解析
19. 若指数函数 $y = a^{x}$ 在区间 $[0 ， 1]$ 上的最大值和最小值的差为 $\frac{1}{2}$ ，则底数a的值为．

查看试题解析
20. 若函数 $f (x) = {\begin{cases} - x + 3 - 3 a ， x < 0 \\ a^{x} ， x \geq 0 \end{cases}$ 是 $R$ 上的减函数，则实数 $a$ 的取值范围是．

查看试题解析
21. 比较两个值的大小： $1 . 2^{0.5}$ $0 . 5^{1.2}$ （请用“>”，“=”“<”填空）

查看试题解析
22. 在做好疫情防护工作时，常常用到酒精消毒.某人从盛有1L纯酒精的容器中倒出 $\frac{1}{4}$ L，然后用水填满：再倒出 $\frac{1}{4}$ L，又用水填满，连续进行5次操作，容器中的纯酒精还剩下多少L.

查看试题解析

四、解答题

23. 若 $x > 0$ ， $y > 0$ ，且满足 $\sqrt{x} (\sqrt{x} + \sqrt{y}) = 3 \sqrt{y} (\sqrt{x} + 5 \sqrt{y})$ ，求 $\frac{2 x + 2 \sqrt{x y} + 3 y}{x - \sqrt{x y} + y}$ 的值.

查看试题解析
24. 计算：

(1)、求值： $0.12 5^{- \frac{1}{3}} - {(\frac{9}{8})}^{0} + {[{(- 2)}^{2}]}^{\frac{3}{2}} + {(\sqrt{2} \times \sqrt[3]{3})}^{6}$

(2)、已知： $a^{\frac{1}{2}} + a^{- \frac{1}{2}} = 3$ ，求 $\frac{a^{2} + a^{- 2} + 3}{a + a^{- 1} - 2}$ 的值

查看试题解析
25. 对下列式子化简求值

(1)、求值： $(\sqrt[3]{3})^{6} \times (\frac{27}{8})^{- \frac{2}{3}} + 202 3^{0} ；$

(2)、已知 $a^{x} + a^{- x} = 4 (a > 0$ 且 $a \neq 1)$ ，求 $a^{\frac{x}{2}} + a^{- \frac{x}{2}}$ 的值.

查看试题解析
26. 已知函数 $f (x) = 2^{x} - 4^{x} ， x \in [- 2 ， 1]$

(1)、求 $f (x)$ 的值域：

(2)、若对 $\forall x \in [- 2 ， 1]$ ，不等式 $f (x) > 2 - m 2^{x}$ 恒成立，求实数 $m$ 的取值范围？

查看试题解析
27. 已知函数 $f (x) = b \cdot a^{x}$ （ $a > 0$ ，且 $a \neq 1$ ）的图象经过点 $A (1 ， 4)$ ， $B (3 ， 16)$ .

(1)、求函数 $f (x)$ 的解析式；

(2)、设函数 $g (x) = f (x) - f (- x) (x \geq 2)$ ，求函数 $g (x)$ 的值域

查看试题解析
28. 已知函数 $f (x) = a^{2 x} - 2 a^{x} - 1$ ，其中 $a > 0$ 且 $a \neq 1$ .

(1)、若 $f (x)$ 的图象经过一个定点，写出此定点的坐标；

(2)、若 $a = 2$ ，求 $f (x)$ 的最小值；

(3)、若 $f (x)$ 在区间 $[0 ， 1]$ 上的最大值为2，求a的值.

查看试题解析
29. 已知函数 $f (x) = a^{x - 1}$ （ $a > 0$ ，且 $a \neq 1$ ）.

(1)、若函数 $f (x)$ 的图象过点 $(3 ， 4)$ ，求实数a的值；

(2)、若 $a = \frac{1}{2}$ ，当 $x \in [2 ， + \infty)$ 时，求函数 $f (x)$ 的取值范围；

(3)、求关于x的不等式 $f (x) > a^{3}$ 的解集.

查看试题解析
30. 已知集合 $M = {x | \frac{1}{8} < 2^{x} < 32}$ ， $N = {x | 0 < x < 8}$ ， $C = {x | a < x < 2 a - 1}$ ．

(1)、求 $M ∩ N$ ；

(2)、若 $M ∪ C = M$ ，求实数 $a$ 的取值范围．

查看试题解析
31. 已知函数 $f (x) = \frac{2^{x} - m}{2^{x} + 1}$ 为奇函数．

(1)、求实数m的值及函数 $f (x)$ 的值域；

(2)、若 $f (\frac{1}{x - 1}) - f (2) > 0$ ，求x的取值范围．

查看试题解析
32. 已知指数函数 $y = f (x)$ 的图象过点 $(- 2 ， 9)$ .

(1)、求函数 $f (x)$ 的解析式

(2)、试比较 $f (- 0.3) ， f (0.3) ， 1$ 这三个数的大小，并说明理由；

(3)、若 $f (- m^{2} + m + 1) < 1$ ，求实数 $m$ 的取值范围.

查看试题解析
33. 某医学研究所研发一种药物，据监测，如果成人在2h内按规定的剂量注射该药，在注射期间，血液中的药物含量呈线性增加；停止注射后，血液中的药物含量呈指数衰减．每毫升血液中的药物含量y（μg）与服药后的时间t（h）之间近似满足如图所示的曲线，其中OA是线段，曲线段AB是函数 $y = k a^{t}$ （ $t \geq 2$ ， $a > 0$ ， k，a是常数）的图象，且 $A (2 ， 8)$ ， $B (4 ， 2)$ ．

(1)、写出注射该药后每毫升血液中药物含量y关于时间t的函数关系式；

(2)、据测定：每毫升血液中药物含量不少于1μg时治疗有效，如果某人第一次注射药物为早上8点，为保持疗效，第二次注射药物最迟是当天几点钟？

(3)、若按（2）中的最迟时间注射第二次药物，则第二次注射后再过1.5h，该人每毫升血液中药物含量为多少μg（精确到0.1μg）？

查看试题解析
34. 已知函数 $f (x) = | \frac{2^{x} - 1}{2^{x} + 1} |$ .

(1)、判断函数 $f (x)$ 的奇偶性，并说明理由；

(2)、若存在正实数 $x_{1} ， x_{2}$ 且 $x_{2} > x_{1}$ ，使得 $f (x)$ 在区间 $[x_{1} ， x_{2}]$ 上的值域为 $[\frac{a}{2^{x_{1} + 1} - 3} ， \frac{a}{2^{x_{2} + 1} - 3}]$ ，求实数 $a$ 的取值范围.

查看试题解析
35. 已知函数 $f (x) = \frac{4^{x}}{4^{x} + 2}$ ；

(1)、若 $0 < a < 1$ ，求 $f (a) + f (1 - a)$ 的值；

(2)、求 $f (\frac{1}{2021}) + f (\frac{2}{2021}) + f (\frac{3}{2021}) + \cdot \cdot \cdot + f (\frac{2020}{2021})$ 的值．

查看试题解析