2023-2024学年浙教版数学九年级(上)期末仿真模拟卷(五)(九上全册)
试卷更新日期:2023-12-22 类型:期末考试
一、选择题(每题4分,共40分)
-
1. 如果线段b是线段a,c的比例中项,a:c = 4:9,那么下列结论中正确的是( )A、a:b = 4:9 B、b:c = 2:3 C、a:b = 3:2 D、b:c = 3:22. 九年级一班有25名男生和20名女生,从中随机抽取一名作为代表参加校演讲比赛.下列说法正确的是( )A、抽到男生和女生的可能性一样大 B、抽到男生的可能性大 C、抽到女生的可能性大 D、抽到男生或女生的可能性大小不能确定3. 二次函数y=(x-3)(x+2)的图象的对称轴是( )A、直线x=3 B、直线x=-2 C、直线x= D、直线x=4. 如图,AC为⊙O的直径,点B在⊙O上.下列说法正确的是( )
 A、图中的弦有AB,AC,BC,AO B、弦BC所对的弧是 , C、图中的优弧是 D、图中的劣弧是5. 大数据分析技术为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的健康码(绿码)示意图,用黑白打印机打印于边长为 的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量反复实验,发现点落入黑色部分的频率稳定在 左右,据此可以估计黑色部分的总面积约为( )
A、图中的弦有AB,AC,BC,AO B、弦BC所对的弧是 , C、图中的优弧是 D、图中的劣弧是5. 大数据分析技术为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的健康码(绿码)示意图,用黑白打印机打印于边长为 的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量反复实验,发现点落入黑色部分的频率稳定在 左右,据此可以估计黑色部分的总面积约为( )
 A、 B、 C、 D、6. 如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为120°,AB的长为30cm,贴纸部分BD的长为20cm,则贴纸部分的面积是( )
A、 B、 C、 D、6. 如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为120°,AB的长为30cm,贴纸部分BD的长为20cm,则贴纸部分的面积是( ) A、100πcm2 B、πcm2 C、πcm2 D、800πcm27. 若二次函数y=ax2(a≠0)的图象过点(﹣2,﹣3),则必在该图象上的点还有( )A、(﹣3,﹣2) B、(2,3) C、(2,﹣3) D、(﹣2,3)8. 如图,在⊙O中,= . 有下列结论:
A、100πcm2 B、πcm2 C、πcm2 D、800πcm27. 若二次函数y=ax2(a≠0)的图象过点(﹣2,﹣3),则必在该图象上的点还有( )A、(﹣3,﹣2) B、(2,3) C、(2,﹣3) D、(﹣2,3)8. 如图,在⊙O中,= . 有下列结论:
①AB=CD;②AC=BD;③∠AOC=∠BOD;④= .
其中正确的有( )
A、②③④ B、①②③④ C、①②④ D、①②③9. 如图,以O为位似中心且与ABC位似的图形编号是( )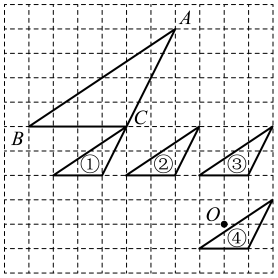 A、① B、② C、③ D、④10. 如图所示,在Rt△ABC中,∠C=90°,AC=6 cm,BC=2 cm,点P在边AC上,从点A向点C移动,点Q在边CB上,从点C向点B移动.若点P,Q均以1 cm/s的速度同时出发,且当一点移动到终点时,另一点也随之停止,连接PQ,则线段PQ的最小值是( )
A、① B、② C、③ D、④10. 如图所示,在Rt△ABC中,∠C=90°,AC=6 cm,BC=2 cm,点P在边AC上,从点A向点C移动,点Q在边CB上,从点C向点B移动.若点P,Q均以1 cm/s的速度同时出发,且当一点移动到终点时,另一点也随之停止,连接PQ,则线段PQ的最小值是( ) A、20 cm B、18 cm C、2 cm D、3 cm
A、20 cm B、18 cm C、2 cm D、3 cm二、填空题(每题5分,共30分)
-
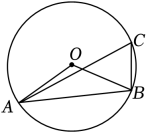
11. 明明家过年时包了100个饺子,其中有一个饺子中包有幸运果.明明任意挑选了一个饺子,正好是包有幸运果的饺子的概率是.12. 如图,A、B、C为⊙O上三点,若∠AOB=140°,则∠ACB度数为°.
 13. 如图,点 在 上,弦 垂直平分 ,垂足为 .若 ,则 的长为 .
13. 如图,点 在 上,弦 垂直平分 ,垂足为 .若 ,则 的长为 .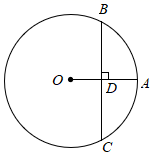 14. 如图,在中, , , 点M , N分别在边上,将沿直线翻折,点C恰好落在边上,记为点 , 如果与相似,那么折痕的长为 .
14. 如图,在中, , , 点M , N分别在边上,将沿直线翻折,点C恰好落在边上,记为点 , 如果与相似,那么折痕的长为 .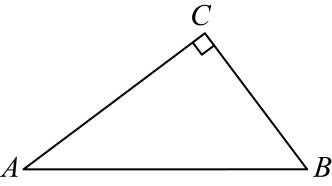 15. 如图,在中,点D是边上的一点, , , , 则边的长为 .
15. 如图,在中,点D是边上的一点, , , , 则边的长为 . 16. 如图所示,内接于半径为的半圆中,AB为直径,点是的中点,连结BM交AC于点E,AD平分交BM于点 , 且为BM的中点,则DM的长为 , BC的长为.
16. 如图所示,内接于半径为的半圆中,AB为直径,点是的中点,连结BM交AC于点E,AD平分交BM于点 , 且为BM的中点,则DM的长为 , BC的长为.
三、解答题
-
17. 在学校开展的数学活动课上,小明和小刚制作了一个正三棱锥(质量均匀,四个面完全相同),并在各个面上分别标记数字1,2,3,4,游戏规则如下:每人投掷三棱锥一次,并记录底面的数字,如果底面数字的和为奇数,那么小明赢;如果底面数字的和为偶数,那么小刚赢.
 (1)、请用列表或画树状图的方法表示上述游戏中的所有可能结果.(2)、请分别求出小明和小刚能赢的概率,并判断此游戏对双方是否公平.18. 如图,在的方格纸中,每个小正方形边长都是1,是格点三角形(顶点在方格顶点处).
(1)、请用列表或画树状图的方法表示上述游戏中的所有可能结果.(2)、请分别求出小明和小刚能赢的概率,并判断此游戏对双方是否公平.18. 如图,在的方格纸中,每个小正方形边长都是1,是格点三角形(顶点在方格顶点处). (1)、在图1中画格点 , 使与相似,相似比为.(2)、在图2中画格点 , 使与相似,面积比为.(注:图、图在答题纸上.)19. 某超市购进一批时令水果,成本为元千克,根据市场调研发现,这种水果在未来天的销售单价元千克与时间天之间的函数关系式为为整数 , 且其日销售量千克与时间天之间的函数关系如图所示:
(1)、在图1中画格点 , 使与相似,相似比为.(2)、在图2中画格点 , 使与相似,面积比为.(注:图、图在答题纸上.)19. 某超市购进一批时令水果,成本为元千克,根据市场调研发现,这种水果在未来天的销售单价元千克与时间天之间的函数关系式为为整数 , 且其日销售量千克与时间天之间的函数关系如图所示: (1)、求每天销售这种水果的利润元与天之间的函数关系式;(2)、问哪一天销售这种水果的利润最大?最大日销售利润为多少?20. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)、求每天销售这种水果的利润元与天之间的函数关系式;(2)、问哪一天销售这种水果的利润最大?最大日销售利润为多少?20. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B. (1)、求证:△ADF∽△DEC;(2)、若AB=8,AD=6 ,AF=4 ,求AE的长.21. 如图,在矩形ABCD中,AB=2,BC=4,E,F,G,H四点依次是边AB,BC,CD,DA上一点(不与各顶点重合),且AE=AH=CG=CF,记四边形EFGH面积为S(图中阴影),AE=x.
(1)、求证:△ADF∽△DEC;(2)、若AB=8,AD=6 ,AF=4 ,求AE的长.21. 如图,在矩形ABCD中,AB=2,BC=4,E,F,G,H四点依次是边AB,BC,CD,DA上一点(不与各顶点重合),且AE=AH=CG=CF,记四边形EFGH面积为S(图中阴影),AE=x.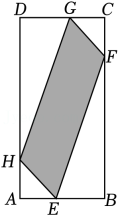 (1)、求S关于x的函数表达式,并直接写出自变量的取值范围.(2)、求x为何值时,S的值最大,并写出S的最大值.22. 如图,转盘的红色扇形和蓝色扇形的圆心角分别为和 , 转盘可以自由转动.
(1)、求S关于x的函数表达式,并直接写出自变量的取值范围.(2)、求x为何值时,S的值最大,并写出S的最大值.22. 如图,转盘的红色扇形和蓝色扇形的圆心角分别为和 , 转盘可以自由转动.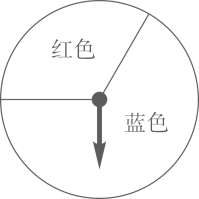 (1)、转动一次转盘,求指针落在红色扇形内的概率;(2)、转动两次转盘,利用树状图或者列表法分析指针两次都落在蓝色扇形内的概率.23. 请阅读下列材料,并完成相应的任务:阿基米德折弦定理,阿基米德(公元前287年一公元前212年),伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家,静态力学和流体静力学的奠基人,并且享有“力学之父”的美称,阿基米德和高斯,牛顿并列为世界三大数学家.
(1)、转动一次转盘,求指针落在红色扇形内的概率;(2)、转动两次转盘,利用树状图或者列表法分析指针两次都落在蓝色扇形内的概率.23. 请阅读下列材料,并完成相应的任务:阿基米德折弦定理,阿基米德(公元前287年一公元前212年),伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家,静态力学和流体静力学的奠基人,并且享有“力学之父”的美称,阿基米德和高斯,牛顿并列为世界三大数学家.阿拉伯Al-Binmi(973年一1050年)的译文中保存了阿基米德折弦定理的内容,苏联在1964年根据Al-Binmi译本出版了俄文版《阿基米德全集》,第一题就是阿基米德折弦定理.
阿基米德折弦定理:如图1,AB和BC是⊙O的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.
小明同学运用“截长法”和三角形全等来证明CD=AB+BD,过程如下:
证明:如图2所示,在CB上截取CG=AB,连接MA,MB,MC和MG.
∵M是的中点,∴MA=MC,…
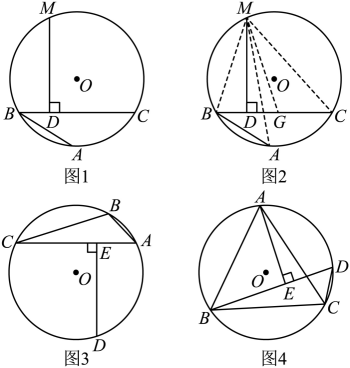 (1)、请按照上述思路,写出该证明的剩余部分;(2)、如图3,在⊙O中,BD =CD,DE⊥AC,若AB = 4,AC = 10,则AE的长度为;(3)、如图4,已知等边ABC内接于⊙O,AB = 8,D为上一点,∠ABD = 45°,AE⊥BD于点E,求BDC的周长.24. 在△ABC中,∠ACB=90°,AB=20,BC=12.
(1)、请按照上述思路,写出该证明的剩余部分;(2)、如图3,在⊙O中,BD =CD,DE⊥AC,若AB = 4,AC = 10,则AE的长度为;(3)、如图4,已知等边ABC内接于⊙O,AB = 8,D为上一点,∠ABD = 45°,AE⊥BD于点E,求BDC的周长.24. 在△ABC中,∠ACB=90°,AB=20,BC=12. (1)、如图1,折叠△ABC使点A落在AC边上的点D处,折痕交AC、AB分别于Q、H , 若S△ABC=9S△DHQ , 则HQ= .(2)、如图2,折叠△ABC使点A落在BC边上的点M处,折痕交AC、AB分别于E、F . 若FM∥AC , 求证:四边形AEFM是菱形;(3)、在(1)(2)的条件下,线段CQ上是否存在点P , 使得△CMP和△HQP相似?若存在,求出PQ的长;若不存在,请说明理由.(4)、在线段AC上找一点G , 使值最小,请直接写出最小值.
(1)、如图1,折叠△ABC使点A落在AC边上的点D处,折痕交AC、AB分别于Q、H , 若S△ABC=9S△DHQ , 则HQ= .(2)、如图2,折叠△ABC使点A落在BC边上的点M处,折痕交AC、AB分别于E、F . 若FM∥AC , 求证:四边形AEFM是菱形;(3)、在(1)(2)的条件下,线段CQ上是否存在点P , 使得△CMP和△HQP相似?若存在,求出PQ的长;若不存在,请说明理由.(4)、在线段AC上找一点G , 使值最小,请直接写出最小值.