2023-2024学年浙教版数学九年级(上)期末仿真模拟卷(三)(九上全册)
试卷更新日期:2023-12-22 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 下列函数y是x的二次函数的是( )A、y=2x+1 B、y=(x+1)2-x2 C、y=3x2+1 D、2. 在同一坐标系中,一次函数y=-mx+n2与二次函数y=x2+m的图象可能是( )A、
 B、
B、 C、
C、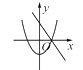 D、
D、 3. 在一个不透明的空袋子里,放入仅颜色不同的2个红球和1个白球,从中随机摸出1个球后不放回,再从中随机摸出1个球,两次都摸到红球的概率是( )A、 B、 C、 D、4. 在一个暗箱里放有a个除颜色外其它完全相同的球,这a个球中红球只有3个.每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在25%,那么可以推算出a大约是( )A、12 B、9 C、4 D、35. 如图△ABC中,∠C=90°,∠B=20°,以C为圆心,CA为半径的圆交AB于点D, 则的度数为( )
3. 在一个不透明的空袋子里,放入仅颜色不同的2个红球和1个白球,从中随机摸出1个球后不放回,再从中随机摸出1个球,两次都摸到红球的概率是( )A、 B、 C、 D、4. 在一个暗箱里放有a个除颜色外其它完全相同的球,这a个球中红球只有3个.每次将球搅拌均匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球实验后发现,摸到红球的频率稳定在25%,那么可以推算出a大约是( )A、12 B、9 C、4 D、35. 如图△ABC中,∠C=90°,∠B=20°,以C为圆心,CA为半径的圆交AB于点D, 则的度数为( )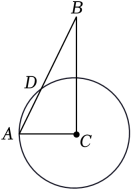 A、30° B、40° C、45° D、50°6. 如图所示,将等腰直角三角形ABC绕点A逆时针旋转15°得到 , 若 , 则图中阴影部分面积为( )
A、30° B、40° C、45° D、50°6. 如图所示,将等腰直角三角形ABC绕点A逆时针旋转15°得到 , 若 , 则图中阴影部分面积为( )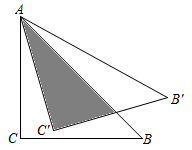 A、 B、 C、 D、7. 如图,AB为的直径,点D是的中点,过点D作于点E , 延长DE交于点F . 若 , , 则的直径长为( )
A、 B、 C、 D、7. 如图,AB为的直径,点D是的中点,过点D作于点E , 延长DE交于点F . 若 , , 则的直径长为( ) A、 B、8 C、10 D、8. 小明有一张上海市地图,地图的比例尺是 , 如果A , B两地在地图上的距离是4厘米,那么A , B两地的实际距离是( )A、8千米 B、0.8千米 C、0.08千米 D、0.008千米9. 如图,已知一组平行线 , 被直线m、n所截,交点分别为A、B、C和D、E、F,且AB=2,BC=4,DE=1.6,则EF=( )
A、 B、8 C、10 D、8. 小明有一张上海市地图,地图的比例尺是 , 如果A , B两地在地图上的距离是4厘米,那么A , B两地的实际距离是( )A、8千米 B、0.8千米 C、0.08千米 D、0.008千米9. 如图,已知一组平行线 , 被直线m、n所截,交点分别为A、B、C和D、E、F,且AB=2,BC=4,DE=1.6,则EF=( ) A、1.8 B、2.4 C、2.8 D、3.210. 在中, , 点是边上的一动点,过点作交边于点 , 过点作交的延长线于点 , 分别以为对角线画矩形和矩形 , 则在从到的运动过程中,当矩形和矩形的面积和最小时,则的长度为( )
A、1.8 B、2.4 C、2.8 D、3.210. 在中, , 点是边上的一动点,过点作交边于点 , 过点作交的延长线于点 , 分别以为对角线画矩形和矩形 , 则在从到的运动过程中,当矩形和矩形的面积和最小时,则的长度为( ) A、 B、 C、6 D、
A、 B、 C、6 D、二、填空题(每题4分,共24分)
-
11. 如图.二次函数y=ax2+bx+c的图象与x轴交于点(3,0),对称轴是直线上x= 1.则当y<0时。自变量x的取值范围是
 12. 如图,甲、乙、丙人站在网格中的三个格子中,小王随机站在剩下的空格中,与图中人均不在同一行或同一列的概率是 .
12. 如图,甲、乙、丙人站在网格中的三个格子中,小王随机站在剩下的空格中,与图中人均不在同一行或同一列的概率是 . 13. 兴隆蔬菜基地建圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m ,高度CD为 m.
13. 兴隆蔬菜基地建圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m ,高度CD为 m.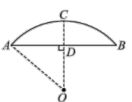 14. 如图,AB为△ADC的外接圆⊙O的直径,若∠BAD=50°,则∠ACD=°.
14. 如图,AB为△ADC的外接圆⊙O的直径,若∠BAD=50°,则∠ACD=°.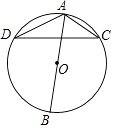 15. 如果两个相似三角形的相似比是2:3,那么它们的周长比是.16. 如图①,是一建筑物造型的纵截面,曲线OBA是抛物线的一部分,该抛物线开口向右、对称轴正好是水平线OH,AC,BD是与水平线OH垂直的两根支柱,AC=4米,BD=2米,OD=2米.
15. 如果两个相似三角形的相似比是2:3,那么它们的周长比是.16. 如图①,是一建筑物造型的纵截面,曲线OBA是抛物线的一部分,该抛物线开口向右、对称轴正好是水平线OH,AC,BD是与水平线OH垂直的两根支柱,AC=4米,BD=2米,OD=2米. (1)、如图②,为了安全美观,准备拆除支柱AC、BD,在水平线OH上另找一点P作为地面上的支撑点,用固定材料连接PA、PB,对抛物线造型进行支撑加固,用料最省时点O,P之间的距离是 .(2)、如图③,在水平线OH上增添一张2米长的椅子EF(E在F右侧),用固定材料连接AE、BF,对抛物线造型进行支撑加固,用料最省时点O,E之间的距离是 .
(1)、如图②,为了安全美观,准备拆除支柱AC、BD,在水平线OH上另找一点P作为地面上的支撑点,用固定材料连接PA、PB,对抛物线造型进行支撑加固,用料最省时点O,P之间的距离是 .(2)、如图③,在水平线OH上增添一张2米长的椅子EF(E在F右侧),用固定材料连接AE、BF,对抛物线造型进行支撑加固,用料最省时点O,E之间的距离是 .三、解答题(共8题,共66分)
-
17. 从长度分别为3 cm,5 cm,7 cm,x(cm) (x为整数)的四条线段中任取三条作为边,要使它们能组成三角形的概率为 , 则x的值应满足什么条件?18. 如图,一圆弧形桥拱的圆心为 ,拱桥的水面跨度 米,桥拱到水面的最大高度 为 米.求:
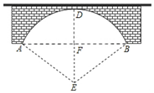 (1)、桥拱的半径;(2)、现水面上涨后水面跨度为 米,求水面上涨的高度为米.19. 如图,在平面直角坐标系中,过抛物线 的顶点A作x轴的平行线,交抛物线y=x2+1于点B , 点B在第一象限.
(1)、桥拱的半径;(2)、现水面上涨后水面跨度为 米,求水面上涨的高度为米.19. 如图,在平面直角坐标系中,过抛物线 的顶点A作x轴的平行线,交抛物线y=x2+1于点B , 点B在第一象限. (1)、求点A的坐标;(2)、点P为x轴上任意一点,连结AP、BP , 求△ABP的面积.20. 为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为 , 矩形区域ABCD的面积为.
(1)、求点A的坐标;(2)、点P为x轴上任意一点,连结AP、BP , 求△ABP的面积.20. 为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为 , 矩形区域ABCD的面积为. (1)、求与之间的函数表达式,并写出的取值范围.(2)、当为何值时,有最大值?最大值是多少?21. 某县为创评“全国文明城市”称号,周末团县委组织志愿者进行宣传活动.班主任周老师决定从4名女班干部(小兰,小红,小丽和小倩)中通过抽签方式确定2名女生去参加.抽签规则:将4名女班干部姓名分别写在4张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,周老师先从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.(1)、第一次抽取卡片“小红被抽中”的概率为;(2)、用画树状图或列表的方法表示这次抽签所有可能的结果,并求出“小丽被抽中”的概率.22. 在平面直角坐标系中,抛物线经过点 , , 其中 , 是方程的两点,且 , 过点A的直线与抛物线只有一个公共点.
(1)、求与之间的函数表达式,并写出的取值范围.(2)、当为何值时,有最大值?最大值是多少?21. 某县为创评“全国文明城市”称号,周末团县委组织志愿者进行宣传活动.班主任周老师决定从4名女班干部(小兰,小红,小丽和小倩)中通过抽签方式确定2名女生去参加.抽签规则:将4名女班干部姓名分别写在4张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,周老师先从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.(1)、第一次抽取卡片“小红被抽中”的概率为;(2)、用画树状图或列表的方法表示这次抽签所有可能的结果,并求出“小丽被抽中”的概率.22. 在平面直角坐标系中,抛物线经过点 , , 其中 , 是方程的两点,且 , 过点A的直线与抛物线只有一个公共点. (1)、求A,C两点的坐标:(2)、求直线的解析式;(3)、如图2,点B是线段(端点除外)上的动点,若过点B作轴的平行线与直线l相交于点E,与抛物线相交于点D,求的值.
(1)、求A,C两点的坐标:(2)、求直线的解析式;(3)、如图2,点B是线段(端点除外)上的动点,若过点B作轴的平行线与直线l相交于点E,与抛物线相交于点D,求的值.

