2023-2024学年浙教版数学九年级(上)期末仿真模拟卷(二)(九上全册)
试卷更新日期:2023-12-22 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 若线段 , , , 是成比例线段,且 , , ,则 ( )A、 B、 C、 D、2. 下列事件中,属于必然事件的是( )A、抛掷硬币时,正面朝上 B、小明发烧了,体温达到50℃ C、经过红绿灯路口,遇到红灯 D、任意写一个负数,小于正数3. 已知某抛物线与二次函数的图象的开口大小相同,开口方向相反,且顶点坐标为(1,2023),则该抛物线对应的函数表达式为( )A、 B、 C、 D、4. 已知⊙O的半径为2,点P在⊙O内,则OP的长可能是( )A、1 B、2 C、3 D、45. 一个不透明的盒子里有n个除颜色外其它完全相同的小球,其中有6个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后在放回盒子,通过大量重复摸球实验后发现,摸到黄球的频率稳定在30%,那么可以推算出n大约是( )A、6 B、10 C、18 D、206. 往直径为的圆柱形容器内装入一些水以后,截面如图所示,若水面的宽度为 , 则水的最大深度为( )
 A、 B、 C、 D、7. 二次函数y=ax2+bx+3(a≠0),当x=1和x=2016时函数的值相等,则当x=2017时,函数的值等于( )
A、 B、 C、 D、7. 二次函数y=ax2+bx+3(a≠0),当x=1和x=2016时函数的值相等,则当x=2017时,函数的值等于( )
A、 B、3 C、 D、-38. 如图,A、D是⊙O上的两个点,BC是直径,若∠D=32°,则∠OAC等于( ) A、64° B、58° C、68° D、55°9. 已知两个相似三角形的相似比为4:9,则它们周长的比为( )A、2:3 B、4:9 C、3:2 D、16:8110. 两个大小不一的五边形和五边形如图所示位置,点在线段上,点在线段上,对应连接并延长 , , 刚好交于一点 , 则这两个五边形的关系是( )
A、64° B、58° C、68° D、55°9. 已知两个相似三角形的相似比为4:9,则它们周长的比为( )A、2:3 B、4:9 C、3:2 D、16:8110. 两个大小不一的五边形和五边形如图所示位置,点在线段上,点在线段上,对应连接并延长 , , 刚好交于一点 , 则这两个五边形的关系是( ) A、一定相似 B、一定不相似 C、不一定相似 D、不能确定
A、一定相似 B、一定不相似 C、不一定相似 D、不能确定二、填空题(每题4分,共24分)
-
11. 如图,一抛物线型拱桥,当拱顶到水面的距离为2米时,水面宽度为4米;那么当水位下降1.5米后,水面的宽度为 米.
 12. 某啤酒厂举办促销活动,在一箱啤酒(24 瓶)中有4瓶的瓶盖内印有“奖”字,小明的爸爸买了一箱这种啤酒,但连续打开4瓶均未中奖,那么他打开下一瓶啤酒中奖的概率是.13. 如图,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,连接 ,若将 绕点 顺时针旋转 ,得到 ,则点 的坐标为 .
12. 某啤酒厂举办促销活动,在一箱啤酒(24 瓶)中有4瓶的瓶盖内印有“奖”字,小明的爸爸买了一箱这种啤酒,但连续打开4瓶均未中奖,那么他打开下一瓶啤酒中奖的概率是.13. 如图,在平面直角坐标系中,点 的坐标为 ,点 的坐标为 ,连接 ,若将 绕点 顺时针旋转 ,得到 ,则点 的坐标为 . 14. 剪纸是中国最古老的民间艺术之一.如图,这个剪纸图案绕着它的中心旋转角α (0°<α<360°)后能够与它本身完全重合.则角α可以为度(写出一个即可).
14. 剪纸是中国最古老的民间艺术之一.如图,这个剪纸图案绕着它的中心旋转角α (0°<α<360°)后能够与它本身完全重合.则角α可以为度(写出一个即可). 15. 一条弦把圆分为2:3两部分,那么这条弦所对的圆周角的度数为 .16. 如图,在矩形ABCD中,AB>AD,AN平分∠DAB,交DC于点E,DM⊥AN于点M,CN⊥AN于点N,G为MN的中点,GH⊥MN交CD于点H,且DM=m,GH=n.
15. 一条弦把圆分为2:3两部分,那么这条弦所对的圆周角的度数为 .16. 如图,在矩形ABCD中,AB>AD,AN平分∠DAB,交DC于点E,DM⊥AN于点M,CN⊥AN于点N,G为MN的中点,GH⊥MN交CD于点H,且DM=m,GH=n. (1)、∠DCN= .(2)、线段CN的长为 . (用含m,n的代数式表示)
(1)、∠DCN= .(2)、线段CN的长为 . (用含m,n的代数式表示)三、解答题(共8题,共66分)
-
17. 如图,四边形 四边形 .
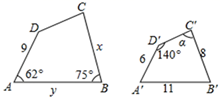 (1)、 = , 它们的相似比是.(2)、求边x、y的长度.18. 如图,四边形内接于 , 分别延长 , , 使它们相交于点 , , 且.
(1)、 = , 它们的相似比是.(2)、求边x、y的长度.18. 如图,四边形内接于 , 分别延长 , , 使它们相交于点 , , 且.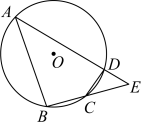 (1)、求证:.(2)、若 , 点为的中点,求的半径.19. 某中学运动队有短跑、长跑、跳远、实心球四个训练小队,现将四个训练小队队员情况绘制成如下不完整的统计图:
(1)、求证:.(2)、若 , 点为的中点,求的半径.19. 某中学运动队有短跑、长跑、跳远、实心球四个训练小队,现将四个训练小队队员情况绘制成如下不完整的统计图: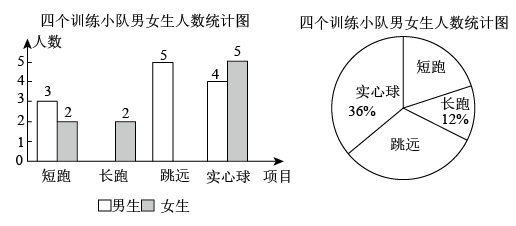 (1)、学校运动队的队员总人数为;(2)、补全条形统计图,并标明数据;(3)、若在长跑训练小组中随机选取2名同学进行比赛,请用列举法(画树状图或列表)求所选取的这两名同学恰好是一男一女的概率.20. 已知二次函数 .(1)、求该二次函数的图象与y轴交点的坐标及对称轴.(2)、已知点都在该二次函数图象上,
(1)、学校运动队的队员总人数为;(2)、补全条形统计图,并标明数据;(3)、若在长跑训练小组中随机选取2名同学进行比赛,请用列举法(画树状图或列表)求所选取的这两名同学恰好是一男一女的概率.20. 已知二次函数 .(1)、求该二次函数的图象与y轴交点的坐标及对称轴.(2)、已知点都在该二次函数图象上,①请判断与的大小关系: ▲ (用“”“”“”填空);
②若 , , , 四个函数值中有且只有一个小于零,求a的取值范围.
21. 如图,AB是半圆O的直径,C、D是半圆O上的两点,D为的中点,OD与AC交于点E. (1)、证明:(2)、若∠B=70°,求∠CAD的度数;(3)、若AB=4,AC=3,求DE的长.22. 在四边形中,为对角线, , 于点E, , .
(1)、证明:(2)、若∠B=70°,求∠CAD的度数;(3)、若AB=4,AC=3,求DE的长.22. 在四边形中,为对角线, , 于点E, , . (1)、如图1,求证:;(2)、如图2,延长 , 交边的延长线于点F,交边于点G,连接 , 在不添加任何字母和辅助线的条件下,请直接写出图中与相似,但不全等的三角形.23. 我们不妨约定:在平面直角坐标系中,若某直线l经过抛物线L:y=ax2+bx+c(a , b , c是常数,a≠0)的顶点和该抛物线与y轴的交点,则把该直线l称为抛物线L的“心心相融线”.根据该约定,请完成下列各题:(1)、若直线y=kx+1是抛物线y=x2-2x+1的“心心相融线”,求k的值.(2)、若过原点的抛物线L:y=-x2+bx+c(b , c是常数,且b≠0)的“心心相融线”为y=mx+n(m≠0),则代数式是否为定值?若是,请求出该定值;若不是,请说明理由.(3)、当常数k满足<k≤2时,求抛物线L:y=ax2+(3k2-2k+1)x+k(a , b , c是常数,a≠0)的“心心相融线”l与x轴,y轴所围成的三角形面积的取值范围.24. 在矩形中, , .点是边上的一点(与端点、不重合)
(1)、如图1,求证:;(2)、如图2,延长 , 交边的延长线于点F,交边于点G,连接 , 在不添加任何字母和辅助线的条件下,请直接写出图中与相似,但不全等的三角形.23. 我们不妨约定:在平面直角坐标系中,若某直线l经过抛物线L:y=ax2+bx+c(a , b , c是常数,a≠0)的顶点和该抛物线与y轴的交点,则把该直线l称为抛物线L的“心心相融线”.根据该约定,请完成下列各题:(1)、若直线y=kx+1是抛物线y=x2-2x+1的“心心相融线”,求k的值.(2)、若过原点的抛物线L:y=-x2+bx+c(b , c是常数,且b≠0)的“心心相融线”为y=mx+n(m≠0),则代数式是否为定值?若是,请求出该定值;若不是,请说明理由.(3)、当常数k满足<k≤2时,求抛物线L:y=ax2+(3k2-2k+1)x+k(a , b , c是常数,a≠0)的“心心相融线”l与x轴,y轴所围成的三角形面积的取值范围.24. 在矩形中, , .点是边上的一点(与端点、不重合) (1)、如图1,当时,联结交于点 , 求线段的长度;(2)、如图2,当时,求四边形的面积;(3)、如图3,过点作的垂线,交边于点 , 交于点.设 , , 求关于的函数关系式,并写出定义域.
(1)、如图1,当时,联结交于点 , 求线段的长度;(2)、如图2,当时,求四边形的面积;(3)、如图3,过点作的垂线,交边于点 , 交于点.设 , , 求关于的函数关系式,并写出定义域.