2023-2024学年浙教版数学九年级(上)期末仿真模拟卷(杭州适用2,九上全册)
试卷更新日期:2023-12-22 类型:期末考试
一、选择题(每题3分,共30分)
-
1. a,b,c,d是成比例线段,其中 , , ,则线段d为( )A、1cm B、2cm C、4cm D、9cm2. 下列事件中,属于必然事件的是( )A、小明买彩票中奖 B、任意抛掷一只纸杯,杯口朝下 C、任选三角形的两边,其差小于第三边 D、在一个没有红球的盒子里摸球,摸到了红球3. 将抛物线y=2x2平移,得到抛物线y=2(x+4)2+1,下列平移正确的是( )A、先向左平移4个单位,再向上平移1个单位 B、先向左平移4个单位,再向下平移1个单位 C、先向右平移4个单位,再向上平移1个单位 D、先向右平移4个单位,再向下平移1个单位4. 如图,四边形ABCD是⊙O的内接四边形,若∠AOC=160°,则∠ABC的度数是( )
 A、80° B、100° C、140° D、160°5. 将二次函数y=﹣x2+2x+3的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线y=x+b与新函数的图象恰有3个公共点时,b的值为( )
A、80° B、100° C、140° D、160°5. 将二次函数y=﹣x2+2x+3的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线y=x+b与新函数的图象恰有3个公共点时,b的值为( )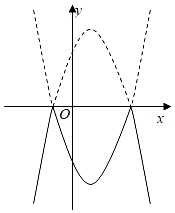 A、 或﹣3 B、 或﹣3 C、 或﹣3 D、 或﹣36. 不透明的口袋中装有3个黄球、1个红球和n个蓝球,这些小球除颜色外其余均相同,课外兴趣小组每次摸出一个球记录下颜色后再放回,大量重复试验后发现,摸到蓝球的频率稳定在0.6,则n的值最可能是( )A、4 B、5 C、6 D、77. 已知⊙O的半径为3,点P到圆心O的距离为4,则点P与⊙O的位置关系是( )A、点P在⊙O外 B、点P在⊙O上 C、点P在⊙O内 D、无法确定8. 如图,AB是⊙O的直径,C,D是⊙O上的两点,且BC平分∠ABD,AD分别与BC,OC相交于点E,F,则下列结论不一定成立的是( )
A、 或﹣3 B、 或﹣3 C、 或﹣3 D、 或﹣36. 不透明的口袋中装有3个黄球、1个红球和n个蓝球,这些小球除颜色外其余均相同,课外兴趣小组每次摸出一个球记录下颜色后再放回,大量重复试验后发现,摸到蓝球的频率稳定在0.6,则n的值最可能是( )A、4 B、5 C、6 D、77. 已知⊙O的半径为3,点P到圆心O的距离为4,则点P与⊙O的位置关系是( )A、点P在⊙O外 B、点P在⊙O上 C、点P在⊙O内 D、无法确定8. 如图,AB是⊙O的直径,C,D是⊙O上的两点,且BC平分∠ABD,AD分别与BC,OC相交于点E,F,则下列结论不一定成立的是( ) A、OC∥BD B、AD⊥OC C、△CEF≌△BED D、AF=FD9. 如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A、OC∥BD B、AD⊥OC C、△CEF≌△BED D、AF=FD9. 如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( ) A、
A、 B、
B、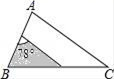 C、
C、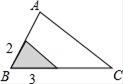 D、
D、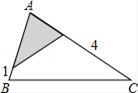 10. 如图,E,F,G,H分别是矩形四条边上的点,连接相交于点I,且 , , 矩形矩形 , 连接交于点P,Q,下列一定能求出面积的条件是( )
10. 如图,E,F,G,H分别是矩形四条边上的点,连接相交于点I,且 , , 矩形矩形 , 连接交于点P,Q,下列一定能求出面积的条件是( )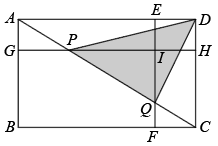 A、矩形和矩形的面积之差 B、矩形与矩形的面积之差 C、矩形和矩形的面积之差 D、矩形和矩形的面积之差
A、矩形和矩形的面积之差 B、矩形与矩形的面积之差 C、矩形和矩形的面积之差 D、矩形和矩形的面积之差二、填空题(每题4分,共24分)
-
11. 在中, , 那么它的重心G到C点距离是.12. 填空:(1)、小亮在篮球训练中,对多次投篮的数据进行记录,得到如下频数表:
投篮次数
20
40
60
80
120
160
200
投中次数
15
33
49
63
97
126
160
投中的频率
0.75
0.83
0.82
0.79
0.81
0.79
0.8
估计小亮投一次篮,投中的概率是.
(2)、小明抛掷硬币,第一次正面朝上.因为抛掷均匀的硬币,出现正面朝上的频率是50%,所以第二次一定反面朝上.这个说法(在横线上填“正确”或“错误”).13. 已知的半径为2,等边三角形ABC内接于 , 则的边长为 , 面积为.14. 已知两个相似三角形的一组对应边长分别是14和9,如果它们的周长相差20,那么较大三角形的周长为 .15. 如图,扇形AOB中,OA=10,∠AOB=36°.若将此扇形绕点B顺时针旋转,得一新扇形A′O′B,其中A点在O′B上,则点O的运动路径长为cm.(结果保留π) 16. 已知:如图,在平面直角坐标系xOy中,点A在抛物线上运动,过点A作AC⊥x轴于点C,以AC为对角线作正方形ABCD.则抛物线的顶点坐标是 , 正方形ABCD周长的最小值是 .
16. 已知:如图,在平面直角坐标系xOy中,点A在抛物线上运动,过点A作AC⊥x轴于点C,以AC为对角线作正方形ABCD.则抛物线的顶点坐标是 , 正方形ABCD周长的最小值是 .
三、解答题(共7题,共66分)
-
17. 在平面直角坐标系中,二次函数的对称轴为 , 且它经过点 , 求该二次函数的解析式和顶点坐标.18.
在一个不透明的盒子里装有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是“摸到白色球”的频率折线统计图.
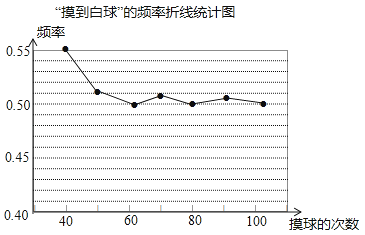 (1)、请估计:当n很大时,摸到白球的概率将会接近 (精确到0.01),假如你摸一次,你摸到白球的概率为(2)、试估算盒子里白、黑两种颜色的球各有多少个?(3)、在(2)条件下如果要使摸到白球的概率为 , 需要往盒子里再放入多少个白球?19. 如图,⊙O的直径AB垂直于弦CD,垂足为E,AE=2,CD=8.
(1)、请估计:当n很大时,摸到白球的概率将会接近 (精确到0.01),假如你摸一次,你摸到白球的概率为(2)、试估算盒子里白、黑两种颜色的球各有多少个?(3)、在(2)条件下如果要使摸到白球的概率为 , 需要往盒子里再放入多少个白球?19. 如图,⊙O的直径AB垂直于弦CD,垂足为E,AE=2,CD=8. (1)、求⊙O的半径长;(2)、连接BC,作OF⊥BC于点F,求OF的长.20. 如图,在中, , 点D在上, , 过点B作 , 交的延长线于点E.
(1)、求⊙O的半径长;(2)、连接BC,作OF⊥BC于点F,求OF的长.20. 如图,在中, , 点D在上, , 过点B作 , 交的延长线于点E. (1)、求证:;(2)、如果 , , 求的长.21. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答下列问题.
(1)、求证:;(2)、如果 , , 求的长.21. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答下列问题. (1)、写出方程ax2+bx+c=0的根;(2)、写出不等式ax2+bx+c<0的解集;(3)、若方程ax2+bx+c=k无实数根,写出k的取值范围.22. 如图,内接于 , , 的外角的平分线交于点D,连接 , , 交于点F.
(1)、写出方程ax2+bx+c=0的根;(2)、写出不等式ax2+bx+c<0的解集;(3)、若方程ax2+bx+c=k无实数根,写出k的取值范围.22. 如图,内接于 , , 的外角的平分线交于点D,连接 , , 交于点F. (1)、求证:是等腰三角形.(2)、若.
(1)、求证:是等腰三角形.(2)、若.①求证:.
②若的半径为5, , 求的值.
23. 数学活动课上,老师给出这样一个题目:如图1,点C是弧上的点,于D,于E,若 , 求证:点C是弧的中点.小波同学想到的办法是:可通过证明来完成它.
 (1)、请你们帮助小波完成证明过程:(2)、解答完老师给出的问题后,小波把老师的题进行了改变.
(1)、请你们帮助小波完成证明过程:(2)、解答完老师给出的问题后,小波把老师的题进行了改变.如图2,已知是的直径,点D,点E分别是半径 , 的中点,延长交于点F,若于D,且点C是弧的中点,求证: , 请你证明.
(3)、拓展:如图3,在(2)的条件下,点G是弧上一点,连接 , , 若 , , 求的半径长.