2023~2024学年沪科版九年级上册期末数学质量评估卷【二】
试卷更新日期:2023-12-21 类型:期末考试
一、选择题
-
1. 下列图形既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知(a、b、c、d都不为0),则下列各式一定成立的是( )A、 B、 C、 D、3. 下列函数中,y是x的反比例函数的是( )A、 B、 C、y=-2x D、4. 已知在中, , , , 那么下列等式正确的是( )A、 B、 C、 D、5. 若抛物线的顶点在第二象限,则m的取值范围是( )A、 B、 C、 D、6. 如图所示,是的边AC上一点,连结BP.下列条件中,不能判定的是( ).
2. 已知(a、b、c、d都不为0),则下列各式一定成立的是( )A、 B、 C、 D、3. 下列函数中,y是x的反比例函数的是( )A、 B、 C、y=-2x D、4. 已知在中, , , , 那么下列等式正确的是( )A、 B、 C、 D、5. 若抛物线的顶点在第二象限,则m的取值范围是( )A、 B、 C、 D、6. 如图所示,是的边AC上一点,连结BP.下列条件中,不能判定的是( ). A、 B、 C、 D、7. 如图,坡角为的斜坡上有一棵大树(垂直于水平地面),当太阳光线与水平线成角沿斜坡照下时,在斜坡上树影的长为30米,则大树的高为( )
A、 B、 C、 D、7. 如图,坡角为的斜坡上有一棵大树(垂直于水平地面),当太阳光线与水平线成角沿斜坡照下时,在斜坡上树影的长为30米,则大树的高为( )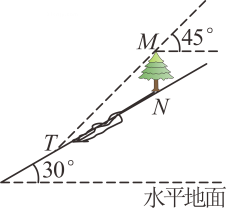 A、米 B、米 C、米 D、米8. 如图,为圆O的直径,C为圆O上一点,过点C作圆O的切线交的延长线于点D, , 连接 , 若 , 则的长度为( )
A、米 B、米 C、米 D、米8. 如图,为圆O的直径,C为圆O上一点,过点C作圆O的切线交的延长线于点D, , 连接 , 若 , 则的长度为( ) A、 B、 C、 D、9. 王刚在练习投篮,篮球脱手后的运动轨迹近似为如图所示的抛物线 , 已知篮圈高米,王刚投篮时出手高度为米,若要使篮球刚好投进篮圈C,则投篮时王刚离篮圈中心的水平距离为( )
A、 B、 C、 D、9. 王刚在练习投篮,篮球脱手后的运动轨迹近似为如图所示的抛物线 , 已知篮圈高米,王刚投篮时出手高度为米,若要使篮球刚好投进篮圈C,则投篮时王刚离篮圈中心的水平距离为( ) A、米 B、米 C、米 D、米10. 如图,在△ABC中,AB=13cm,AC=12cm,BC=5cm.D是BC边上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE,在点D变化的过程中,线段BE的最小值是( )
A、米 B、米 C、米 D、米10. 如图,在△ABC中,AB=13cm,AC=12cm,BC=5cm.D是BC边上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE,在点D变化的过程中,线段BE的最小值是( ) A、2.5 B、 C、 D、5
A、2.5 B、 C、 D、5二、填空题
-
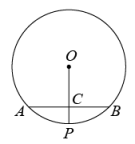
11. 已知二次函数的图像经过原点,那么m的值为 .12. 如图,的弦 , 过点O作于点C,交于点P,若 , 则的半径为.
 13. 如图,在平面直角坐标系中,点在第二象限,连接 , 过点作轴于点 , 反比例函数的图象分别与、交于点、 , 连接 , 若为的中点,且四边形的面积为 , 则的值为 .
13. 如图,在平面直角坐标系中,点在第二象限,连接 , 过点作轴于点 , 反比例函数的图象分别与、交于点、 , 连接 , 若为的中点,且四边形的面积为 , 则的值为 . 14. 如图,在直角三角形纸片中, , , , 点在边上,以为折痕将折叠得到 , 与边交于点 , 当时,的长是 .
14. 如图,在直角三角形纸片中, , , , 点在边上,以为折痕将折叠得到 , 与边交于点 , 当时,的长是 .
三、计算题
-
15. .
四、作图题
-
16. 如图,在平面直角坐标系中,已知 的三个顶点坐标分别是 , , .
 (1)、请作出 绕 点逆时针旋转 的 ;(2)、以点 为位似中心,将 扩大为原来的2倍,得到 ,请在 轴的左侧画出 ;(3)、请求出 的正弦值.
(1)、请作出 绕 点逆时针旋转 的 ;(2)、以点 为位似中心,将 扩大为原来的2倍,得到 ,请在 轴的左侧画出 ;(3)、请求出 的正弦值.五、解答题
-
17. 如图,直线y=kx+b与双曲线相交于A(﹣3,1),B两点,与x轴相交于点C(﹣4,0).
 (1)、分别求一次函数与反比例函数的解析式;(2)、连接OA,OB,求△AOB的面积;(3)、直接写出当x<0时,关于x的不等式的解集.18. 如图,在平行四边形中,过点A作 , 垂足为E,连接 , F为线段上一点,且.
(1)、分别求一次函数与反比例函数的解析式;(2)、连接OA,OB,求△AOB的面积;(3)、直接写出当x<0时,关于x的不等式的解集.18. 如图,在平行四边形中,过点A作 , 垂足为E,连接 , F为线段上一点,且. (1)、求证:;(2)、若 , , , 求的长.
(1)、求证:;(2)、若 , , , 求的长.六、综合题
-
19. 如图,某防洪指挥部发现长江边一处长200米,高10米,背水坡的坡角为的防洪大堤(横断面为梯形)急需加固.经调查论证,防洪指挥部专家组制定的加固方案:沿背水坡面用混泥土进行加固,加固后背水坡的坡比.
 (1)、求加固后坝底增加的宽度;(结果保留根号)(2)、求完成这项工程需要多少方混泥土?(结果精确到1立方米,)20. 已知二次函数y=ax2+bx-3中的x,y满足下表:
(1)、求加固后坝底增加的宽度;(结果保留根号)(2)、求完成这项工程需要多少方混泥土?(结果精确到1立方米,)20. 已知二次函数y=ax2+bx-3中的x,y满足下表:x
-1
0
1
2
3
y
0
-3
-4
-3
m
(1)、求这个二次函数的解析式:(2)、m= ;该函数图象与x轴的交点的坐标。(3)、当y>0时,x的取值范围。21. 如图,点是边上的一点,以为直径的交边、于点、.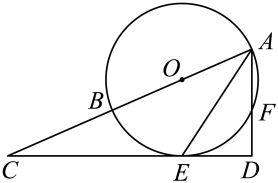
给出下列信息:
①平分;
②;
③直线是的切线.
(1)、请在上述条信息中,选择其中两条作为条件,其余的一条信息作为结论,组成一个真命题.你选择的条件是 ▲ 、 ▲ , 结论是 ▲ (只要填写序号),并说明理由.(2)、在(1)的情况下,若的半径为 , , 求的长.
-
-
 备用图
备用图
