浙江省杭州市瑞安西部六校2023年七年级上学期数学12月作业评价

试卷更新日期：2023-12-21 类型：月考试卷

进入出卷网下载

一、选择题(本题有10小题,每小题3分,共30分,每小题仅一个正确选项,多选、错选、不选均不给分)

1. 2023的相反数是（）

A、 $- \frac{1}{2023}$ B、 $\frac{1}{2023}$ C、-2023 D、2023

查看试题解析
2. 2023年9月23日，第19届亚运会在杭州开幕．据报道，开幕式的跨媒体阅读播放量达到503000000次，将503000000用科学记数法表示为（）

A、 $503 \times 1 0^{6}$ B、 $5.03 \times 1 0^{8}$ C、 $5.03 \times 1 0^{9}$ D、 $0.503 \times 1 0^{9}$

查看试题解析
3. 下列各数中，无理数是（）

A、 $\frac{π}{2}$ B、 $0 . \dot{5}$ C、 $\frac{22}{3}$ D、3.121121121112

查看试题解析
4. 下列关于单项式 $- \frac{2 x^{2} y}{3}$ 的说法中，正确的是（）

A、系数是 $- \frac{2}{3}$ ，次数是2 B、系数是 $\frac{2}{3}$ ，次数是2 C、系数是-2，次数是3 D、系数是 $- \frac{2}{3}$ ，次数是3

查看试题解析
5. 下列整式中与 $a^{2} b$ 是同类项的为（）

A、 $a b^{2}$ B、 $- a^{2} b$ C、 $2 a b$ D、 $a^{2} b c$

查看试题解析
6. 下列各式去括号正确的是（）

A、 $- (a - 3 b) = - a - 3 b$ B、 $a + (5 a - 3 b) = a + 5 a - 3 b$ C、 $- 2 (x - y) = - 2 x - 2 y$ D、 $- y + 3 (y - 2 x) = - y + 3 y - 2 x$

查看试题解析
7. 下列代数式中符合书写要求的是（）

A、 $a b^{2} \times 4$ B、 $6 x y^{2} \div 3$ C、 $2 \frac{1}{2} a^{2}$ D、 $\frac{1}{4} x$

查看试题解析
8. 在解方程 $\frac{x - 1}{2} - \frac{2 x + 3}{3} = 1$ 时，去分母正确的是（）

A、 $3 (x - 1) - 2 (2 x + 3) = 1$ B、 $3 (x - 1) + 2 (2 x + 3) = 1$ C、 $3 (x - 1) + 2 (2 x + 3) = 6$ D、 $3 (x - 1) - 2 (2 x + 3) = 6$

查看试题解析
9. 整式 $m x + 2 n$ 的值随 $x$ 的取值不同而不同，下表是当 $x$ 取不同值时整式 $m x + 2 n$ 对应的值，则关于 $x$ 的方程 $- 2 m x - 4 n = 4$ 的解为（）
x
-3
-2
-1
0
1
2
$m x + 2 n$
4
2
0
-2
-4
-6

A、 $x = - 3$ B、 $x = - 2$ C、 $x = 0$ D、 $x = 1$

查看试题解析
10. 如图，将图1中的长方形纸片剪成①号、②号、③号、④号正方形和⑤号长方形，并将它们按图2的方式无重叠地放入另一个大长方形中，若需求出没有覆盖的阴影部分的周长，则下列说法中错误的是（）

A、只需知道图1大长方形的周长即可 B、只需知道图2大长方形的周长即可 C、只需知道③号正方形的周长即可 D、只需知道⑤号长方形的周长即可

查看试题解析

二、填空题(本题有8小题,每小题3分,共24分)

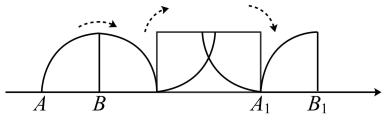
11. 中国人很早开始使用负数，中国古代数学著作《九章算术》的“方程”一章，在世界数学史上首次正式引入负数.如果收入100元记作+100元，那么支出80元记作元.

查看试题解析
12. 比较大小： $\sqrt{31}$ 6．（填“ $>$ ”、“ $=$ ”或“ $<$ ”）

查看试题解析
13. $\sqrt{9}$ 的平方根是

查看试题解析
14. 一个实数的两个平方根分别是 $a + 3$ 和 $2 a - 9$ ，则 $a =$ .

查看试题解析
15. 计算 $- \frac{1}{2} a b^{2} - 3 a b^{2} =$ .

查看试题解析
16. 某班46名同学去公园划船，一共乘坐10艘船.已知每条大船坐6人，每条小船坐4人，正好全部坐满.设大船有 $x$ 条，可列方程.

查看试题解析
17. 定义新运算：对于任意有理数a，b，都有 $a \oplus b = \frac{1}{2} (| a - b | + a + b)$ ，例如 $4 \oplus 2 = \frac{1}{2} (| 4 - 2 | + 4 + 2) = 4$ .将 $1 ， 2 ， 3 ， 4 ， ⋯ ， 50$ 这50个自然数分成25组，每组2个数，进行 $a \oplus b$ 运算，得到25个结果，则这25个结果的和的最大值是.

查看试题解析
18. 如图，在数轴上有一个四分之一圆，其半径的两个端点与数轴上的A、B两点重合，点A、B表示的数分别为a、b，满足 $\sqrt{a + 9} + | b - 7 | = 0$ ，则点 $A$ 表示的数为；图形从B点沿数轴向右无滑动滚动一周，圆上一点从 $A$ 点到达 $A_{1}$ 点处，则 $A_{1}$ 表示的数为.(结果保留 $π$ )

查看试题解析

三、解答题(本题有6小题,共46分.解答需写出必要的文字说明,演算步骤或证明过程)

19. 计算：

(1)、 $13 + (- 5) - (- 21) - 19$ ；

(2)、 $- 3^{2} + | - 2 | + \sqrt[3]{- 8}$ .

查看试题解析
20. 解方程：

(1)、 $4 - 3 (10 - x) = 5 x$ .

(2)、 $\frac{x + 1}{2} - \frac{2 - 3 x}{3} = 1$ .

查看试题解析
21. 先化简，再求值： $(3 x^{2} + x y + 2 y) - 2 (5 x y - 4 x^{2} + y)$ ，其中 $x = - 1 ， y = - \frac{1}{3}$ .

查看试题解析
22. 某巡警车在一条东西走向的大道上巡逻，某天巡警车从岗享0处出发，规定向东方向为正，当天行驶记录如下：(单位：千米) $+ 10 ， - 9 ， + 7 ， - 15 ， + 6 ， - 5 ， + 4 ， - 2$ .

(1)、最终巡警车是否回到岗亭0处?若没有，在岗亭何方，距岗亭多远?

(2)、巡警车行驶1千米耗油0.2升，油箱有油10升，够不够?若不够，途中至少还需补充多少升油?

查看试题解析

23.

如何设计班级菜地?
素材1	如图1是长方形菜园，长5m，宽3m. (1)中间种植区域是长方形，且长是宽的2倍. (2)四周过道部分的宽度相等
素材2	如图2，为了实现6个小组种植区域均匀分配，现将种植区域分割成大小相等的6垄长方形菜地，垄与垄之间的间距相等
素材3	每垄菜地的长比宽多30cm.

问题解决
任务1	分析数量关系	设过道宽度为x(m)，用含x的代数式表示种植区域的长与宽.
任务2	确定过道宽度	求过道宽度x的值
任务3	确定每垄菜地的大小	求每垄菜地的长与宽

查看试题解析

24. 如图，面积为30的长方形 $O A B C$ 的边 $O A$ 在数轴上， $O$ 为原点， $O C = 5$ .线段 $O_{1} C_{1}$ 从OC出发，以每秒1个单位的速度向右移动，与此同时线段 $A_{1} B_{1}$ 从 $A B$ 出发以每秒2个单位的速度向左移动.连结 $B_{1} C_{1}$ ，新长方形 $O_{1} A_{1} B_{1} C_{1}$ 与原长方形 $O A B C$ 重叠部分的面积记为 $S$ ，设运动时间为 $t$ .

(1)、当 $A_{1}$ 在O、A之间，用含 $t$ 的代数式表示 $O A_{1}$ ：.

(2)、 $S$ 恰好等于原长方形面积的一半时，数轴上点 $A_{1}$ 表示的数是多少?

(3)、长方形 $O_{1} A_{1} B_{1} C_{1}$ 与长方形 $O A B C$ 未重叠部分的面积记为 $S^{^{'}}$ ，请直接写出 $S^{^{'}} = 3 S$ 时， $t$ 的值.

查看试题解析