浙江省杭州市瑞安西部六校2023-2024学年八年级上学期数学12月作业评价

试卷更新日期：2023-12-21 类型：月考试卷

进入出卷网下载

一、选择题(本题共10小题,每小题3分,共30分.每小题只有一个选项是正确的,不选、多选、错选,均不给分)

1. 下列图案中，轴对称图形是（）

A、 B、 C、 D、

查看试题解析
2. 给定的三条线段中，不能组成三角形的是（）

A、4，4，9 B、3，5，6 C、6，8，10 D、5，12，13

查看试题解析
3. 下列各点中，位于第三象限的是（）

A、 $(2 ， 3)$ B、 $(- 1 ， - 4)$ C、 $(- 4 ， 1)$ D、 $(5 ， - 3)$

查看试题解析
4. 若 $x < y$ ，则下列不等式成立的是（）

A、 $x + 1 > y + 1$ B、 $2 x > 2 y$ C、 $- x > - y$ D、 $\frac{x}{3} > \frac{y}{3}$

查看试题解析
5. 下列选项中，能说明命题“对于任何实数 $a$ ，都有 $| a | > - a$ ”是假命题的反例是（）

A、 $a = \frac{1}{2}$ B、 $a = 1$ C、 $a = 2$ D、 $a = - 2$

查看试题解析
6. 函数 $y = \frac{x}{x + 1}$ 的自变量 $x$ 的取值范围为（）

A、 $x > - 1$ B、 $x < - 1$ C、 $x \neq - 1$ D、 $x \neq 0$

查看试题解析
7. 如图，两根竹竿AB和BD斜靠在墙上，量得 $∠ C A B ， ∠ C D B$ 的度数分别为 $3 8^{°}$ 和 $2 6^{°}$ ，那么 $∠ A B D$ 的度数为（）

A、 $1 0^{°}$ B、 $1 1^{°}$ C、 $1 2^{°}$ D、 $1 3^{°}$

查看试题解析
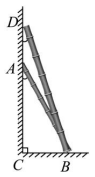8. 如图， $△ A B C$ 中， $A B < A C < B C$ ，如果要使用尺规作图的方法在BC上确定一点 $P$ ，使 $P A + P B =$ BC，那么符合要求的作图痕迹是（）

A、 B、 C、 D、

查看试题解析
9. 已知关于x的不等式 $2 x + a ⩽ 1$ 只有两个正整数解，则 $a$ 的取值范围为（）

A、 $- 5 < a < - 3$ B、 $- 5 ⩽ a < - 3$ C、 $- 5 < a ⩽ - 3$ D、 $- 5 ⩽ a ⩽ - 3$

查看试题解析
10. 在图1所示的 $3 \times 3$ 的网格内有一个八边形，其中每个小方格的边长均为1.经探究发现，此八边形可按图2的方式分割成四个全等的五边形和一个小正方形①.现将分割后的四个五边形重新拼接(即图2中的阴影部分)，得到一个大正方形ABCD，发现该正方形中间的空白部分②也是个正方形，记正方形①得面积为S₁ ，正方形②的面积为S₂ ，且 $S_{1} ： S_{2} = 3 ： 2$ ，则大正方形ABCD的边长为（）

A、 $\sqrt{3}$ B、2 C、 $\sqrt{5}$ D、 $\sqrt{6}$

查看试题解析

二、填空题(本题共8小题,每小题3分,共24分)

11. 用不等式表示“ $a$ 的2倍与1的和是正数”：.

查看试题解析
12. 在 $△ A B C$ 中， $A B = A C ， ∠ B = 4 0^{°}$ ，则 $∠ C$ 的度数是度.

查看试题解析
13. 在平面直角坐标系中，点 $(3 ， - 5)$ 到 $y$ 轴的距离是

查看试题解析
14. 如图是在固定的电压下，一电阻的阻值 $R (Ω)$ 与通过该电阻的电流 $I (A)$ 之间的函数关系图.根据图象，当自变量 $I = 2 (A)$ 时，函数值为.

查看试题解析
15. 某业主贷款22000元购进一台机器，生产某种产品.已知产品的成本每个5元，售价是每个8元.若每月能生产、销售2000个产品，问至少个月后能赚回这台机器的贷款.

查看试题解析
16. 如图，在平面直角坐标系中，直线 $l$ 是一、三象限的角平分线，点 $P$ 是直线 $l$ 上的一个动点， $A (3 ， 0) ， B (6 ， 0)$ 是 $x$ 轴上的两个点，则 $P A + P B$ 的最小值为.

查看试题解析
17. 如图， $∠ A O B = 3 0^{°}$ ，点 $D$ 为 $∠ A O B$ 平分线OC上一点，OD的垂直平分线交OA，OB分别于点P，Q，点 $E$ 是OA上异于点 $P$ 的一点，且 $D E = O P = 2$ ，则 $△ O D E$ 的面积为.

查看试题解析
18. 如图是一个提供床底收纳支持的气压伸缩杆，除了AB是完全固定的钢架外，AD，BC，DE属于位置可变的定长钢架.如图1所示， $A B = 29 c m ， A D = 13 c m ， B C = 20 c m$ ，伸缩杆PQ的两端分别固定在BC，CE两边上，其中 $P B = 13 c m ， C Q = 20 c m$ .当伸缩杆PQ打开最大时，如图2所示， $∠ A D C$ 成 $18 0^{°}$ ，此时 $P Q = \sqrt{449} c m$ ，则可变定长钢架CD的长度为 $c m$ .当伸缩杆完全收拢时， $C D / / A B$ ，则此时床高(CD与AB之间的距离）为cm.

查看试题解析

三、解答题（本题有6小题，共46分）

19. 解下列不等式（组）.

(1)、4x-2<1-2x

(2)、 ${\begin{array}{l} 3 - 2 x \geq x - 6 \\ \frac{3 x + 1}{2} < 2 x \end{array}$

查看试题解析
20. 如图，已知AB=DC，AC=DB．求证：∠A=∠D．
下面是两位同学的对话：
方方说：根据条件，找不到全等三角形．
圆圆说：如果添加辅助线，就可以找到全等三角形了．
请根据提示给出证明．

查看试题解析
21. 如图所示，在平面直角坐标系中，点 $O$ 为坐标原点，点 $A$ 的坐标为 $(2 ， 3)$ .

(1)、将点 $A$ 向右平移1个单位，向下平移2个单位所得的点 $B$ 的坐标为；

(2)、点 $A$ 关于 $y$ 轴的对称点 $C$ 的坐标为；

(3)、在平面直角坐标系中标出点B，C所在位置，并求出四边形OBAC的面积.

查看试题解析
22. 在△ABC中， $A B = A C ， A D ⊥ B C ， E$ 为AC边上一点，过点 $B$ 作 $B F / / A C$ 交ED延长线于点 $F$ .

(1)、求证： $B F = C E$ .

(2)、连结BE，若 $E$ 是AC中点， $B F = 5 ， A D = 6$ ，求BE的长.

查看试题解析
23. 某中学计划购买A型和 $B$ 型课桌凳共200套，经招标，购买一套 $A$ 型课桌凳比购买一套 $B$ 型课桌凳少用40元，且购买3套 $A$ 型和5套 $B$ 型课桌凳共需1640元.

(1)、求购买一套 $A$ 型课桌凳和一套 $B$ 型课桌凳各需多少元?

(2)、学校根据实际情况，要求购买这两种课桌凳的总费用不能超过40880元，并且购买 $A$ 型课桌凳的数量不能超过 $B$ 型课桌凳数量的 $\frac{2}{3}$ ，求该校本次购买 $A$ 型和 $B$ 型课桌凳共有几种购买方案?怎样的方案使总费用最低?并求出最低消费.

查看试题解析
24. 如图1，在平面直角坐标系中， $A$ 点坐标为 $(0 ， 4) ， B$ 点坐标为 $(0 ， - 1) ， C$ 是 $x$ 轴负半轴上一点，且 $A B = A C ， P$ 是 $y$ 轴正半轴上一点，作 $P D ⊥ B C$ 于点 $D$ ，连接OD.

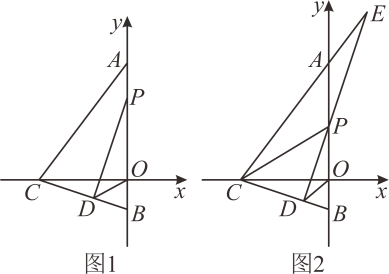(1)、C点坐标为， $B C =$ .

(2)、①当点 $P$ 在线段OA上时，若 $△ O B D$ 是以OB为腰的等腰三角形，请求出所有符合条件的 $P$ 点坐标.
②如图2，设DP交直线AC于点 $E$ ，连结CP，若 $S_{△ A C P} ： S_{△ A E P} = 5 ： 2$ ，则 $S_{△ C O P} =$ (直接写出结果).

查看试题解析