浙江省瑞安市2023-2024学年八年级第一学期数学期中试卷
试卷更新日期:2023-12-21 类型:期中考试
一、选择题(本题有10小题,每小题3分,共30分,每小题只有一个选项是正确的,不选、多选、错选,均不给分)
-
1. 下列长度(单位cm)的线段不能组成三角形的是( )A、3,3,3 B、3,5,5 C、3,4,5 D、3,5,82. 下列各组图形中是全等三角形的一组是( )A、
 B、
B、 C、
C、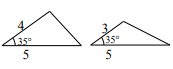 D、
D、 3. 对于命题“如果与互补,那么”,能说明这个命题是假命题的反例是( )A、 , B、 , C、 , D、 ,4. 将一副三角板按如图所示的方式放置,则∠α的度数为( )
3. 对于命题“如果与互补,那么”,能说明这个命题是假命题的反例是( )A、 , B、 , C、 , D、 ,4. 将一副三角板按如图所示的方式放置,则∠α的度数为( ) A、75° B、85 C、90° D、95°5. 已知下列尺规作图:①作一个角的角平分线;②作一个角等于已知角;③作一条线段的垂直平分线,其中作法正确的是( )
A、75° B、85 C、90° D、95°5. 已知下列尺规作图:①作一个角的角平分线;②作一个角等于已知角;③作一条线段的垂直平分线,其中作法正确的是( )

 A、①③ B、①② C、②③ D、①②③6. 在△ABC中,线段AP , AQ , AR分别是BC边上的高线,中线和角平分线,则( )A、AP≤AQ B、AQ≤AR C、AP>AR D、AP>AQ7. 定理“等腰三角形的两个底角相等”的逆定理是( )A、有两个角不相等的三角形不是等腰三角形 B、不是等腰三角形的两个角不相等 C、有两个底角相等的三角形是等腰三角形 D、有两个角相等的三角形是等腰三角形8. 如图,AB , BC , CD , DE是四根长度相同的火柴棒,点A、C、E共线.若AC=12,CE=16,CD⊥BC , 则一根火柴棒的长度为( )
A、①③ B、①② C、②③ D、①②③6. 在△ABC中,线段AP , AQ , AR分别是BC边上的高线,中线和角平分线,则( )A、AP≤AQ B、AQ≤AR C、AP>AR D、AP>AQ7. 定理“等腰三角形的两个底角相等”的逆定理是( )A、有两个角不相等的三角形不是等腰三角形 B、不是等腰三角形的两个角不相等 C、有两个底角相等的三角形是等腰三角形 D、有两个角相等的三角形是等腰三角形8. 如图,AB , BC , CD , DE是四根长度相同的火柴棒,点A、C、E共线.若AC=12,CE=16,CD⊥BC , 则一根火柴棒的长度为( ) A、8 B、10 C、12 D、149. 如图,在Rt△ABC中,∠BAC=90°,∠C=30°,将边AB沿着AE翻折,使点B落在BC上的点D处,再将边AC沿着AF翻折,使得C落在AD延长线上的点C′处,两条折痕与斜边BC分别交于E , F . 以下四个结论正确的是( )
A、8 B、10 C、12 D、149. 如图,在Rt△ABC中,∠BAC=90°,∠C=30°,将边AB沿着AE翻折,使点B落在BC上的点D处,再将边AC沿着AF翻折,使得C落在AD延长线上的点C′处,两条折痕与斜边BC分别交于E , F . 以下四个结论正确的是( )
①∠EAF=45°;②FC′=BE;③EC=3BE;④FC=(-1)AE .
A、①②③ B、②④ C、①③④ D、①②③④10. 如图,在△ABC中,点D为BC的中点,△AEF的边EF过点C,且AE=EF,AB∥EF,连结DE,DE⊥AD,S△AEC:S△ACF=3:8,AB=14,CE的值为( ) A、2.5 B、4 C、3.5 D、3
A、2.5 B、4 C、3.5 D、3二、填空题(本题有8小题,每小题3分,共24分)
-
11. 命题“两直线平行,同位角相等.”的逆命题是 .12. 若△ABC≌△DEF , A与D , B与E分别是对应顶点,∠A=50°,∠B=70°,则∠F=°.13. 在等腰三角形中,若 , 则(用“>”“=”“<”中的一个符号填空).14. 如图,已知P是∠ABC平分线BD上一点,PE⊥BC , PF⊥BA , 垂足分别是E、F , 如果PE=3,那么PF= .
 15. 如图,一太阳能热水器支架(Rt△ACB)两直角边AC=1.2米,CB=1.6米,点D为受光面斜边AB的中点,则连杆CD的长为米.
15. 如图,一太阳能热水器支架(Rt△ACB)两直角边AC=1.2米,CB=1.6米,点D为受光面斜边AB的中点,则连杆CD的长为米.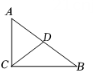 16. 如图,在△ABC中,AB=AC , D为BC上的一点,∠BAD=30°,在AD的右侧作△ADE , 使得AE=AD , ∠DAE=∠BAC , 连接CE , DE , DE交AC于点O , 若CE∥AD , 则∠DOC的度数为 .
16. 如图,在△ABC中,AB=AC , D为BC上的一点,∠BAD=30°,在AD的右侧作△ADE , 使得AE=AD , ∠DAE=∠BAC , 连接CE , DE , DE交AC于点O , 若CE∥AD , 则∠DOC的度数为 . 17. 由沈康身教授所著,数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事:如图,三姐妹为了平分一块边长为1的祖传正方形地毯,先将地毯分割成七块,再拼成三个小正方形(阴影部分).则图中AB的长应是 .
17. 由沈康身教授所著,数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事:如图,三姐妹为了平分一块边长为1的祖传正方形地毯,先将地毯分割成七块,再拼成三个小正方形(阴影部分).则图中AB的长应是 .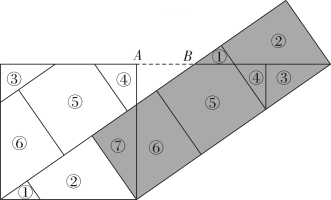 18. 如图,点P是在正△ABC内一点.PA=6,PB=8,PC=10,将线段AP绕点A逆时针旋转60°得到线段AP′ , 连结.P′P , P′C , 四边形APCP′的面积为 , S△APB+S△BPC= .
18. 如图,点P是在正△ABC内一点.PA=6,PB=8,PC=10,将线段AP绕点A逆时针旋转60°得到线段AP′ , 连结.P′P , P′C , 四边形APCP′的面积为 , S△APB+S△BPC= .
三、解答题(本题有5小题,共46分,解答需写出必要的文字说明、演算步骤或证明过程)
-
19. 如图,在△ABC中,点D在BC边上,AB=AD=CD . 若∠BAD=36°,求∠C的度数.
 20. 如图,AB∥CD , AB=CD , 点E和点F在线段BC上,∠A=∠D .
20. 如图,AB∥CD , AB=CD , 点E和点F在线段BC上,∠A=∠D . (1)、求证:AE=DF .(2)、若BC=16,EF=6,求BE的长.21. 如图,在△ABC中,∠BAC=90°,AB=AC , D是AC边上一点,连接BD , EC⊥AC , 且AE=BD , AE与BC交于点F .
(1)、求证:AE=DF .(2)、若BC=16,EF=6,求BE的长.21. 如图,在△ABC中,∠BAC=90°,AB=AC , D是AC边上一点,连接BD , EC⊥AC , 且AE=BD , AE与BC交于点F . (1)、求证:CE=AD .(2)、当AD=CF时,求证:BD平分∠ABC .22. 如图,在等腰△ABC中,AB=AC , BD⊥AC于点D , 已知BD=6,AD=8.
(1)、求证:CE=AD .(2)、当AD=CF时,求证:BD平分∠ABC .22. 如图,在等腰△ABC中,AB=AC , BD⊥AC于点D , 已知BD=6,AD=8.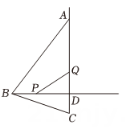 (1)、求CD的长.(2)、动点P从点B出发,沿射线BD以每秒1个单位长度的速度运动,Q为射线DA上一点,DQ=BP , 连结PQ , 设点P运动的时间为t秒.
(1)、求CD的长.(2)、动点P从点B出发,沿射线BD以每秒1个单位长度的速度运动,Q为射线DA上一点,DQ=BP , 连结PQ , 设点P运动的时间为t秒.①当点P在线段BD上时,若△CPQ是以CP为腰的等腰三角形,求t的值.
②在点P的整个运动过程中,作点Q关于AP的对称点 , 连结 , 当//AC时,请直接写出此时PD的长: ▲ .
23. 如图,△ABC和△ADC都是等腰直角三角形,∠ABC=∠ADC=90°,点E,F分别在射线BA,BC上,DE⊥DF,点M为EF的中点,点P在BC上,BP=2,CP=6, (1)、当点E在BA的延长线上,证明AE=CF.(2)、当△MPF为直角三角形,求AE的长.(3)、直接写出PM的最小值 .
(1)、当点E在BA的延长线上,证明AE=CF.(2)、当△MPF为直角三角形,求AE的长.(3)、直接写出PM的最小值 .