浙江省杭州市萧山区2023年九年级上学期数学期中试卷2
试卷更新日期:2023-12-20 类型:期中考试
一、选择题:本大题有10个小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 下列事件为必然事件的是( )A、购买两张彩票,一定中奖 B、打开电视,正在播放新闻联播 C、抛掷一枚硬币,正面向上 D、三角形三个内角和为180°2. 二次函数y=-2(x-1)2+2的顶点坐标是( )A、(1,2) B、(-1,2) C、(1,-2) D、(-1,-2)3. 如图,△AOB绕点O逆时针旋转65°得到△COD,若∠COD=30°,则∠BOC的度数是( )
 A、30° B、35° C、45° D、65°4. 一条排水管的截面如图所示, 已知排水管的半径 , 水面宽 , 则截面圆心O到水面的距离是( )
A、30° B、35° C、45° D、65°4. 一条排水管的截面如图所示, 已知排水管的半径 , 水面宽 , 则截面圆心O到水面的距离是( ) A、4 B、3 C、2 D、15. 下列命题中,正确的命题是( )A、三角形的外心是三角形三边中垂线的交点 B、三点确定一个圆 C、平分一条弦的直径一定垂直于弦 D、相等的两个圆心角所对的两条弧相等6. 已知抛物线过点 , 则的值为( )A、0 B、1 C、2 D、37. 大数据分析技术为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的健康码(绿码)示意图,用黑白打印机打印于边长为 的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量反复实验,发现点落入黑色部分的频率稳定在 左右,据此可以估计黑色部分的总面积约为( )
A、4 B、3 C、2 D、15. 下列命题中,正确的命题是( )A、三角形的外心是三角形三边中垂线的交点 B、三点确定一个圆 C、平分一条弦的直径一定垂直于弦 D、相等的两个圆心角所对的两条弧相等6. 已知抛物线过点 , 则的值为( )A、0 B、1 C、2 D、37. 大数据分析技术为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的健康码(绿码)示意图,用黑白打印机打印于边长为 的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量反复实验,发现点落入黑色部分的频率稳定在 左右,据此可以估计黑色部分的总面积约为( )
 A、 B、 C、 D、8. 如图,二次函数y=ax2+bx+c的图象的对称轴为x=- , 且经过点(-2,0),(x1 , y1),(x2 , y2),下列说法正确的是( )
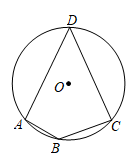
A、 B、 C、 D、8. 如图,二次函数y=ax2+bx+c的图象的对称轴为x=- , 且经过点(-2,0),(x1 , y1),(x2 , y2),下列说法正确的是( ) A、bc>0 B、当x1>x2≥-时,y1>y2 C、a=2b D、不等式ax2+bx+c<0的解集是-2<x<9. 如图,在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连接CD.若点D与圆心O不重合,∠BAC=26°,则∠DCA的度数为( )
A、bc>0 B、当x1>x2≥-时,y1>y2 C、a=2b D、不等式ax2+bx+c<0的解集是-2<x<9. 如图,在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连接CD.若点D与圆心O不重合,∠BAC=26°,则∠DCA的度数为( ) A、36° B、38° C、40° D、42°10. 已知一个二次函数图象经过P1(﹣3,y1),P2(﹣1,y2),P3(1,y3),P4(3,y4)四点,若y3<y2<y4 , 则y1 , y2 , y3 , y4的最值情况是( )A、y3最小,y1最大 B、y3最小,y4最大 C、y1最小,y4最大 D、无法确定
A、36° B、38° C、40° D、42°10. 已知一个二次函数图象经过P1(﹣3,y1),P2(﹣1,y2),P3(1,y3),P4(3,y4)四点,若y3<y2<y4 , 则y1 , y2 , y3 , y4的最值情况是( )A、y3最小,y1最大 B、y3最小,y4最大 C、y1最小,y4最大 D、无法确定二、填空题:本大题有6个小题,每小题4分,共24分。
-
11. 正六边形一个内角的度数是°.12. 已知二次函数y=3(x-3)(x+2),则该函数对称轴为直线 .13. 如图,的内接四边形中, , 则的度数为.
 14. 如图所示的网格由边长均为1的小正方形组成,点A、B、C、D、E、F在小正方形的顶点上,则外接圆的圆心是点 , 弧的长是.
14. 如图所示的网格由边长均为1的小正方形组成,点A、B、C、D、E、F在小正方形的顶点上,则外接圆的圆心是点 , 弧的长是.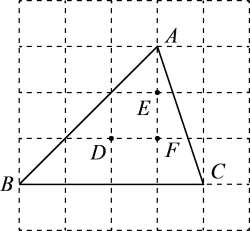 15. 已知点P(-3,m)和Q(1,m)在二次函数y=2x2+bx-1的图象上.将这个二次函数图象向上平移单位长度后,得到的函数图象与x轴只有一个公共点.16. 定义:在平面内,一个点到图形的距离是这个点到这个图上所有点的最短距离.如图,在平面内有一个正方形,边长为3,中心为O,在正方形外有一点P,OP=3,当正方形绕着点O旋转时,则点P到正方形的最短距离d的取值范围为 .
15. 已知点P(-3,m)和Q(1,m)在二次函数y=2x2+bx-1的图象上.将这个二次函数图象向上平移单位长度后,得到的函数图象与x轴只有一个公共点.16. 定义:在平面内,一个点到图形的距离是这个点到这个图上所有点的最短距离.如图,在平面内有一个正方形,边长为3,中心为O,在正方形外有一点P,OP=3,当正方形绕着点O旋转时,则点P到正方形的最短距离d的取值范围为 .
三、解答题:本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤。
-
17. 已知二次函数y=a(x-1)2-3(a≠0)的图象经过点(2,0).(1)、求a的值.(2)、求二次函数图象与x轴的交点坐标.18. 一个不透明的袋中装有2个白球,3个黑球,5个红球,每个球除颜色外都相同.(1)、从中任意摸出一个球,摸到红球是事件;摸到黄球是事件;(填“不可能”或“必然”或“随机”)(2)、从中任意摸出一个球,摸到黑球的概率;(3)、现在再将若干个同样的黑球放入袋中、与原来10个球均匀混合在一起,使从袋中任意摸出一个球为黑球的概率为 , 请求出后来放入袋中的黑球个数.19. 如图所示,以▱ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E,F,延长BA交⊙A于点G.
 (1)、求证:;(2)、若∠C=120°,BG=4,求阴影部分弓形的面积.20. 四张卡片上分别标有1,2,3,4,它们除数字外没有区别,现将它们放在不透明的盒子里搅拌均匀,任意从盒子里抽取一张卡片,不放回,再任意抽取第二张卡片.(1)、请用画树状图或列表的方式求出抽取的两张卡片数字和大于等于5的概率;(2)、若取出的两张卡片上的数字都为奇数,则甲胜;取出的两张卡片上的数字为一奇一偶,则乙胜;试分析这个游戏是否公平?请说明理由.21. 杭州某地种植有机蔬菜,已知某种蔬菜的销售单价y(元)与销售月份x之间的关系满足y=-x+9,每千克成本z(元)与销售月份x之间的关系如图所示,图象为抛物线,其最低点坐标是(6,1).(其中x是满足1≤x≤12的整数)
(1)、求证:;(2)、若∠C=120°,BG=4,求阴影部分弓形的面积.20. 四张卡片上分别标有1,2,3,4,它们除数字外没有区别,现将它们放在不透明的盒子里搅拌均匀,任意从盒子里抽取一张卡片,不放回,再任意抽取第二张卡片.(1)、请用画树状图或列表的方式求出抽取的两张卡片数字和大于等于5的概率;(2)、若取出的两张卡片上的数字都为奇数,则甲胜;取出的两张卡片上的数字为一奇一偶,则乙胜;试分析这个游戏是否公平?请说明理由.21. 杭州某地种植有机蔬菜,已知某种蔬菜的销售单价y(元)与销售月份x之间的关系满足y=-x+9,每千克成本z(元)与销售月份x之间的关系如图所示,图象为抛物线,其最低点坐标是(6,1).(其中x是满足1≤x≤12的整数) (1)、问:2月份每千克蔬菜成本是多少?(2)、判断哪个月份销售每千克蔬菜的收益最大?并求最大收益.
(1)、问:2月份每千克蔬菜成本是多少?(2)、判断哪个月份销售每千克蔬菜的收益最大?并求最大收益.
